Skip to main content
Engineering LibreTexts

5.8: Exercises

  1. Last updated
  2. Save as PDF
  • Page ID
    46133

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    1. A connector used in a \(50\:\Omega\) system introduces a series resistance of \(0.5\:\Omega\). What is the insertion loss of the connector?
    2. A microwave switch is used in a \(75\:\Omega\) system and has a \(5\:\Omega\) on resistance. The reactive parasitics of the switch are negligible.
      1. What is the insertion loss of the switch in the on state?
      2. What is the return loss of the switch in the on state?
    3. A microwave switch is used in a \(50\:\Omega\) system and has a \(5\:\Omega\) on resistance. The reactive parasitics of the switch are negligible.
      1. What is the insertion loss of the switch in the on state?
      2. If the available power of the source is \(50\text{ W}\), what is the power dissipated by the switch?
    4. A microwave switch is used at \(1\text{ GHz}\) in a \(50\:\Omega\) system and it has a \(2\:\Omega\) on resistance and a \(2\text{ k}\Omega\) off resistance. The reactive parasitics of the switch are negligible.
      1. What is the insertion loss of the switch?
      2. What is the isolation of the switch (i.e., what is the insertion loss of the switch when it is in the off state)?
    5. A microwave switch is used at \(1\text{ GHz}\) in a \(50\:\Omega\) system. The switch has a \(0.5\:\Omega\) on resistance, a \(2\text{ k}\Omega\) off resistance, and a parasitic capacitance between the input and output of the switch of \(1\text{ pF}\) when the switch is in the off state. Other reactive parasitics of the switch are negligible.
      1. What is the insertion loss of the switch?
      2. What is the isolation of the switch ignoring the capacitance of the switch in the off state (i.e., what is the insertion loss of the switch when it is in the off state)?
      3. What is the isolation of the switch with the off capacitance included?
    6. Consider a microwave switch used in a \(50\:\Omega\) system. The switch has a \(0.5\:\Omega\) on resistance, a \(1\text{ k}\Omega\) off resistance, and a \(0.1\text{ pF}\) off capacitance. Other reactive parasitics of the switch are negligible.
      1. What is the insertion loss of the switch at \(1\text{ GHz}\)?
      2. What is the isolation of the switch at \(1\text{ GHz}\) (i.e., what is the insertion loss of the switch when it is in the off state)?
      3. What is the insertion loss at \(10\text{ GHz}\)?
      4. What is the isolation at \(10\text{ GHz}\)?
      5. What is the return loss of the switch at \(1\text{ GHz}\) when the switch is in the on state?
    7. A microwave switch has a \(5\:\Omega\) on resistance, and an off resistance of \(500\:\Omega\). The reactive parasitics of the switch are negligible.
      1. What is the insertion loss of the switch when it is used in a \(50\:\Omega\) system?
      2. What is the insertion loss of the switch when it is used in a \(100\:\Omega\) system?
      3. What is the isolation of the switch when it is used in a \(50\:\Omega\) system? (That is, what is the insertion loss of the switch when it is in the off state?)
      4. What is the isolation of the switch when it is used in a \(100\:\Omega\) system?
    8. The RF front end of a communications unit consists of a switch, then an amplifier, and then a mixer. The switch has a loss of \(0.5\text{ dB}\), the amplifier has a gain of \(20\text{ dB}\), and the mixer has a conversion gain of \(3\text{ dB}\). What is the overall gain of the cascade?
    9. Using a schematic, show how an isolator can be obtained from a circulator.
    10. A three-port circulator has the \(S\) parameters
      \[\left[\begin{array}{ccc}{0}&{0}&{1}\\{1}&{0}&{0}\\{0}&{1}&{0}\end{array}\right]\nonumber \]
      If port 3 is terminated in a matched load to create a two-port network
      1. What is the name given to this network?
      2. Write down the \(S\) parameters of the two-port?
    11. A three-port circulator has the \(S\) parameters
      \[\left[\begin{array}{ccc}{0}&{0}&{0.5}\\{20.5}&{0}&{0}\\{0}&{0.5}&{0}\end{array}\right]\nonumber \]
      Port \(\mathsf{3}\) is terminated in a matched load creating a two-port network.
      1. Find the \(S\) parameters of the two-port.
      2. What is the return loss in \(\text{dB}\) at Port \(\mathsf{1}\) if Port \(\mathsf{2}\) is terminated in a matched load?
      3. What is the insertion loss in \(\text{dB}\) for a signal applied at Port \(\mathsf{1}\) and leaving at Port \(\mathsf{2}\) with matched source and load impedances?
      4. What is the insertion loss in \(\text{dB}\) for a signal applied at Port \(\mathsf{2}\) and leaving at Port \(\mathsf{1}\) with matched source and load impedances?
    12. A three-port circulator in a \(75-\Omega\) system has the \(S\) parameters
      \[\left[\begin{array}{ccc}{0.1}&{0}&{0.707}\\{0.707}&{0.1}&{0}\\{0}&{0.707}&{0.1}\end{array}\right]\nonumber \]
      Port \(\mathsf{3}\) is terminated in \(75-\Omega\) creating a two-port network.
      1. Find the \(S\) parameters of the two-port.
      2. What is the return loss in \(\text{dB}\) at Port \(\mathsf{1}\) if Port \(\mathsf{2}\) is terminated in \(75-\Omega\)?
      3. What is the insertion loss in \(\text{dB}\) for a signal applied at Port \(\mathsf{1}\) and leaving at Port \(\mathsf{2}\) with \(75-\Omega\) source and load impedances?
      4. What is the insertion loss in dB for a signal applied at Port \(\mathsf{2}\) and leaving at Port \(\mathsf{1}\) with \(75-\Omega\) source and load impedances?
    13. A three-port circulator has the \(S\) parameters
      \[\left[\begin{array}{ccc}{0}&{1}&{0}\\{0}&{0}&{1}\\{1}&{0}&{0}\end{array}\right]\nonumber \]
      1. In no more than \(50\) words describe the function of a circulator?
      2. Describe power flow for the circulator with the given \(S\) parameters. When power enters one of ports, at which port does power leave? Consider power entering Port \(1\), then Port \(2\), then Port \(3\).
    14. An ideal three-port circulator in a \(50\:\Omega\) system is configured as an isolator from Port \(\mathsf{1}\) to Port \(\mathsf{2}\). The termination at the third port of the circulator has a value of \(45\:\Omega\). What is the isolation of the isolator? (This is the insertion loss in the reverse direction.) [Hint: Use signal flow graph analysis.]
    15. Two isolators are used in cascade. Each isolator has an isolation of \(20\text{ dB}\). The isolators are matched so that their input and output reflection coefficients are zero. Determine the isolation of the cascaded isolator system?
    16. A three-port circulator in a \(50-\Omega\) system has the \(S\) parameters
      \[\left[\begin{array}{ccc}{0.1}&{0.01}&{0.5}\\{0.5}&{0.1}&{0.01}\\{0.01}&{0.5}&{0.1}\end{array}\right]\nonumber \]
      If port \(3\) is terminated in a matched load to create a two-port network
      1. Find the \(S\) parameters of the two-port.
      2. What is the return loss in \(\text{dB}\) at Port \(\mathsf{1}\) if Port \(\mathsf{2}\) is terminated in \(50-\Omega\)?
      3. What is the insertion loss in \(\text{dB}\) for a signal applied at Port \(\mathsf{2}\) and leaving at Port \(\mathsf{1}\) with \(50-\Omega\) source and load impedances?
      4. What is the insertion loss in \(\text{dB}\) for a signal applied at Port \(\mathsf{1}\) and leaving at Port \(\mathsf{2}\) with \(50-\Omega\) source and load impedances?
      5. What is is the name of this network?
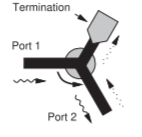
    17. Write down the two-port \(S\) parameters of the microstrip isolator shown below.

    clipboard_eb6b95c2216b77d394e4dc27fc4cfe4ec.png

    5.8.1 Exercises By Section

    \(†\)challenging, \(‡\)very challenging

    \(§5.4\: 1, 2†, 3†, 4†, 5†, 6†, 7†\)

    \(§5.5\: 10, 11, 12, 13, 14†, 15, 16, 17\)

    5.8.2 Answers to Selected Exercises

    1. (b) \(29.8\text{ dB}\)
    2. (a) \(0.424\text{ dB}\)
    1. (c) \(5.76\text{ dB}\)
    1. \(0.424\text{ dB}\)
    2. \(22.5\text{ dB}\)
    1. \(40\text{ dB}\)

    5.8: Exercises is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
    2. Tags
      This page has no tags.