Skip to main content
Engineering LibreTexts

9.5: Exercises

  1. Last updated
  2. Save as PDF
  • Page ID
    25442

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\dsum}{\displaystyle\sum\limits} \)

    \( \newcommand{\dint}{\displaystyle\int\limits} \)

    \( \newcommand{\dlim}{\displaystyle\lim\limits} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \(\newcommand{\longvect}{\overrightarrow}\)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\ket}[1]{\left| #1 \right>}\)
    \(\newcommand{\bra}[1]{\left< #1 \right|}\)
    \(\newcommand{\braket}[2]{\left< #1 \vphantom{#2} \right| \left. #2 \vphantom{#1} \right>}\)
    \(\newcommand{\braopket}[3]{\left< #1 \vphantom{#2}\vphantom{#3} \right| #2 \vphantom{#1}\vphantom{#3} \left| #3 \vphantom{#1}\vphantom{#2} \right>}\)
    \(\newcommand{\qmvec}[1]{\mathbf{\vec{#1}}}\)
    \(\newcommand{\op}[1]{\hat{\mathbf{#1}}}\)
    \(\newcommand{\expect}[1]{\langle #1 \rangle}\)
    \(\newcommand{\dfn}[1]{\emph{\textbf{#1}}}\)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    9.5.1: Analysis Problems

    1. For the circuit of Figure \(\PageIndex{1}\), determine compliance, \(P_{load(max)}\), \(P_{D(max)}\), \(BV_{CEO}\) and \(I_{C(max)}\). \(V_{CC}\) = 15 V, \(V_{EE}\) = −15 V, \(\beta\) = 75, \(R_L\) = 16 \(\Omega\), \(R_1\) = 680 \(\Omega\), \(R_2\) = 680 \(\Omega\).

    2. For the circuit of Figure \(\PageIndex{1}\), determine \(Z_{in}\). \(V_{CC}\) = 15 V, \(V_{EE}\) = −15 V, \(\beta\) = 75, \(R_L\) = 16 \(\Omega\), \(R_1\) = 680 \(\Omega\), \(R_2\) = 680 \(\Omega\).

    3. For the circuit of Figure \(\PageIndex{1}\), determine \(Z_{in}\). \(V_{CC}\) = 25 V, \(V_{EE}\) = −25 V, \(\beta\) = 70, \(R_L\) = 8 \(\Omega\), \(R_1\) = 560 \(\Omega\), \(R_2\) = 560 \(\Omega\).

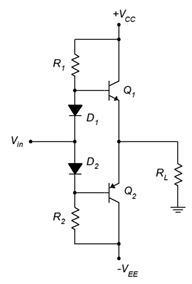
    clipboard_e28bfdd44f5cf0b81b84c7e750df840eb.png

    Figure \(\PageIndex{1}\)

    4. For the circuit of Figure \(\PageIndex{1}\), determine compliance \(P_{load(max)}\), \(P_{D(max)}\), \(BV_{CEO}\) and \(I_{C(max)}\). \(V_{CC}\) = 25 V, \(V_{EE}\) = −25 V, \(\beta\) = 70, \(R_L\) = 8 \(\Omega\), \(R_1\) = 560 \(\Omega\), \(R_2\) = 560 \(\Omega\).

    5. For the circuit of Figure \(\PageIndex{2}\), determine \(P_{load(max)}\), \(P_{D(max)}\), \(BV_{CEO}\) and \(I_{C(max)}\). \(V_{CC}\) = 15 V, \(\beta\) = 75, \(R_L\) = 16 \(\Omega\), \(R_1\) = 630 \(\Omega\), \(R_2\) = 630 \(\Omega\).

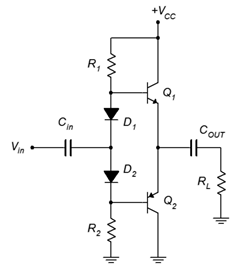
    clipboard_ebd403ecd859615415b3e6771164be1d4.png

    Figure \(\PageIndex{2}\)

    6. For the circuit of Figure \(\PageIndex{2}\), determine \(Z_{in}\). \(V_{CC}\) = 15 V, \(\beta\) = 75, \(R_L\) = 16 \(\Omega\), \(R_1\) = 630 \(\Omega\), \(R_2\) = 630 \(\Omega\).

    7. For the circuit of Figure \(\PageIndex{2}\), determine \(Z_{in}\). \(V_{CC}\) = 25 V, \(\beta\) = 70, \(R_L\) = 8 \(\Omega\), \(R_1\) = 560 \(\Omega\), \(R_2\) = 560 \(\Omega\).

    8. For the circuit of Figure \(\PageIndex{2}\), determine \(P_{load(max)}\), \(P_{D(max)}\), \(BV_{CEO}\) and \(I_{C(max)}\). \(V_{CC}\) = 25 V, \(\beta\) = 70, \(R_L\) = 8 \(\Omega\), \(R_1\) = 510 \(\Omega\), \(R_2\) = 510 \(\Omega\).

    9. For the circuit of Figure \(\PageIndex{3}\), determine \(P_{load(max)}\), \(P_{D(max)}\), \(BV_{CEO}\) and \(I_{C(max)}\) for the output transistors. \(V_{CC}\) = 24 V, \(V_{EE}\) = −24 V, \(\beta\) = 75, \(R_L\) = 8 \(\Omega\), \(R_1\) = 2.5 k\(\Omega\), \(R_2\) = 300 \(\Omega\), \(R_3\) = 330 \(\Omega\), \(R_4\) = 63 \(\Omega\).

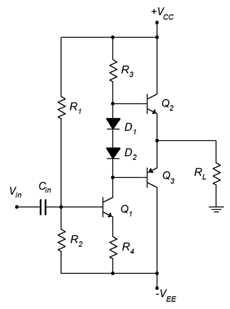
    clipboard_ec9a6f67a4320c2aa3903279b4e08ce21.png

    Figure \(\PageIndex{3}\)

    10. For the circuit of Figure \(\PageIndex{3}\), determine \(A_v\) and \(Z_{in}\). \(V_{CC}\) = 24 V, \(V_{EE}\) = −24 V, \(\beta\) = 75, \(R_L\) = 8 \(\Omega\), \(R_1\) = 2.5 k\(\Omega\), \(R_2\) = 300 \(\Omega\), \(R_3\) = 330 \(\Omega\), \(R_4\) = 63 \(\Omega\).

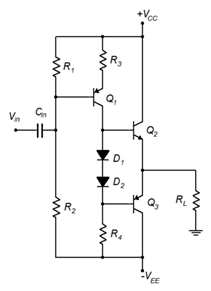
    clipboard_e4ab318a3f54e3e72eb40b490f42b2f88.png

    Figure \(\PageIndex{4}\)

    11. For the circuit of Figure \(\PageIndex{4}\), determine \(P_{load(max)}\), \(P_{D(max)}\), \(BV_{CEO}\) and \(I_{C(max)}\) for the output transistors. \(V_{CC}\) = 24 V, \(V_{EE}\) = −24 V, \(\beta\) = 75, \(R_L\) = 16 \(\Omega\), \(R_1\) = 600 \(\Omega\), \(R_2\) = 5 k\(\Omega\), \(R_3\) = 63 \(\Omega\), \(R_4\) = 330 \(\Omega\).

    12. For the circuit of Figure \(\PageIndex{4}\), determine \(A_v\) and \(Z_{in}\). \(V_{CC}\) = 24 V, \(V_{EE}\) = −24 V, \(\beta\) = 75, \(R_L\) = 16 \(\Omega\), \(R_1\) = 600 \(\Omega\), \(R_2\) = 5 k\(\Omega\), \(R_3\) = 63 \(\Omega\), \(R_4\) = 330 \(\Omega\).

    13. Determine the limit current for the circuit of Figure \(\PageIndex{5}\) if \(R_E\) = 0.2 \(\Omega\).

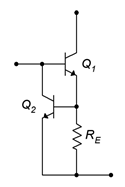
    clipboard_ea05cc0428246990f4b6be75b676a6c3f.png

    Figure \(\PageIndex{5}\)

    14. Determine \(P_{load(max)}\), and \(P_{D(max)}\), \(BV_{CEO}\) and \(I_{C(max)}\) for the output and driver transistors of Figure \(\PageIndex{6}\). \(V_{CC}\) = 50 V, \(V_{EE}\) = −50 V, \(\beta\) = 75, \(R_L\) = 8 \(\Omega\), \(R_5\) through \(R_8\) = 0.05 \(\Omega\). Assume all other components produce proper bias.

    9.5.2: Design Problems

    15. For the circuit of Figure \(\PageIndex{3}\), determine values for \(R_1\) and \(R_2\) for proper bias. \(V_{CC}\) = 32 V, \(V_{EE}\) = −32 V, \(\beta\) = 75, \(R_L\) = 8 \(\Omega\), \(R_3\) = 330 \(\Omega\), \(R_4\) = 63 \(\Omega\).

    16. Determine a value for \(R_E\) to set the limit current for the circuit of Figure \(\PageIndex{5}\) to 2 A.

    9.5.3: Challenge Problems

    17. For the circuit of Figure \(\PageIndex{6}\), determine values for \(R_1\) and \(R_2\) for proper bias. \(V_{CC}\) = 50 V, \(V_{EE}\) = −50 V, \(\beta\) = 85, \(R_L\) = 8 \(\Omega\), \(R_5\) through \(R_8\) = 0.05 \(\Omega\), \(R_3\) = 2.2 k\(\Omega\), \(R_4\) = 330 \(\Omega\).

    18. For the circuit of Figure \(\PageIndex{7}\), determine a value for \(R_5\) for proper bias. \(V_{CC}\) = 30 V, \(V_{EE}\) = −30 V, \(\beta\) = 100, \(R_L\) = 16 \(\Omega\), \(R_1\) = 2.2 k\(\Omega\), \(R_2\) = 8.2 k\(\Omega\), \(R_3\) = 1.2 k\(\Omega\), \(R_4\) = 47 \(\Omega\), \(R_5\) = 330 \(\Omega\), \(R_6\) = 470 \(\Omega\), \(R_7\) = 68 \(\Omega\).

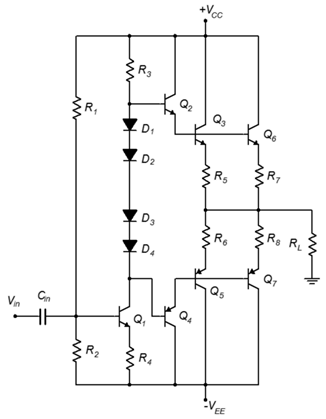
    clipboard_e1109d25b4efdbd532553b3e8385eb199.png

    Figure \(\PageIndex{6}\)

    9.5.4: Computer Simulation Problems

    19. Perform a transient analysis on the circuit of Problem 1 to verify the compliance.

    20. Perform a transient analysis on the circuit of Problem 4 to verify the compliance.

    21. Perform a DC analysis on the design from Problem 15 to verify the results.

    22. Perform a DC analysis on the design from Problem 17 to verify the results.

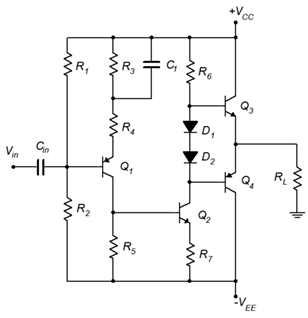
    clipboard_ebbb452bafae974e1f76c2abc2b1c4e64.png

    Figure \(\PageIndex{7}\)

    This page titled 9.5: Exercises was last modified on Mon, 22 Mar 2021 03:00:59 GMT and is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by James M. Fiore via source content that was edited to the style and standards of the LibreTexts platform.