13.3: MOSFET Common Drain Followers
- Page ID
- 25335
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)As discussed under the section on JFETs, the common drain amplifier is also known as the source follower. The prototype amplifier circuit with device model is shown in Figure \(\PageIndex{1}\). As with all voltage followers, we expect a non-inverting voltage gain close to unity with a high \(Z_{in}\) and a low \(Z_{out}\).
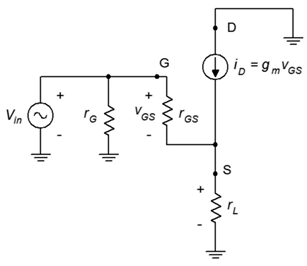
Figure \(\PageIndex{1}\): Common drain (source follower) prototype.
As is usual, the input signal is applied to the gate terminal and the output is taken from the source. Because the output is at the source, biasing schemes that have the source terminal grounded, such as zero bias and voltage divider bias, cannot be used.
13.3.1: Voltage Gain
The voltage gain equation for the common drain follower is developed as follows: We begin with the fundamental definition that voltage gain is the ratio of \(v_{out}\) to \(v_{in}\), and proceed by expressing these voltages in terms of their Ohm's law equivalents. The load is now located at the MOSFET's source, and thus can be referred to as either \(r_L\) or \(r_S\).
\[A_v = \frac{v_{out}}{v_{i n}} = \frac{v_S}{v_G} = \frac{v_L}{v_G} \\ A_v = \frac{i_D r_L}{i_D r_L+v_{GS}} \\ A_v = \frac{g_m v_{GS} r_L}{g_m v_{GS} r_L+v_{GS}} \\ A_v = \frac{g_m r_L}{g_m r_L+1} \label{13.5} \]
or, if preferred
\[A_v = \frac{g_m r_S}{g_m r_S+1} \label{13.5b} \]
If \(g_mr_S \gg 1\), the voltage gain will be very close to unity; a desired outcome.
13.3.2: Input Impedance
The analysis for source follower's input impedance is virtually identical to that for the common source amplifier. The same commentary applies regarding the simplification of gate biasing resistors to arrive at the value of \(r_G\).
\[Z_{in} = r_G || r_{GS} \approx r_G \label{13.6} \]
13.3.3: Output Impedance
In order to determine the output impedance, we modify the circuit of Figure \(\PageIndex{1}\) by separating the load resistance from the source bias resistor. This is shown in Figure \(\PageIndex{2}\).
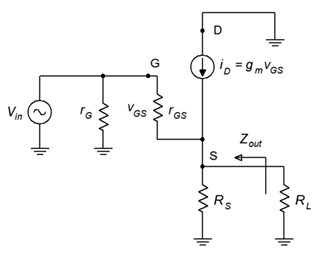
Figure \(\PageIndex{2}\): Source follower output impedance analysis.
Looking back into the source from the perspective of the load we find that the source biasing resistor, \(R_S\), is in parallel with the impedance looking back into the source terminal.
\[Z_{out} = R_S || Z_{source} \nonumber \]
To find \(Z_{source}\), note that the voltage at the source is \(v_{GS}\) and the current entering this node is \(i_D\). The ratio of the two will yield the impedance looking back into the source.
\[Z_{source} = \frac{v_{GS}}{i_D} \\ Z_{source} = \frac{v_{GS}}{g_m v_{GS}} \\ Z_{source} = \frac{1}{g_m} \label{13.7} \]
Therefore, the output impedance is
\[Z_{out} = R_S || \frac{1}{g_m} \label{13.8} \]
Looking at Equation \ref{13.8} it is obvious that the higher the transconductance, the lower the output impedance. As noted earlier, a large transconductance also means that the voltage gain will be close to unity. As a general rule then, a large transconductance is desired for the source follower.
Time for a few illustrative examples.
Example \(\PageIndex{1}\)
For the circuit of Figure \(\PageIndex{3}\), determine the voltage gain and input impedance. Assume \(V_{GS(off)}\) = −0.8 V and \(I_{DSS}\) = 30 mA.
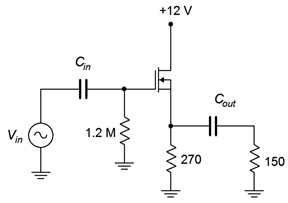
Figure \(\PageIndex{3}\): Circuit for Example \(\PageIndex{1}\).
This amplifier uses self bias so we need to determine \(g_{m0}R_S\).
\[g_{m0} =− \frac{2 I_{DSS}}{V_{GS (off )}} \nonumber \]
\[g_{m0} =− \frac{2 \times 30mA}{−0.8 V} \nonumber \]
\[g_{m0} = 75mS \nonumber \]
The DC source resistance is the 270 \(\Omega\) biasing resistor resulting in \(g_{m0} R_S\) = 16.2. From the self bias equation or graph this produces a drain current of 2.61 mA.
\[g_m = g_{m0} \sqrt{\frac{I_D}{I_{DSS}}} \nonumber \]
\[g_m = 75 mS \sqrt{\frac{2.61 mA}{30 mA}} \nonumber \]
\[g_m = 22.1mS \nonumber \]
The voltage gain is
\[A_v = \frac{g_m r_S}{g_m r_S+1} \nonumber \]
\[A_v = \frac{22.1 mS(270\Omega || 150 \Omega )}{22.1 mS \times (270 \Omega || 150\Omega ) +1} \nonumber \]
\[A_v = 0.68 \nonumber \]
Finally, for the input impedance we have
\[Z_{in} = 1.2 M\Omega || Z_{in(gate)} \approx 1.2 M\Omega \nonumber \]
Example \(\PageIndex{2}\)
For the circuit of Figure \(\PageIndex{4}\), determine the voltage gain and input impedance. Assume \(V_{GS(off)}\) = −2.5 V and \(I_{DSS}\) = 80 mA.
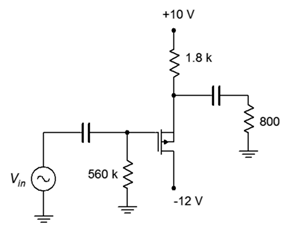
Figure \(\PageIndex{4}\): Circuit for Example \(\PageIndex{2}\).
This follower uses a P-channel device with combination bias. Note that the source terminal is toward the top of the schematic. First, determine \(g_{m0}R_S\) and the bias factor, \(k\). Then the combination bias equation can be used to determine the drain current.
\[g_{m0} =− \frac{2 I_{DSS}}{V_{GS (off )}} \nonumber \]
\[g_{m0} =− \frac{2 \times 80 mA}{−2.5 V} \nonumber \]
\[g_{m0} = 64 mS \nonumber \]
The DC source resistance is the 1.8 k\(\Omega\) biasing resistor resulting in \(g_{m0} R_S\) = 115.2. The bias factor is \(V_{SS}/V_{GS(off)}\), or 4. The combination bias equation (Equation 10.9) yields \(I_D\) = 6.67 mA.
We can now find the transconductance and voltage gain.
\[g_m = g_{m0} \sqrt{\frac{I_D}{I_{DSS}}} \nonumber \]
\[g_m = 64mS \sqrt{\frac{6.67 mA}{80mA}} \nonumber \]
\[g_m = 18.5mS \nonumber \]
The voltage gain is
\[A_v = \frac{g_m r_S}{g_m r_S+1} \nonumber \]
\[A_v = \frac{18.5 mS(1.8k \Omega || 800\Omega )}{18.5 mS \times (1.8 k\Omega || 800 \Omega ) +1} \nonumber \]
\[A_v = 0.91 \nonumber \]
Lastly, the input impedance is
\[Z_{in} = 560 k\Omega || Z_{in(gate)} \approx 560 k\Omega \nonumber \]


