7.5: Hamming Codes for Channel Coding
- Page ID
- 9993
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The idea behind Hamming codes is to intersperse, or append, extra binary digits to a binary code so that errors in transmission of the code over a channel may be detected and corrected. For example, suppose we transmit the code 01101001, and it is received as 01001001. In this transmission, the third most significant bit is received erroneously. Let's define the following “modulo-2 addition” of binary numbers:
\(\begin{gathered}
0 \oplus 0=0 \\
0 \oplus 1=1 \\
1 \oplus 0=1 \\
1 \oplus 1=0
\end{gathered}\)
Multiplication in modulo-2 arithmetic is simply \(0 \cdot 0=0 \cdot 1=1 \cdot 0=0 \text { and } 1 \cdot 1=1\). Then we can say that the error sequence 00100000 is “added” to the transmission 01101001 to produce the erroneous reception:
\(\begin{align} 01101001 & \quad transmitted \nonumber \\
\oplus \quad 00100000 & \qquad error \nonumber\\
01001001 & \quad received. \nonumber \end{align}\)
Hamming error correcting codes will permit us to receive the erroneous transmission and to detect and correct the error. This is obviously of great value in transmitting and storing information. (Imagine how upset you would be to have the binary code for your checking account confused with that of Mrs. Joan Kroc.)
Choosing the Number of Check Bits
Let's suppose we have \(N\) bits of information that we wish to transmit and that we wish to intersperse “check bits” that will enable us to detect and correct any single bit error in the transmission. If we use \(N\) information bits and nn check bits, then we will transmit a code word containing \(N+n\) bits. The \(n\) check bits can code \(2^n\) events, and we want these events to indicate whether or not any errors occurred and, if so, where they occurred. Therefore we require where \((N+n)\) is the number of single error events that can occur and +1 is the number of no-error events. For example, when \(N=4\), we require \(n=3\) so that \(2^3 \geq (4+3)+1\).
How many check bits do you require to code seven bits of information for single error correction?
Code Construction
Let's suppose we have constructed an \((N,n)\) Hamming code consisting of \(N\) information bits and \(n\) check bits (or parity bits). We denote the information bits by \(x_{1}, x_{2}, \ldots, x_{N}\) and the check bits by \(c_{1}, c_{2}, \ldots, c_{n}\). These bits may be interspersed. When \(N=4\) and \(n=3\), then a typical array of bits within a code word would be one of the following:
\(\left[\begin{array}{l}
c_{1} \\
c_{2} \\
x_{1} \\
c_{3} \\
x_{2} \\
x_{3} \\
x_{4}
\end{array}\right] \quad \text { or } \quad\left[\begin{array}{l}
x_{1} \\
x_{2} \\
x_{3} \\
x_{4} \\
c_{1} \\
c_{2} \\
c_{3}
\end{array}\right]\)
The first ordering is “natural” (as we will see), and the second is “systematic” (a term that is used to describe any code whose head is information and whose tail is check). If a single error occurs in an \((N,n)\) code, then the received code word will be the modulo-2 sum of the code word and the error word that contains a 1 in its \(i^{\text{th}}\) position:
\[\left[\begin{array}{l}
c_{1} \\
c_{2} \\
x_{1} \\
c_{3} \\
x_{2} \\
x_{3} \\
x_{4}
\end{array}\right] \oplus\left[\begin{array}{l}
0 \\
0 \\
0 \\
1 \\
0 \\
0 \\
0
\end{array}\right] \nonumber \]
We would like to operate on this received code word in such a way that the location of the error bit can be determined. If there were no code word, then an obvious solution would be to premultiply the error word by the parity check matrix
\[\begin{align}
&A^{T}=\left[\begin{array}{lllllll}
1 & 0 & 1 & 0 & 1 & 0 & 1 \\
0 & 1 & 1 & 0 & 0 & 1 & 1 \\
0 & 0 & 0 & 1 & 1 & 1 & 1
\end{array}\right]\\
& \quad [(1) \quad (2) \quad (3)\quad (4) \quad (5) \quad (6) \quad(7)] \nonumber
\end{align} \nonumber \]
The \(i^{\text{th}}\) column of \(A^T\) is just the binary code for \(i\). When \(A^T\) premultiplies an error word, the error bit picks out the column that codes the error position:
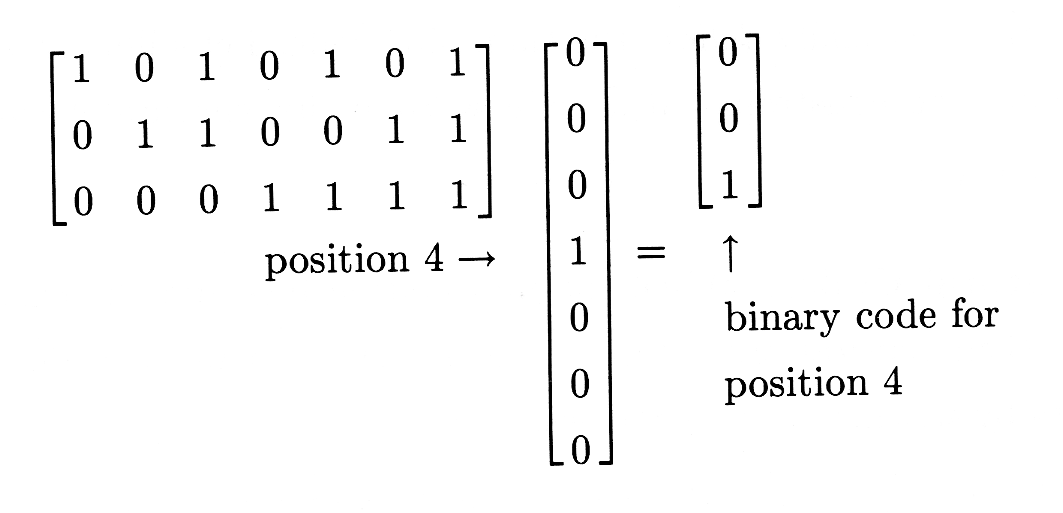
If the error word contains no error bits, then the product is 0, indicating no errors.
This seems like a good idea, but what about the effect of the code word? In Exercise 1, you are asked to show that the effect of the parity check matrix \(A^T\) applied to the modulo-2 sum of a code word \(x\) and an error word \(e\) is
\[\mathrm{A}^{T}(\mathrm{x} \oplus \mathrm{e})=\mathrm{A}^{T} \mathrm{x} \oplus \mathrm{A}^{T} \mathrm{e} \nonumber \]
In this equation all sums and products obey the rules of modulo-2 arithmetic.
Let \(y=x \oplus e\) denote the modulo-2 sum of a code word \(x\) and an error word e; \(A^T\) is a parity check matrix. Show that
\(\mathrm{A}^{T} \mathrm{y}=\mathrm{A}^{T} \mathrm{x} \oplus \mathrm{A}^{T} \mathrm{e}\)
We have designed the parity check matrix \(A^T\) so that the syndrome \(A^Te\) produces a binary code for the error location. (The location of the error is th'e syndrome for the error word.) The product \(A^Tx\) will interfere with this syndrome unless \(A^Tx\)=0. Therefore we will require that the code word \(x\) satisfy the constraint
\[\mathrm{A}^{T} \mathrm{x}=0 \nonumber \]
This constraint actually defines the Hamming code. Let's illustrate this point by applying the constraint to a code word in its “natural format" \(\mathrm{x}^{T}=\left(c_{1} c_{2} x_{1} c_{3} x_{2} x_{3} x_{4}\right)\).
Natural Codes
When the information bits and the check bits are coded in their natural order \(\left(c_{1} c_{2} x_{1} c_{3} x_{2} x_{3} x_{4}\right)\), then we may determine the check bits by writing \(A^Tx\) as follows:
\[\left[\begin{array}{lllllll}
1 & 0 & 1 & 0 & 1 & 0 & 1 \\
0 & 1 & 1 & 0 & 0 & 1 & 1 \\
0 & 0 & 0 & 1 & 1 & 1 & 1
\end{array}\right]\left[\begin{array}{l}
c_{1} \\
c_{2} \\
x_{1} \\
c_{3} \\
x_{2} \\
x_{3} \\
x_{4}
\end{array}\right]=\left[\begin{array}{l}
0 \\
0 \\
0
\end{array}\right] \nonumber \]
We use the rules of modulo-2 arithmetic to write these constraints as
\[\begin{align}
&c_{1} \oplus x_{1} \oplus x_{2} \oplus x_{4}=0 \\
&c_{2} \oplus x_{1} \oplus x_{3} \oplus x_{4}=0 \\
&c_{3} \oplus x_{2} \oplus x_{3} \oplus x_{4}=0
\end{align} \nonumber \]
Therefore the check bits \(c_1,c_2\), and \(c_3\) are simply the following modulo-2 sums
\[\begin{align}
c_{1} &=x_{1} \oplus x_{2} \oplus x_{4} \\
c_{2} &=x_{1} \oplus x_{3} \oplus x_{4} \\
c_{3} &=x_{2} \oplus x_{3} \oplus x_{4}
\end{align} \nonumber \]
This finding may be organized into the matrix equation
\[\left[\begin{array}{l}
c_{1} \\
c_{2} \\
x_{1} \\
c_{3} \\
x_{2} \\
x_{3} \\
x_{4}
\end{array}\right]=\left[\begin{array}{l}
1101 \\
1011 \\
1000 \\
0111 \\
0100 \\
0010 \\
0001
\end{array}\right]\left[\begin{array}{l}
x_{1} \\
x_{2} \\
x_{3} \\
x_{4}
\end{array}\right] . \nonumber \]
This equation shows how the code word \(x\) is built from the information bits \((x_1,x_2,x_3,x_4)\). We call the matrix that defines the construction a coder matrix and write it as \(H\):
\[x=H \Theta \nonumber \]
\[\mathrm{x}^{T}=\left(c_{1} c_{2} x_{1} c_{3} x_{2} x_{3} x_{4}\right) \quad \Theta^{T}=\left(x_{1} x_{2} x_{3} x_{4}\right) \nonumber \]
\[H=\left[\begin{array}{c}
1101 \\
1011 \\
1000 \\
0111 \\
0100 \\
0010 \\
0001
\end{array}\right] \nonumber \]
This summarizes the construction of a Hamming code \(x\).
Check to see that the product of the parity check matrix \(A^T\) and the coder matrix \(H\) is \(A^TH=0\). Interpret this result.
Fill in the following table to show what the Hamming (4,3) code is:
| \(x_1\) | \(x_2\) | \(x_3\) | \(x_4\) | \(c_1\) | \(c_2\) | \(x_1\) | \(c_3\) | \(x_2\) | \(x_3\) | \(x_4\) |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | |||||||
| 0 | 0 | 1 | 1 | |||||||
| 0 | 1 | 0 | 0 | |||||||
| 0 | 1 | 0 | 1 | |||||||
| 0 | 1 | 1 | 0 | |||||||
| 0 | 1 | 1 | 1 | |||||||
| 1 | 0 | 0 | 0 | |||||||
| 1 | 0 | 0 | 1 | |||||||
| 1 | 0 | 1 | 0 | |||||||
| 1 | 0 | 1 | 1 | |||||||
| 1 | 1 | 0 | 0 | |||||||
| 1 | 1 | 0 | 1 | |||||||
| 1 | 1 | 1 | 0 | |||||||
| 1 | 1 | 1 | 1 |
Design a Hamming \((11,n)\) code for coding eleven information bits against single errors. Show your equations for \(c_{1}, c_{2}, \ldots, c_{n}\) and write out the coder matrix \(H\) for \(x = H \Theta\)
Decoding
To decode a Hamming code, we form the syndrome \(A^Ty\) for the received (and possibly erroneous) code word \(\mathrm{y}=\mathrm{x} \oplus \mathrm{e}\). Because \(A^Tx=0\), the syndrome is
\[\mathrm{s}=\mathrm{A}^{T} \mathrm{e} \nonumber \]
Convert this binary number into its corresponding integer location and change the bit of \(y\) in that location. If the location is zero, do nothing. Now strip off the information bits. This is the decoding algorithm.
Use the table of Hamming (4,3) codes from Exercise 3 to construct a table of received codes that contain either no bit errors or exactly one bit error. Apply the decoding algorithm to construct \((x_1,x_2,x_3,x_4)\) and show that all received code words with one or fewer errors are correctly decoded.
Digital Hardware
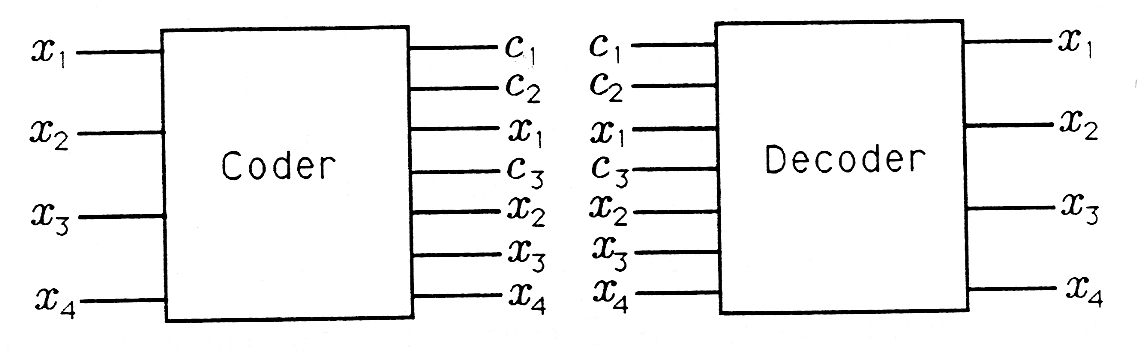
The tables you have constructed in Exercise 3 and 5 for coding and decoding Hamming (4,3) codes may be stored in digital logic chips. Their functionality is illustrated in Figure 1. The coder chip accepts \((x_1,x_2,x_3,x_4)\) as its address and generates a coded word. The decoder chip accepts \((c_1c_2x_1c_3x_2x_3x_4)\) as its address and generates a decoded word. In your courses on digital logic you will study circuits for implementing coders and decoders.
Discuss the possibility of detecting a received (4,3) code word that is neither a valid code word nor a code word with a single error. How would you use such a detector?
What fraction of received seven-bit words can be correctly decoded as Hamming (4,3) codes?
Systematic Codes
Systematic Hamming codes are codes whose information bits lead and whose check bits trail. The format for a (4,3) code is then \((x_1x_2x_3x_4c_1c_2c_3)\). The construction of a (4,3) code word from the information bits may be written as
\[\left[\begin{array}{l}
x_{1} \\
x_{2} \\
x_{3} \\
x_{4} \\
c_{1} \\
c_{2} \\
c_{3}
\end{array}\right]=\left[\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
c_{11} & c_{12} & c_{13} & c_{14} \\
c_{21} & c_{22} & c_{23} & c_{24} \\
c_{31} & c_{32} & c_{33} & c_{34}
\end{array}\right]\left[\begin{array}{c}
x_{1} \\
x_{2} \\
x_{3} \\
x_{4}
\end{array}\right] \nonumber \]
The coder matrix takes the form
\[H=\left[\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
c_{11} & c_{12} & c_{13} & c_{14} \\
c_{21} & c_{22} & c_{23} & c_{24} \\
c_{31} & c_{32} & c_{33} & c_{34}
\end{array}\right]=\left[\begin{array}{c}
I \\
c \\
c
\end{array}\right] \nonumber \]
The problem is to find the matrix \(C\) that defines the construction of check bits. The constraint \(A^Tx=0\) produces the constraint \(A^TH=0\) so that \(A^TH \Theta=0\). The constraints\(A^TH=0\) may be written out as
\[\left\{\begin{array}{lllllll}
1 & 0 & 1 & 0 & 1 & 0 & 1 \\
0 & 1 & 1 & 0 & 0 & 1 & 1 \\
0 & 0 & 0 & 1 & 1 & 1 & 1
\end{array}\right\}=\left[\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
c_{11} & c_{12} & c_{13} & c_{14} \\
c_{21} & c_{22} & c_{23} & c_{24} \\
c_{31} & c_{32} & c_{33} & c_{34}
\end{array}\right]=\left[\begin{array}{llll}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0
\end{array}\right] . \nonumber \]
These constraints produce all the equations we need (twelve equations in twelve unknowns) to determine the \(c_{ij}\).
Solve Equation 19 for the \(c_{ij}\). Show that the coder matrix for a systematic Hamming (4,3) code is
\[H=\left[\begin{array}{llll}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
0 & 1 & 1 & 1 \\
1 & 0 & 1 & 1 \\
1 & 1 & 0 & 1
\end{array}\right] \nonumber \]
Show that the coder matrix of Exercise 7 is a permutation of the coder matrix in Equation 14. (That is, the rows are reordered.)
(MATLAB) Write a MATLAB program that builds Hamming (4,3) codes from information bits \((x_1x_2x_3x_4)\) and decodes Hamming (4,3) codes \((c_1c_2x_1c_3x_2x_3x_4)\) to obtain information bits \((x_1x_2x_3x_4)\). Synthesize all seven-bit binary codes and show that your decoder correctly decodes correct codes and one-bit error codes.


