3.9: The Impedance Concept
- Page ID
- 1750
- Discussing the results if all sources in the circuit are complex exponentials.
Rather than solving the differential equation that arises in circuits containing capacitors and inductors, let's pretend that all sources in the circuit are complex exponentials having the same frequency. Although this pretense can only be mathematically true, this fiction will greatly ease solving the circuit no matter what the source really is.
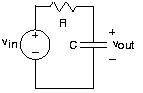
For the above example RC circuit, let
\[v_{in}=V_{in}e^{i2\pi ft} \nonumber \]
The complex amplitude Vin determines the size of the source and its phase. The critical consequence of assuming that sources have this form is that all voltages and currents in the circuit are also complex exponentials, having amplitudes governed by KVL, KCL, and the v-i relations and the same frequency as the source. To appreciate why this should be true, let's investigate how each circuit element behaves when either the voltage or current is a complex exponential. For the resistor,
\[v=Ri \nonumber \]
When
\[v=Ve^{i2\pi ft} \nonumber \]
Then
\[i=\frac{V}{R}e^{i2\pi ft} \nonumber \]
Thus, if the resistor's voltage is a complex exponential, so is the current, with an amplitude \[I=\frac{V}{R} \nonumber \] (determined by the resistor's v-i relation) and a frequency the same as the voltage. Clearly, if the current were assumed to be a complex exponential, so would the voltage. For a capacitor,
\[i=C\frac{\mathrm{d} v}{\mathrm{d} t} \nonumber \]
Letting the voltage be a complex exponential, we have:
\[i=CVi2\pi fe^{i2\pi ft} \nonumber \]
The amplitude of this complex exponential is:
\[I=CVi2\pi f \nonumber \]
Finally, for the inductor, where
\[v=L\frac{\mathrm{d} i}{\mathrm{d} t} \nonumber \]A
Assuming the current to be a complex exponential results in the voltage having the form:
\[v=LIi2\pi fe^{i2\pi ft} \nonumber \]
Its complex amplitude is given by:
\[V=LIi2\pi f \nonumber \]
The major consequence of assuming complex exponential voltage and currents is that the ratio \[Z=\frac{V}{I} \nonumber \] for each element does not depend on time, but does depend on source frequency. This quantity is known as the element's impedance.
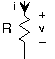
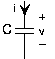
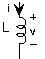
Resistor ZR=R Capacitor Zc=1/i2πfC π2π2 Inductor ZL=i2πfL
Figure 3.9.2 Impedence
The impedance is, in general, a complex-valued, frequency-dependent quantity. For example, the magnitude of the capacitor's impedance is inversely related to frequency, and has a phase of −π2-π/2. This observation means that if the current is a complex exponential and has constant amplitude, the amplitude of the voltage decreases with frequency.
Let's consider Kirchoff's circuit laws. When voltages around a loop are all complex exponentials of the same frequency, we have:
\[\sum_{nN}v_{n}=\sum_{nN}V_{n}e^{i2\pi ft}=0 \nonumber \]
which means
\[\sum_{nN}v_{n}=0 \nonumber \]
the complex amplitudes of the voltages obey KVL. We can easily imagine that the complex amplitudes of the currents obey KCL.
What we have discovered is that source(s) equaling a complex exponential of the same frequency forces all circuit variables to be complex exponentials of the same frequency. Consequently, the ratio of voltage to current for each element equals the ratio of their complex amplitudes, which depends only on the source's frequency and element values.
This situation occurs because the circuit elements are linear and time-invariant. For example, suppose we had a circuit element where the voltage equaled the square of the current:
\[v(t)=Ki^{2}(t) \nonumber \]
If
\[i(t)=Ie^{i2\pi ft}\\ v(t)=KI^{2}e^{i2\pi 2ft} \nonumber \]
meaning that voltage and current no longer had the same frequency and that their ratio was time-dependent.
Because for linear circuit elements the complex amplitude of voltage is proportional to the complex amplitude of current:
\[V=ZI \nonumber \]
assuming complex exponential sources means circuit elements behave as if they were resistors, where instead of resistance, we use impedance. Because complex amplitudes for voltage and current also obey Kirchoff's laws, we can solve circuits using voltage and current divider and the series and parallel combination rules by considering the elements to be impedances.


