6.9: Channel Models
- Page ID
- 1857
- Both wireline and wireless channels share characteristics, allowing us to use a common model for how the channel affects transmitted signals.
Both wireline and wireless channels share characteristics, allowing us to use a common model for how the channel affects transmitted signals.
- The transmitted signal is usually not filtered by the channel.
- The signal can be attenuated.
- The signal propagates through the channel at a speed equal to or less than the speed of light, which means that the channel delays the transmission.
- The channel may introduce additive interference and/or noise.
Letting α represent the attenuation introduced by the channel, the receiver's input signal is related to the transmitted one by
\[r(t)=\alpha x(t-\tau )+i(t)+n(t) \nonumber \]
This expression corresponds to the system model for the channel shown in Figure 6.9.1 below. In this book, we shall assume that the noise is white.
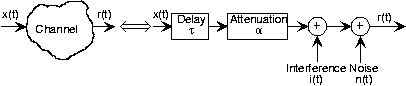
Is this model for the channel linear?
Solution
The additive-noise channel is not linear because it does not have the zero-input-zero-output property (even though we might transmit nothing, the receiver's input consists of noise).
As expected, the signal that emerges from the channel is corrupted, but does contain the transmitted signal. Communication system design begins with detailing the channel model, then developing the transmitter and receiver that best compensate for the channel's corrupting behavior. We characterize the channel's quality by the signal-to-interference ratio (SIR) and the signal-to-noise ratio (SNR). The ratios are computed according to the relative power of each within the transmitted signal's bandwidth. Assuming the signal x(t)'s spectrum spans the frequency interval [fl,fu], these ratios can be expressed in terms of power spectra.
\[SIR=\frac{2\alpha ^{2}\int_{0}^{\infty }P_{x}(f)df}{2\int_{f_{l}}^{f_{u}}P_{i}(f)df} \nonumber \]
\[SNR=\frac{2\alpha ^{2}\int_{0}^{\infty }P_{x}(f)df}{N_{0}(f_{u}-f_{l})} \nonumber \]
In most cases, the interference and noise powers do not vary for a given receiver. Variations in signal-to-interference and signal-to-noise ratios arise from the attenuation because of transmitter-to-receiver distance variations.


