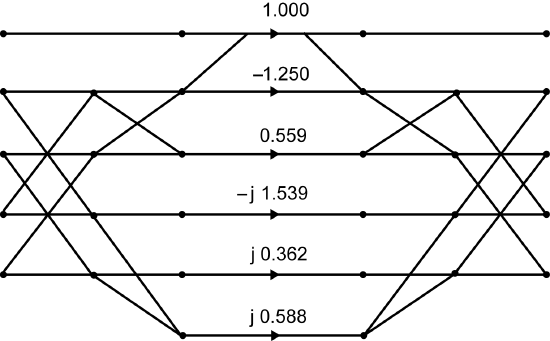
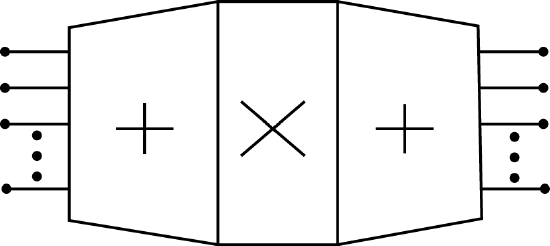
6.2: Winograd Fourier Transform Algorithm (WFTA)
- Page ID
- 1994
The operation of discrete convolution defined by
\[y(n)=\sum_{k}h(n-k)x(k) \nonumber \]
is called a bilinear operation because, for a fixed \(h(n)\), \(y(n)\) is a linear function of \(x(n)\) and for a fixed \(x(n)\) it is a linear function of \(h(n)\). The operation of cyclic convolution is the same but with all indices evaluated modulo \(N\).
Recall from Polynomial Description of Signals that length-\(N\) cyclic convolution of \(x(n)\) and \(h(n)\) can be represented by polynomial multiplication
\[Y(s)=X(s)H(s)\; mod\; (s^{N}-1) \nonumber \]
This bilinear operation can also be expressed in terms of linear matrix operators and a simpler bilinear operator denoted by \(o\) which may be only a simple element-by-element multiplication of the two vectors. This matrix formulation is
\[Y=C\left [ AX_{0}BH \right ] \nonumber \]
where \(X\), \(H\) and \(Y\) are length-\(N\) vectors with elements of \(x(n)\), \(h(n)\), and \(y(n)\) respectively. The matrices \(A\) and \(B\) have dimension \(M\times N\), and \(C\) is \[N\times M\) with \(M\geq N\).
The elements of \(A\), \(B\), and \(C\) are constrained to be simple; typically small integers or rational numbers. It will be these matrix operators that do the equivalent of the residue reduction on the polynomials in the equation.
In order to derive a useful algorithm consider the polynomial formulation equation again. To use the residue reduction scheme, the modulus is factored into relatively prime factors. Fortunately the factoring of this particular polynomial, \(s^N-1\), has been extensively studied and it has considerable structure. When factored over the rationals, which means that the only coefficients allowed are rational numbers, the factors are called cyclotomic polynomials. The most interesting property for our purposes is that most of the coefficients of cyclotomic polynomials are zero and the others are plus or minus unity for degrees up to over one hundred. This means the residue reduction will generally require no multiplications.
The operations of reducing \(X(s)\) and \(H(s)\) in the equation are carried out by the matrices \(A\) and \(B\) in the equation. The convolution of the residue polynomials is carried out by the \(o\) operator and the recombination by the CRT is done by the \(C\) matrix. The important fact is that the \(A\) and \(B\) matrices usually contain only zero and plus or minus unity entries and the \(C\) matrix only contains rational numbers. The only general multiplications are those represented by \(o\). Indeed, in the theoretical results from computational complexity theory, these real or complex multiplications are usually the only ones counted. In practical algorithms, the rational multiplications represented by \(C\) could be a limiting factor.
The \(h(n)\) terms are fixed for a digital filter, or they represent the \(W\) terms from Multidimensional Index Mapping if the convolution is being used to calculate a DFT. Because of this, \(d=BH\) in the equation can be precalculated and only the \(A\) and \(C\) operators represent the mathematics done at execution of the algorithm. In order to exploit this feature, it was shown that the properties of the equation allow the exchange of the more complicated operator \(C\) with the simpler operator \(B\). Specifically this is given by
\[Y=C\left [ AX_{0}BH \right ] \nonumber \]
\[Y'=B^{T}\left [ AX_{0}C^{T}H' \right ] \nonumber \]
where \(H'\) has the same elements as \(H\), but in a permuted order, and likewise \(Y'\) and \(Y\). This very important property allows precomputing the more complicated \(C^TH'\) in the equation rather than \(BH\) as in the above equation.
Because \(BH\) or \(C^TH'\) can be precomputed, the bilinear form of the above equations can be written as a linear form. If an \(M\times M\) diagonal matrix \(D\) is formed from \(d=C^TH'\), or in the case of the equation, \(d=BH\), assuming a commutative property for \(o\), the equations become
\[Y'=B^{T}DAX \nonumber \]
\[Y=CDAX \nonumber \]
In most cases there is no reason not to use the same reduction operations on \(X\) and \(H\), therefore, \(B\) can be the same as \(A\) and the equation then becomes
\[Y'=A^{T}DAX \nonumber \]
In order to illustrate how the residue reduction is carried out and how the \(A\) matrix is obtained, the length-\(5\) DFT algorithm started in The DFT as Convolution or Filtering will be continued. The DFT is first converted to a length-\(4\) cyclic convolution by the index permutation from The DFT as Convolution or Filtering to give the cyclic convolution in The DFT as Convolution or Filtering. To avoid confusion from the permuted order of the data \(x(n)\) in The DFT as Convolution or Filtering, the cyclic convolution will first be developed without the permutation, using the polynomial \(U(s)\)
\[U(s)=x(1)+x(3)s+x(4)s^{2}+x(2)s^{3} \nonumber \]
\[U(s)=u(0)+u(1)s+u(2)s^{2}+u(3)s^{3} \nonumber \]
and then the results will be converted back to the permuted \(x(n)\). The length-\(4\) cyclic convolution in terms of polynomials is
\[Y(s)=U(s)H(s)\; mod\; (s^{4}-1) \nonumber \]
and the modulus factors into three cyclotomic polynomials
\[s^{4}-1=(s^{2}-1)(s^{2}+1) \nonumber \]
\[s^{4}-1=(s-1)(s+1)(s^{2}+1) \nonumber \]
\[s^{4}-1=P_{1}P_{2}P_{3} \nonumber \]
Both \(U(s)\) and \(H(s)\) are reduced modulo these three polynomials. The reduction modulo \(P_1\) and \(P_2\) is done in two stages. First it is done modulo (\(s^2-1\)), then that residue is further reduced modulo (\(s-1\)) and (\(s+1\).
\[U(s)=u_{0}+u_{1}s+u_{2}s^{2}+u_{3}s^{3} \nonumber \]
\[U'(s)=((U(s)))_{(s^{2}-1)}=(u_{0}+u_{2})+(u_{1}+u_{3})s \nonumber \]
\[U1(s)=((U'(s)))_{P_{1}}=(u_{0}+u_{1}+u_{2}+u_{3}) \nonumber \]
\[U2(s)=((U'(s)))_{P_{2}}=(u_{0}-u_{1}+u_{2}-u_{3}) \nonumber \]
\[U3(s)=((U'(s)))_{P_{3}}=(u_{0}-u_{2})+(u_{1}-u_{3})s \nonumber \]
The reduction in the equation of the data polynomial equation can be denoted by a matrix operation on a vector which has the data as entries.
\[\begin{bmatrix} 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1 \end{bmatrix}\begin{bmatrix} u_{0}\\ u_{1}\\ u_{2}\\ u_{3} \end{bmatrix}=\begin{bmatrix} u_{0}+u_{2} \\ u_{1}+u_{3} \end{bmatrix} \nonumber \]
and the reduction in the equation is
\[\begin{bmatrix} 1 & 0 & -1 & 0\\ 0 & 1 & 0 & -1 \end{bmatrix}\begin{bmatrix} u_{0}\\ u_{1}\\ u_{2}\\ u_{3} \end{bmatrix}=\begin{bmatrix} u_{0}-u_{2} \\ u_{1}-u_{3} \end{bmatrix} \nonumber \]
Combining the two equations gives one operator
\[\begin{bmatrix} 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1\\ 1 & 0 & -1 & 0\\ 0 & 1 & 0 & -1 \end{bmatrix}\begin{bmatrix} u_{0}+u_{2}\\ u_{1}+u_{3}\\ u_{0}-u_{2}\\ u_{1}-u_{3} \end{bmatrix}=\begin{bmatrix} u_{0}+u_{2}\\ u_{1}+u_{3}\\ u_{0}-u_{2} \\ u_{1}-u_{3} \end{bmatrix}=\begin{bmatrix} w_{0}\\ w_{1}\\ v_{0}\\ v_{1} \end{bmatrix} \nonumber \]
Further reduction of \(v_{0}+v_{1}s\) is not possible because \(P_{3}=s^{2}+1\) cannot be factored over the rationals. However \(s^{2}-1\) can be factored into \(P_{1}P_{2}=(s-1)(s+1)\) and, therefore, \(w_{0}+w_{1}s\) can be further reduced as was done in the above equations by
\[\begin{bmatrix} 1 & 1 \end{bmatrix}\begin{bmatrix} w_{0}\\ w_{1} \end{bmatrix}=w_{0}+w_{1}=u_{0}+u_{2}+u_{1}+u_{3} \nonumber \]
Combining all the equations gives
\[\begin{bmatrix} 1 & 1 & 0 & 0\\ 1 & -1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1\\ 1 & 0 & -1 & 0\\ 0 & 1 & 0 & -1 \end{bmatrix}\begin{bmatrix} u_{0}\\ u_{1}\\ u_{2}\\ u_{3} \end{bmatrix}=\begin{bmatrix} r_{0}\\ r_{1}\\ v_{0}\\ v_{1} \end{bmatrix} \nonumber \]
The same reduction is done to \(H(s)\) and then the convolution of the equation is done by multiplying each residue polynomial of \(X(s)\) and \(H(s)\) modulo each corresponding cyclotomic factor of \(P(s)\) and finally a recombination using the polynomial Chinese Remainder Theorem (CRT) as in Polynomial Description of Signals.
\[Y(s)=K_{1}(s)U_{1}(s)H_{1}(s)+K_{2}(s)U_{2}(s)H_{2}(s)+K_{3}(s)U_{3}(s)H_{3}(s)\; mod\; (s^{4}-1) \nonumber \]
where \(U_1(s)=r_1\) and \(U_1(s)=r_1\) are constants and \(U_{3}(s)=v_{0}+v_{1}(s)\) is a first degree polynomial. \(U_1\) times \(H_1\) and \(U_2\) times \(H_2\) are easy, but multiplying \(U_3\) times \(H_3\) modulo (\(s^2+1\)) is more difficult.
The multiplication of times \(U_3(s)\) times \(H_3(s)\) can be done by the Toom-Cook algorithm which can be viewed as Lagrange interpolation or polynomial multiplication modulo a special polynomial with three arbitrary coefficients. To simplify the arithmetic, the constants are chosen to be plus and minus one and zero.
For this example it can be verified that
\[((v0+v1s)(h0+h1s))_{s^{2}+1}=(v_{0}h_{0}-v_{1}h_{1})+(v_{0}h_{1}-v_{1}h_{0})s \nonumber \]
which by the Toom-Cook algorithm or inspection is
\[\begin{bmatrix} 1 & -1 & 0\\ -1 & -1 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0\\ 0 & 1\\ 1 & 1 \end{bmatrix}\begin{bmatrix} v_{0}\\ v_{1} \end{bmatrix}o\begin{bmatrix} 1 & 0\\ 0 & 1\\ 1 & 1 \end{bmatrix}\begin{bmatrix} h_{0}\\ h_{1} \end{bmatrix}=\begin{bmatrix} y_{0}\\ y_{1} \end{bmatrix} \nonumber \]
where \(o\) signifies point-by-point multiplication. The total \(A\) matrix in is a combination of
\[AX=A_{1}A_{2}A_{3}X \nonumber \]
\[AX=\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 1 \end{bmatrix}\begin{bmatrix} 1 & 1 & 0 & 0\\ 1 & -1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1\\ 1 & 0 & -1 & 0\\ 0 & 1 & 0 & -1 \end{bmatrix}\begin{bmatrix} u_{0}\\ u_{1}\\ u_{2}\\ u_{3} \end{bmatrix}=\begin{bmatrix} r_{0}\\ r_{1}\\ v_{0}\\ v_{1} \end{bmatrix} \nonumber \]
where the matrix \(A_3\) gives the residue reduction (\(s^2-1\)) and (\(s^2+1\)) , the upper left-hand part of \(A_2\) gives the reduction modulo \(s-1\) and \(s+1\), and the lower right-hand part of \(A_1\) carries out the Toom-Cook algorithm modulo \(s^2+1\) with the multiplication in the \(Y\) equation. Notice that by calculating the equation in the three stages, seven additions are required. Also notice that \(A_1\) is not square. It is this “expansion" that causes more than \(N\) multiplications to be required in \(o\) or \(D\) in the \(Y\) equation. This staged reduction will derive the \(A\) operator.
The method described above is very straight-forward for the shorter DFT lengths. For \(Y\), both of the residue polynomials are constants and the multiplication given by \(o\) in the equation is trivial. For \(N=5\), which is the example used here, there is one first degree polynomial multiplication required but the Toom-Cook algorithm uses simple constants and, therefore, works well as indicated in the equation. For \(N=7\), there are two first degree residue polynomials which can each be multiplied by the same techniques used in the \(N=5\) example. Unfortunately, for any longer lengths, the residue polynomials have an order of three or greater which causes the Toom-Cook algorithm to require constants of plus and minus two and worse. For that reason, the Toom-Cook method is not used, and other techniques such as index mapping are used that require more than the minimum number of multiplications, but do not require an excessive number of additions. The resulting algorithms still have the structure of the equation. Blahut and Nussbaumer have a good collection of algorithms for polynomial multiplication that can be used with the techniques discussed here to construct a wide variety of DFT algorithms.
The constants in the diagonal matrix \(D\) can be found from the CRT matrix \(C\) in the equation using \(d=C^{T}H'\) for the diagonal terms in \(D\). As mentioned above, for the smaller prime lengths of \(3\), \(5\), and \(7\) this works well but for longer lengths the CRT becomes very complicated. An alternate method for finding \(D\) uses the fact that since the linear form of the equations calculates the DFT, it is possible to calculate a known DFT of a given \(x(n)\) from the definition of the DFT in Multidimensional Index Mapping and, given the \(A\) matrix in the equation, solve for \(D\) by solving a set of simultaneous equations.
A modification of this approach also works for a length which is an odd prime raised to some power: \(N=P^M\). This is a bit more complicated but has been done for lengths of \(9\), and \(25\). For longer lengths, the conventional Cooley-Tukey type- two index map algorithm seems to be more efficient. For powers of two, there is no primitive root, and therefore, no simple conversion of the DFT into convolution. It is possible to use two generators to make the conversion and there exists a set of length \(4\), \(8\), and \(16\) DFT algorithms of the form in the equation.
In Table 6.2.1 below, an operation count of several short DFT algorithms is presented. These are practical algorithms that can be used alone or in conjunction with the index mapping to give longer DFT's as shown in The Prime Factor and Winograd Fourier Transform Algorithms. Most are optimized in having either the theoretical minimum number of multiplications or the minimum number of multiplications without requiring a very large number of additions. Some allow other reasonable trade-offs between numbers of multiplications and additions. There are two lists of the number of multiplications. The first is the number of actual floating point multiplications that must be done for that length DFT. Some of these (one or two in most cases) will be by rational constants and the others will be by irrational constants. The second list is the total number of multiplications given in the diagonal matrix \(D\) in the equation. At least one of these will be unity ( the one associated with \(X(0)\)) and in some cases several will be unity (for \(N=2^M\)). The second list is important in programming the WFTA in The Prime Factor and Winograd Fourier Transform Algorithms.
| Length N | Mult Non-one | Mult Total | Adds |
| 2 | 0 | 4 | 4 |
| 3 | 4 | 6 | 12 |
| 4 | 0 | 8 | 16 |
| 5 | 10 | 12 | 34 |
| 7 | 16 | 18 | 72 |
| 8 | 4 | 16 | 52 |
| 9 | 20 | 22 | 84 |
| 11 | 40 | 42 | 168 |
| 13 | 40 | 42 | 188 |
| 16 | 20 | 36 | 148 |
| 17 | 70 | 72 | 314 |
| 19 | 76 | 78 | 372 |
| 25 | 132 | 134 | 420 |
| 32 | 68 | - | 388 |
Table 6.2.1 Number of Real Multiplications and Additions for a Length-N DFT of Complex Data
Because of the structure of the short DFTs, the number of real multiplications required for the DFT of real data is exactly half that required for complex data. The number of real additions required is slightly less than half that required for complex data because (\(N-1\)) of the additions needed when \(N\) is prime add a real to an imaginary, and that is not actually performed. When \(N=2m\), there are (\(N-2\)) of these pseudo additions.
The structure of these algorithms are in the form of