5.6: Economic Dispatch and Operations of Electric Utilities

Economic Dispatch and Operations of Electric Utilities

Electricity is a unique commodity in that it cannot generally be stored at a large scale at reasonable cost, so the entities that operate the transmission grid need to make plans and take actions to keep supply and demand matched in "real-time" - from minute to minute and second to second. Except in circumstances where regulations have prohibited such actions, the electric utility industry has historically broken the process of meeting customer demands into three stages. The sections below discuss each of the three stages under the assumption that all relevant plans and actions are undertaken by a regulated vertically-integrated electric utility.

Resource planning

Days to years in advance, utilities have acquired stores of electric generation capacity through several mechanisms including the construction of new generation plants (and supporting transmission lines), long-term forward contracting, and smaller quantities of spot-market purchases. Construction of new generation plants typically needs to happen years in advance, while forward and spot market contracts may be signed for periods varying from years in advance to a day or hour in advance. Utilities operating in states that have by and large retained the regulated and vertically-integrated structure submit resource plans to their respective state regulatory commissions through a process known as "integrated resource planning."

Generation unit commitment

Days to hours in advance, utilities make "commitment" decisions to have certain quantities of existing generation plant available to produce electricity when the need arises. In some cases (such as nuclear plants or hydroelectric facilities), the commitment decisions are made many weeks or months in advance. The decision to commit a generating unit to be able to produce electricity means that the utility is willing to incur fixed costs related to unit startup in order to have that generating plant ready and available to produce electricity in real time.

Generators with large start-up costs or long minimum-run times (such as large combustion turbines and nuclear power plants) cannot run optimally if their output is determined using a single-period analysis (a "period" in the electric power industry usually refers to a length of time of about an hour). Instead, their operation must be scheduled over a longer time horizon of days or even weeks. A utility would need a forecast of demand weeks in advance before turning on a generator with a long minimum run time. They would need to look at the demand forecast over that period of weeks and decide the lowest-cost mix of generation plants that would meet the demand. This decision is referred to as the unit-commitment decision, and it is aptly named. The utility would, weeks in advance of consumption, have to commit to using a given mix of generation resources. If demand were to deviate wildly (and unexpectedly) from the utility's forecast, it would be faced with the decision of curtailing output from some of its generators (if it over-estimated demand) or utilizing generators with fast start times but high costs (if it under-estimated demand).

Dispatch

Close to the real-time point of consumption (i.e., minutes ahead of real time), LSEs issue dispatch orders to existing generation facilities, setting specific output levels for each. LSEs also utilize some generation facilities to provide "ancillary services," which represent very fast (sub-second to minutes) automatic adjustments to keep supply and demand in balance. The process of dispatching generation plants to meet customer demands within a specified control footprint is variously known as "economic dispatch" or "optimal power flow." The terminology here is suggestive that generation plants are dispatched in such a way as to minimize the total cost of delivered electricity.

The economic dispatch algorithm actually implemented is conceptually pretty simple. Begin by turning on (or "dispatching") your generation source with the lowest "marginal" or operational costs. Have that generation source increase output until all load is met or the generation source hits its capacity constraint, whichever comes first. If the cheapest generation source hits its capacity constraint before all the demand is met, the second-cheapest generation source is turned on, and increases power until either it reaches its capacity constraint or all the demand is met. The process continues by successively turning on more expensive generation sources until the entire load is served. It is important to realize that the economic dispatch algorithm does not consider any fixed costs of power plants - only those costs directly associated with plant operation (for fossil-fired power plants, this would be primarily fuel).

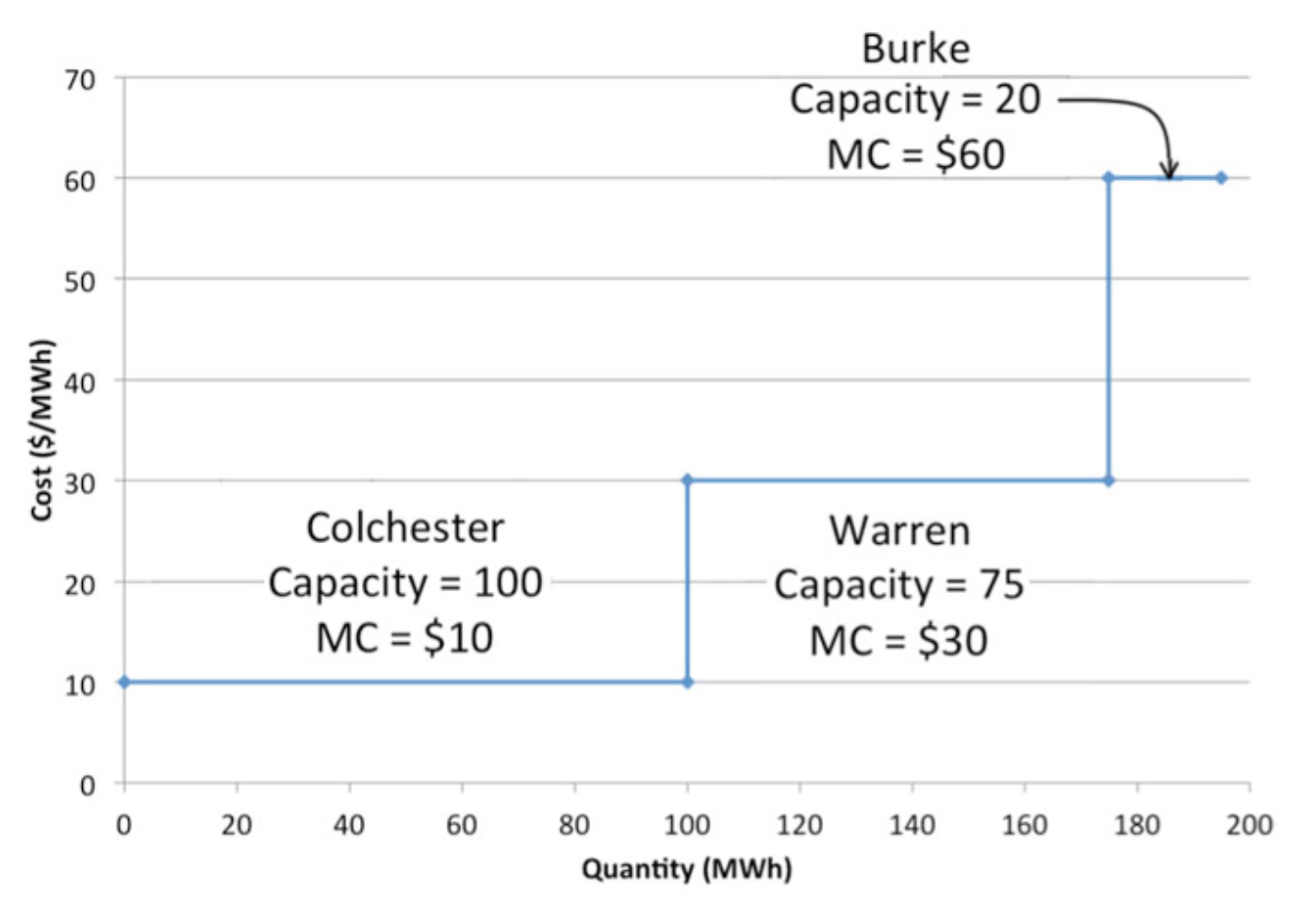
Economic dispatch is best illustrated using an example. Suppose that you were an electric utility that had three generators that could be used to meet electricity demand, as shown in \(Table \text { } 5.1\). The fixed costs would represent land leases, fuel/transmission interconnections and any other costs that do not depend on the level of output. The marginal cost measures the amount of money that it costs each plant to produce one megawatt-hour of electric energy.

\(Table \text { } 5.3\): Fleet of power plants for economic dispatch example.

Plant Name	Capacity (MW)	Fixed Costs	Marginal Cost ($/MWh)
Colchester	100	50	10
Warren	75	25	30
Burke	20	10	60

Suppose that demand during some time period was 150 MWh. The process of determining economic dispatch would follow three steps.

First, order the plants from lowest to highest marginal cost, which will tell you which plants would be utilized to produce electricity given some level of demand. This picture is called the "dispatch curve," shown in \(Figure \text { } 5.6\). Each step in the dispatch curve represents one power plant. The height of the step represents the marginal cost of electricity production for each plant. The width of each step represents the capacity of each plant. Note that the x-axis represents total capacity for the entire utility, not the capacity for any individual power plant.

\(Figure \text { } 5.6\): Dispatch curve for the three-generator example.

To determine which plants would be operating if demand was 150 MWh, you would draw a straight vertical line through the amount 150 MWh. Any capacity to the left of this line would be dispatched, while any capacity to the right of the line would not be dispatched. This is shown in \(Figure \text { } 5.7\).

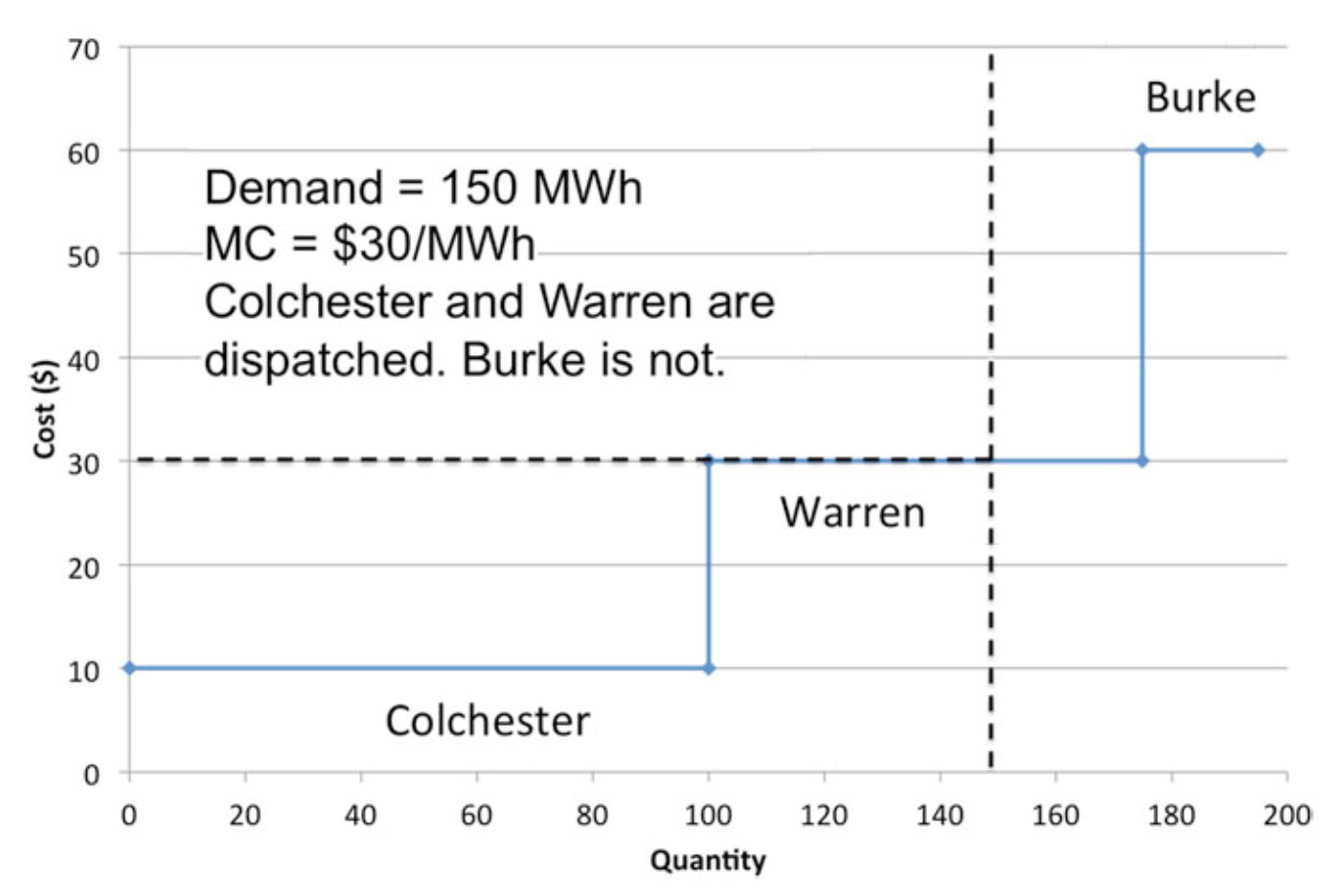
\(Figure \text { } 5.7\): Economic dispatch for the three generator example.

In this case, to meet the demand of 150 MWh, the utility would dispatch Colchester at its maximum output (100 MWh) and would meet the remaining 50 MWh of demand using the Warren plant. The Burke plant (the most expensive of the lot) is not dispatched.

We can use the dispatch information to calculate several cost measures for our hypothetical electric utility.

Total Cost is the sum of all costs incurred to meet electricity demand. To obtain total cost, we would multiply quantity produced times marginal cost for each plant, and then add in the fixed costs for all plants. Note that we need to add fixed costs even for plants that do not produce anything.

Average Cost is Total Cost divided by the total amount of electricity produced.

System Marginal Cost is the marginal cost of the generating plant that meets the last MWh of electricity demanded. The system marginal cost is also referred to as the "system lambda."

We can now calculate these cost measures for our example. The economic dispatch of all power plants in the system is:

• Colchester produces 100 MWh
• Warren produces 50 MWh
• Burke produces 0 MWh.

\(\begin{array}{l}
\text { Total cost }=(\$ 50+\$ 25+\$ 10)+\$ 10 / M W h \times 100 M W h+\$ 30 / M W h \times 50 M W h+\$ 60 / M W h \times 0 M W h=\$ 2,585 \\
\text { Average cost }=\$ 2,585 / 150 M W h=\$ 17.23 / M W h
\end{array}\)

System Lambda

The "marginal generator" (the plant used to meet the last MWh of demand) is the Warren plant. So, the system lambda would just be the marginal cost of the Warren plant, which is $30/MWh.

Note the different units for total cost ($) versus average cost and marginal cost ($/MWh).

Here is an exercise that you can try on your own. Take the same three-generator example and suppose that demand was 190 MWh. Verify that:

• Total cost = $4,235
• Average cost = $22.29/MWh
• System lambda = $60/MWh