2.2: Population Growth Models
- Page ID
- 12226
Populations change over time and space as individuals are born or immigrate (arrive from outside the population) into an area and others die or emigrate (depart from the population to another location). Populations grow and shrink and the age and gender composition also change through time and in response to changing environmental conditions. Some populations, for example trees in a mature forest, are relatively constant over time while others change rapidly. Using idealized models, population ecologists can predict how the size of a particular population will change over time under different conditions.
2.2.1: Exponential Growth
Charles Darwin, in his theory of natural selection, was greatly influenced by the English clergyman Thomas Malthus. Malthus published a book (An Essay on the Principle of Population) in 1798 stating that populations with unlimited natural resources grow very rapidly. According to the Malthus’ model, once population size exceeds available resources, population growth decreases dramatically. This accelerating pattern of increasing population size is called exponential growth, meaning that the population is increasing by a fixed percentage each year. When plotted (visualized) on a graph showing how the population size increases over time, the result is a J-shaped curve (Figure \(\PageIndex{1}\)). Each individual in the population reproduces by a certain amount (r) and as the population gets larger, there are more individuals reproducing by that same amount (the fixed percentage). In nature, exponential growth only occurs if there are no external limits.
One example of exponential growth is seen in bacteria. Bacteria are prokaryotes (organisms whose cells lack a nucleus and membrane-bound organelles) that reproduce by fission (each individual cell splits into two new cells). This process takes about an hour for many bacterial species. If 100 bacteria are placed in a large flask with an unlimited supply of nutrients (so the nutrients will not become depleted), after an hour, there is one round of division and each organism divides, resulting in 200 organisms - an increase of 100. In another hour, each of the 200 organisms divides, producing 400 - an increase of 200 organisms. After the third hour, there should be 800 bacteria in the flask - an increase of 400 organisms. After ½ a day and 12 of these cycles, the population would have increased from 100 cells to more than 24,000 cells. When the population size, N, is plotted over time, a J-shaped growth curve is produced (Figure \(\PageIndex{1}\)). This shows that the number of individuals added during each reproduction generation is accelerating – increasing at a faster rate.
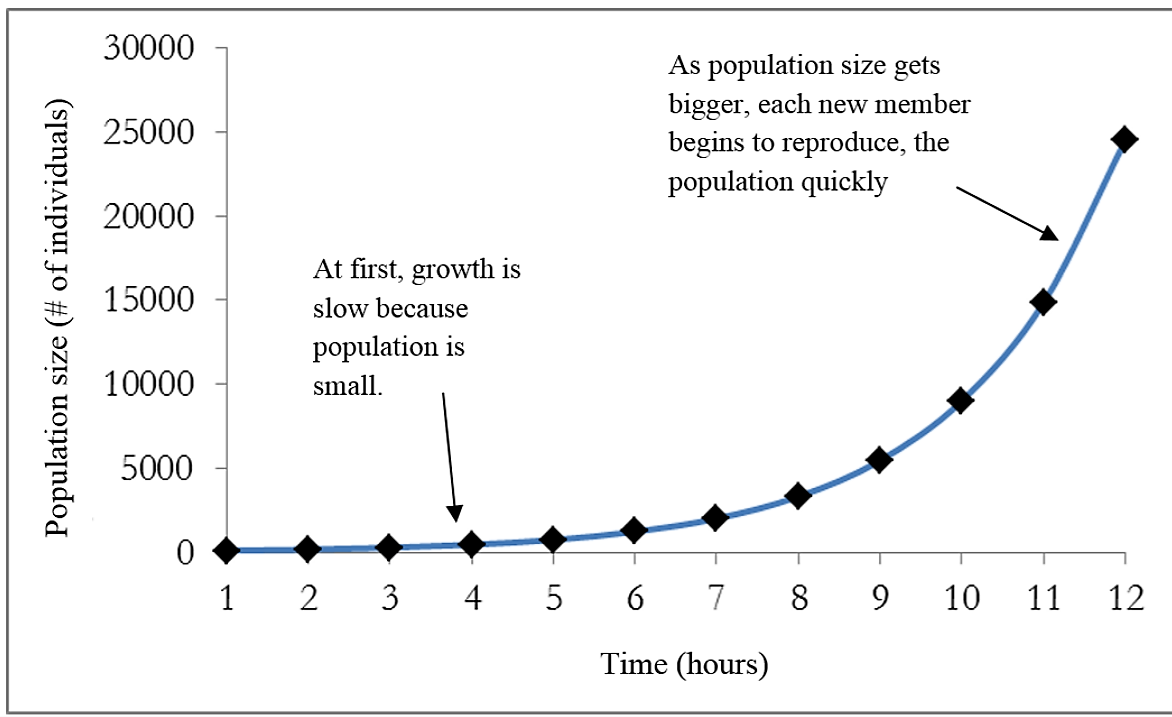.png?revision=1&size=bestfit&width=733&height=448)
This type of growth can be represented using a mathematical function known as the exponential growth model:
\[ G = r \times N \nonumber\]
also expressed as
\[ \dfrac {dN} {dt} = r \times N \nonumber\]
In these equation
- \(G\) (or \( \frac {dN} {dt} \)) is the population growth rate, it is a measure of the number of individuals added per time interval time.
- \(r\) is the per capita rate of increase (the average contribution of each member in a population to population growth; per capita means “per person”).
- \(N\) is the population size, the number of individuals in the population at a particular time.
Per capita rate of increase (r)
In exponential growth, the population growth rate (G) depends on population size (N) and the per capita rate of increase (r). In this model r does not change (fixed percentage) and change in population growth rate, G, is due to change in population size, N. As new individuals are added to the population, each of the new additions contribute to population growth at the same rate (r) as the individuals already in the population.
\[r = (\text{birth rate} + \text{immigration rate}) – (\text{death rate and emigration rate}). \nonumber\]
- If \(r\) is positive (> zero), the population is increasing in size; this means that the birth and immigration rates are greater than death and emigration.
- If \(r\) is negative (< zero), the population is decreasing in size; this means that the birth and immigration rates are less than death and emigration rates.
- If \(r\) is zero, then the population growth rate (\(G\)) is zero and population size is unchanging, a condition known as zero population growth. “\(r\)” varies depending on the type of organism, for example a population of bacteria would have a much higher “r” than an elephant population. In the exponential growth model \(r\) is multiplied by the population size, \(N\), so population growth rate is largely influenced by \(N\). This means that if two populations have the same per capita rate of increase (\(r\)), the population with a larger N will have a larger population growth rate than the one with a smaller \(N\).
2.2.2: Logistic Growth
Exponential growth cannot continue forever because resources (food, water, shelter) will become limited. Exponential growth may occur in environments where there are few individuals and plentiful resources, but soon or later, the population gets large enough that individuals run out of vital resources such as food or living space, slowing the growth rate. When resources are limited, populations exhibit logistic growth. In logistic growth a population grows nearly exponentially at first when the population is small and resources are plentiful but growth rate slows down as the population size nears limit of the environment and resources begin to be in short supply and finally stabilizes (zero population growth rate) at the maximum population size that can be supported by the environment (carrying capacity). This results in a characteristic S-shaped growth curve (Figure \(\PageIndex{2}\)). The mathematical function or logistic growth model is represented by the following equation:
\[ G= r \times N \times \left(1 - \dfrac {N}{K}\right) \nonumber\]
where \(K\ ) is the carrying capacity – the maximum population size that a particular environment can sustain (“carry”). Notice that this model is similar to the exponential growth model except for the addition of the carrying capacity. In the exponential growth model, population growth rate was mainly dependent on N so that each new individual added to the population contributed equally to its growth as those individuals previously in the population because per capita rate of increase is fixed. In the logistic growth model, individuals’ contribution to population growth rate depends on the amount of resources available (K). As the number of individuals (N) in a population increases, fewer resources are available to each individual. As resources diminish, each individual on average, produces fewer offspring than when resources are plentiful, causing the birth rate of the population to decrease.
.png?revision=1&size=bestfit&width=703&height=422)
Influence of K on population growth rate
In the logistic growth model, the exponential growth \( (r \times N) \) is multiplied by fraction or expression that describes the effect that limiting factors \( ( 1- \frac {N} {K})\) have on an increasing population. Initially when the population is very small compared to the capacity of the environment (K), \( 1- \frac {N} {K}\) is a large fraction that nearly equals 1 so population growth rate is close to the exponential growth \( (r \times N) \). For example, supposing an environment can support a maximum of 100 individuals and N = 2, N is so small that \( 1- \frac {N} {K}\) \( 1- \frac {2}{100} = 0.98 \) will be large, close to 1. As the population increases and population size gets closer to carrying capacity (N nearly equals K), then \(1- \frac {N} {K}\)is a small fraction that nearly equals zero and when this fraction is multiplied by \(r \times N\), population growth rate is slowed down. In the earlier example, if the population grows to 98 individuals, which is close to (but not equal) K, then \( 1- \frac {N} {K} \: (1 - \frac {98} {100} = 0.02) \) will be so small, close to zero. If population size equals the carrying capacity, \( \frac {N}{K} = 1\), so \( 1- \frac {N}[K} = 0 \), population growth rate will be zero (in the above example, \( 1- \frac {100}{100} = 0\). This model, therefore, predicts that a population’s growth rate will be small when the population size is either small or large, and highest when the population is at an intermediate level relative to K. At small populations, growth rate is limited by the small amount of individuals (N) available to reproduce and contribute to population growth rate whereas at large populations, growth rate is limited by the limited amount of resources available to each of the large number of individuals to enable them reproduce successfully. In fact, maximum population growth rate (G) occurs when N is half of K.
.png?revision=1&size=bestfit&width=748&height=374)
Yeast is a microscopic fungus, used to make bread and alcoholic beverages, that exhibits the classical S-shaped logistic growth curve when grown in a test tube (Figure \(\PageIndex{3}\)). Its growth levels off as the population depletes the nutrients that are necessary for its growth. In the real world, however, there are variations to this idealized curve. For example, a population of harbor seals may exceed the carrying capacity for a short time and then fall below the carrying capacity for a brief time period and as more resources become available, the population grows again (Figure \(\PageIndex{4}\)). This fluctuation in population size continues to occur as the population oscillates around its carrying capacity. Still, even with this oscillation, the logistic model is exhibited.
.png?revision=1&size=bestfit&width=817&height=394)

