7.5: Insulation and Home Heating Fuels (I)

R-Value

As you may recall from the first part of this lesson, R-value is a wall's capacity to resist heat loss or its thermal resistance. Insulation materials are rated in terms of their R-value, with a higher R-value indicating better insulating effectiveness.

The R-value of thermal insulation depends on the type of material, its thickness, and its density. Generally, walls are not made up of just one material or one layer.

R-values for most commonly used building materials are given in the table below. From looking at Table 7.5.1, we can see that natural materials like stone and bricks are not good insulation materials, but most of the synthetic insulation products such as polystyrene or polyurethane are very effective insulation materials.

Table 7.5.1. Building materials and their R-values

Material	R-Value (ft^2 o Fh / BTU)
Plain glass (1/8 inch)	0.03
Stone (1 inch)	0.08
Common brick (1 inch)	0.20
Asphalt roof shingles	0.44
Gypsum board, drywall or plasterboard (1/2 inch)	0.45
Wood siding (1/2 inch)	0.81
Plywood (3/4 inch)	0.94
Insulating sheathing (3/4 inch)	2.06
Fiberglass, battens (1 inch)	3.50
Polystyrene (1 inch)	5.00
Polyurethane board	6.25

If insulation materials have a low R-value per inch, then they will need to be thicker than those materials with a higher R-value per inch to achieve the same degree of effectiveness in resisting heat loss.

Figure 7.5.1 compares the thickness required of various insulation materials to achieve the same R-Value of 22.

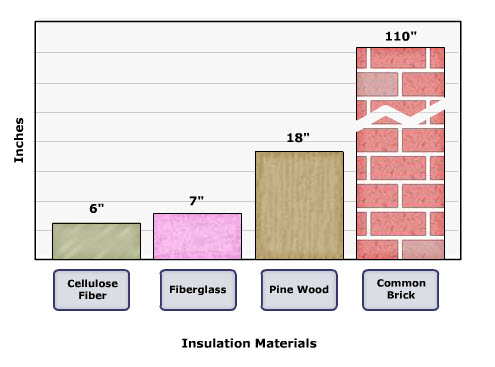
Figure 7.5.1. Thicknesses to attain R-value of 22

Types of Insulation

Refer to Table 7.5.2 to learn about various types of insulation.

Table 7.5.2. Types of insulation

Insulation	What is it made of?	What does it look like?	Additional Information
Fiberglass	Molten glass spun into microfibers	Pink or yellow in the form of batts or rolled blankets
Rock wool	Rock	Gray or brown fibers in batts or blankets, or shredded loose fill	Manufactured in a similar way as fiberglass, but with molten rock instead of glass
Cellulose	Recycled paper - newspaper or cardboard shredded into small bits of fiber	Blown in as loose fill	Treated with fire- and insect-resistant chemicals
Rigid foam	Different types, but some are made from post-consumer recycled content from fast food containers and cups	Rigid sheets that are applied directly to framing	Best where space is limited, but a high R-value is needed. Can be installed on the interior of a wall, but if installed inside, must be covered by fire-resistant material like woodboard. One drawback to foam is that it deteriorates unless it is protected from prolonged exposure to sunlight and water. It is also more expensive than other insulation.
Synthetic insulation	Usually polystyrene or polyurethane foam	Polystyrene: rigid boards Polyurethane: rigid boards or sprayed in space systems	Polystyrene is used for insulating basements, cathedral ceilings, or sidewalls. Polyurethane foams are high-performance insulating materials.

Composite Wall R-Values

Generally, walls are made up of several layers of different materials. The R-value of a composite wall is calculated by adding the effective R-values of each of the layers of the wall.

For example, Figure 7.5.2 shows a wall made up of four layers — ½ inch drywall inside for aesthetic purposes, real insulation in between the studs, ¾ inch plywood sheathing outside, and wood siding as the final exterior finish. Together, the layers of the wall are preventing heat loss.

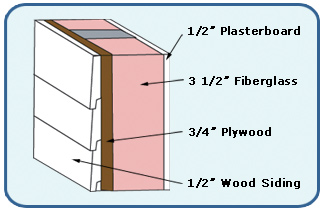
Figure 7.5.2. Diagram of a wall

We can calculate this wall’s composite R-value by adding the R-values of each layer.

Plasterboard (1/2 inch)
+ Fiberglass (3.5 inches @ 3.70 per inch)
+ Plywood (3/4 inches)
+ Wood Siding (1/2 inch)
-----------------------------------------
Total R-Value of Composite Wall

We can find the R-values for the walls by using Table 7.2.1 from the R-values section.

Thus,

Plasterboard (1/2 inch) = 0.4524
+ Fiberglass (3.5 inches @ 3.70 per inch) = 12.95
+ Plywood (3/4 inches) = 0.94
+ Wood Siding (1/2 inch) = 0.81
-----------------------------------------
Total R-Value of Composite Wall = 15.15 \( \dfrac{ft^2 °F h}{Btu} \)

Example Problems

Example 1

A ceiling is insulated with 0.75" plywood, 2" of polystyrene board, and a 3" layer of fiberglass. What is the R-value for the ceiling?

Answer

The ceiling consists of three layers, and all three layers together prevent the heat loss. So, we need to add the R-values of all three layers

3/4" in plywood has an R-value of 0.94
2" of polystyrene at 5.0 per inch will have an R-value of 10.00
3" of fiberglass at 3.7 per inch will have an R-value of 11.10

So the R-value of the ceiling is \( \dfrac{ft^2 °F h}{Btu} \).

Example 2

A wall consists of 0.5” wood siding (R = 0.81), 0.75” plywood (R = 0.94), 3.5” of fiberglass (R = 13.0), and 0.5” plasterboard (R = 0.45). What is the composite R-value of the wall?

Answer

The following video provides the solution.

Example 3

What is the R-value of a wall that is made up of wood siding (R = 0.81), 5” of fiberglass (R = 3.70 per inch), and a layer of 0.5” drywall (R = 0.45)?

Answer

The following video covers the solution.

Example 4

A wall is made up of 8” of stone, 3” of polyurethane board, and 0.75” of plywood. Calculate the composite R-value for the wall.

Answer

The following video covers the solution.