9.1: Constructing Block Diagrams- Visualizing control measurements
- Page ID
- 22614
It is often convenient to express a control system with a block diagram. These diagrams help to visualize the relationships between each part of the control system (Figure \(\PageIndex{1}\)).
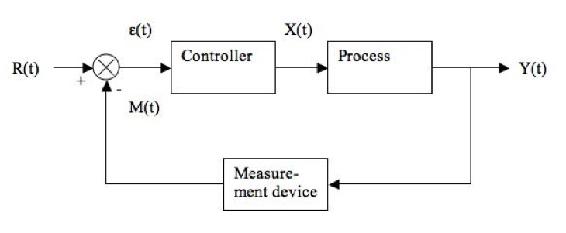
The control system shown is called a closed-loop system or a feedback system because the measured value of the controlled variable is returned or "fed back" to the comparator. In the comparator the controlled variable is compared with the desired value or set point. If there is any difference between the measured variable and the set point, an error is generated. This error enters a controller, which in turns adjusts the final control element to return the controlled variable to the set point [1].
- R(t) = "set point", is a synonym for the desired value of the controlled variable
- ε(t) = process error or comparator
- X(t) = process variable
- M(t) = measurement variable
- Y(t) = output variable
The "hat" above the G indicates that it is an operator (not a simple function) and may include integration and differentiation. Thus, you cannot divide by a 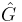 , but have to multiply both sides by its inverse
, but have to multiply both sides by its inverse 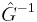 (see below). This is a more general representation that the standard Laplace transform form; here it is not necessary that the operators be linear.
(see below). This is a more general representation that the standard Laplace transform form; here it is not necessary that the operators be linear.
From the block diagram the equations for a system can be constructed. Define the following:
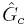 =Controller operator
=Controller operator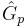 =Process operator
=Process operator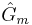 =Measurement delay operator
=Measurement delay operator
The equations for the system in Figure \(\PageIndex{1}\) are given below. Note that these equations are always written as "output is equal to operator applied to input."
- Process:
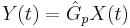
- Controller:
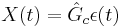
- Comparator: ε(t) = R(t) − M(t)
- Measurement delay:
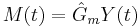
Typically to plot the response of the controller, \(Y(t)\), it is necessary to solve these equations to obtain a single equation for \(Y(t)\). This can be done by first plugging the measurement delay equation into the compartor equation, or.
\[\epsilon(t)=R(t)-\hat{G}_{m} Y(t).\nonumber \]
This equation can be put into the controller equation, or
\[X(t)=\hat{G}_{c}\left[R(t)-G_{m} Y(t)\right].\nonumber \]
Finally, the equation for \(Y(t)\) can be obtained by putting the above equation into the equation for the process, or
\[Y(t)=\hat{G}_{p} \hat{G}_{c}\left[R(t)-\hat{G}_{m} Y(t)\right].\nonumber \]
Frequently we have a differential equation for \(X(t)\) in terms of derivatives of \(Y(t)\) so we write
\[X(t)=\hat{G}_{p}^{-1} Y(t)\nonumber \]
which implies the form of the general equation
\[\hat{G}_{p}^{-1} Y(t)=\hat{G}_{c}\left[R(t)-G_{m} Y(t)\right]\nonumber \]
If the process, controller, and measurement delay operators are known, \(Y(t)\) can be plotted and the response of the system can be observed (i.e. using Mathematica).
That is, we have
- \(Y(t)=\hat{G}_{p} X(t)\)
- \(X(t)=\hat{G}_{c} \epsilon(t)]\)
- \(\epsilon(t)=R(t)-M(t)\)
- \(M(t)=\hat{G}_{m} Y(t)\)
- \(\hat{G}_{p}^{-1} Y(t)=\hat{G}_{c}\left[R(t)-G_{m} Y(t)\right]\)
Assume no measurement lag:
\[\hat{G}_{m}=1\nonumber \]
Assume first-order system:
\[\hat{G}_{p}^{-1}=\frac{1}{K_{p}}\left(\tau_{p} \frac{d}{d t}+1\right)\nonumber \]
Assume PI controller:
\[\hat{G}_{c}^{-1}=K_{c}+\frac{K_{c}}{\tau_{I}} \int_{0}^{t} d t\nonumber \]
Substituting equations (2) and (3) into (5) gives:
\[\frac{1}{K_{p}}\left(\tau_{p} \frac{d}{d t} \quad 1\right) Y(t)=\left(K_{z}, \frac{K_{e}}{_{\eta_{1}}} \int_{0}^{t} a t\right) c(t)-\left(K_{z} | \frac{K_{c}}{_{7_{1}}} \int_{0}^{t} d t\right)\{H(t) \quad Y(t)\nonumber \]
Simplifying further gives:
\[\tau_{p} Y^{\prime}(t)+Y(t)=K_{c}(R(t)-Y(t))+\frac{K_{c}}{\tau_{I}}(R(t)-Y(t))\nonumber \]
Differentiating the above equation gives:
\[\tau_{p} Y^{\prime \prime}(t)+Y^{\prime}(t)=K_{c} R^{\prime}(t)-K_{c} Y^{\prime}(t)+\frac{K_{c}}{\tau_{I}} R(t)-\frac{K_{c}}{\tau_{I}} Y(t)\nonumber \]
Rearranging the above equation:
\[\tau_{p} Y^{\prime \prime}(t)+\left(1+K_{c}\right) Y^{\prime}(t)+\frac{K_{c}}{\tau_{I}} Y(t)=K_{c} R^{\prime}(t)+\frac{K_{c}}{\tau_{I}} R(t)\nonumber \]
Multiply the above equation by 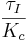 to eliminate the co-efficient of \(Y'(t)\) gives:
to eliminate the co-efficient of \(Y'(t)\) gives:
\[\frac{\tau_{I} \tau_{p}}{K_{c}} Y^{\prime \prime}(t)+\tau_{I} \frac{1+K_{c}}{K_{c}} Y^{\prime}(t)+Y(t)=\tau_{I} R^{\prime}(t)+R(t)\nonumber \]
References
- Coughanowr, D.R. and S.E. LeBlanc (2009). Process Systems Analysis And Control. Third Edition. Mc-Graw Hill.


