14.1: Design of Experiments via Taguchi Methods - Orthogonal Arrays
- Page ID
- 22674
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Taguchi method involves reducing the variation in a process through robust design of experiments. The overall objective of the method is to produce high quality product at low cost to the manufacturer. The Taguchi method was developed by Dr. Genichi Taguchi of Japan who maintained that variation. Taguchi developed a method for designing experiments to investigate how different parameters affect the mean and variance of a process performance characteristic that defines how well the process is functioning. The experimental design proposed by Taguchi involves using orthogonal arrays to organize the parameters affecting the process and the levels at which they should be varies. Instead of having to test all possible combinations like the factorial design, the Taguchi method tests pairs of combinations. This allows for the collection of the necessary data to determine which factors most affect product quality with a minimum amount of experimentation, thus saving time and resources. The Taguchi method is best used when there is an intermediate number of variables (3 to 50), few interactions between variables, and when only a few variables contribute significantly.
The Taguchi arrays can be derived or looked up. Small arrays can be drawn out manually; large arrays can be derived from deterministic algorithms. Generally, arrays can be found online. The arrays are selected by the number of parameters (variables) and the number of levels (states). This is further explained later in this article. Analysis of variance on the collected data from the Taguchi design of experiments can be used to select new parameter values to optimize the performance characteristic. The data from the arrays can be analyzed by plotting the data and performing a visual analysis, ANOVA, bin yield and Fisher's exact test, or Chi-squared test to test significance.
In this article, the specific steps involved in the application of the Taguchi method will be described and examples of using the Taguchi method to design experiments will be given.
Summary of Taguchi Method
Philosophy of the Taguchi Method
- Quality should be designed into a product, not inspected into it. Quality is designed into a process through system design, parameter design, and tolerance design. Parameter design, which will be the focus of this article, is performed by determining what process parameters most affect the product and then designing them to give a specified target quality of product. Quality "inspected into" a product means that the product is produced at random quality levels and those too far from the mean are simply thrown out.
- Quality is best achieved by minimizing the deviation from a target. The product should be designed so that it is immune to uncontrollable environmental factors. In other words, the signal (product quality) to noise (uncontrollable factors) ratio should be high.
- The cost of quality should be measured as a function of deviation from the standard and the losses should be measured system wide. This is the concept of the loss function, or the overall loss incurred upon the customer and society from a product of poor quality. Because the producer is also a member of society and because customer dissatisfaction will discourage future patronage, this cost to customer and society will come back to the producer.
Taguchi Method Design of Experiments
The general steps involved in the Taguchi Method are as follows:
- Define the process objective, or more specifically, a target value for a performance measure of the process. This may be a flow rate, temperature, etc. The target of a process may also be a minimum or maximum; for example, the goal may be to maximize the output flow rate. The deviation in the performance characteristic from the target value is used to define the loss function for the process.
- Determine the design parameters affecting the process. Parameters are variables within the process that affect the performance measure such as temperatures, pressures, etc. that can be easily controlled. The number of levels that the parameters should be varied at must be specified. For example, a temperature might be varied to a low and high value of 40 C and 80 C. Increasing the number of levels to vary a parameter at increases the number of experiments to be conducted.
- Create orthogonal arrays for the parameter design indicating the number of and conditions for each experiment. The selection of orthogonal arrays is based on the number of parameters and the levels of variation for each parameter, and will be expounded below.
- Conduct the experiments indicated in the completed array to collect data on the effect on the performance measure.
- Complete data analysis to determine the effect of the different parameters on the performance measure.
See below for a pictorial depiction of these and additional possible steps, depending on the complexity of the analysis.
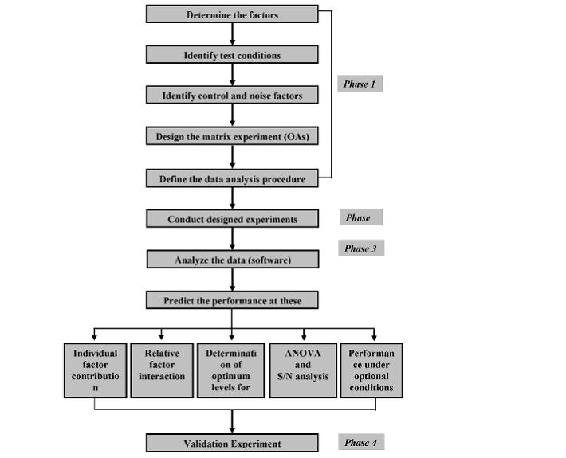
A detailed description of the execution of these steps will be discussed next.
Taguchi Loss Function
The goal of the Taguchi method is to reduce costs to the manufacturer and to society from variability in manufacturing processes. Taguchi defines the difference between the target value of the performance characteristic of a process, τ, and the measured value, y, as a loss function as shown below.
\[l(y)=k_{c}(y-\tau)^{2} \nonumber \]
The constant, kc, in the loss function can be determined by considering the specification limits or the acceptable interval, delta.
\[k_{c}=\frac{C}{\Delta^{2}} \nonumber \]
The difficulty in determining kc is that τ and C are sometimes difficult to define.
If the goal is for the performance characteristic value to be minimized, the loss function is defined as follows:
\[l(y)=k_{c} y^{2} \nonumber \]
where \(\tau=0\).
If the goal is for the performance characteristic value to maximized, the loss function is defined as follows:
\[l(y)=\frac{k_{c}}{y^{2}} \nonumber \]
The loss functions described here are the loss to a customer from one product. By computing these loss functions, the overall loss to society can also be calculated.
Determining Parameter Design Orthogonal Array
The effect of many different parameters on the performance characteristic in a condensed set of experiments can be examined by using the orthogonal array experimental design proposed by Taguchi. Once the parameters affecting a process that can be controlled have been determined, the levels at which these parameters should be varied must be determined. Determining what levels of a variable to test requires an in-depth understanding of the process, including the minimum, maximum, and current value of the parameter. If the difference between the minimum and maximum value of a parameter is large, the values being tested can be further apart or more values can be tested. If the range of a parameter is small, then less values can be tested or the values tested can be closer together. For example, if the temperature of a reactor jacket can be varied between 20 and 80 degrees C and it is known that the current operating jacket temperature is 50 degrees C, three levels might be chosen at 20, 50, and 80 degrees C. Also, the cost of conducting experiments must be considered when determining the number of levels of a parameter to include in the experimental design. In the previous example of jacket temperature, it would be cost prohibitive to do 60 levels at 1 degree intervals. Typically, the number of levels for all parameters in the experimental design is chosen to be the same to aid in the selection of the proper orthogonal array.
Knowing the number of parameters and the number of levels, the proper orthogonal array can be selected. Using the array selector table shown below, the name of the appropriate array can be found by looking at the column and row corresponding to the number of parameters and number of levels. Once the name has been determined (the subscript represents the number of experiments that must be completed), the predefined array can be looked up. Links are provided to many of the predefined arrays given in the array selector table. These arrays were created using an algorithm Taguchi developed, and allows for each variable and setting to be tested equally. For example, if we have three parameters (voltage, temperature, pressure) and two levels (high, low), it can be seen the proper array is L4. Clicking on the link L4 to view the L4 array, it can be seen four different experiments are given in the array. The levels designated as 1, 2, 3 etc. should be replaced in the array with the actual level values to be varied and P1, P2, P3 should be replaced with the actual parameters (i.e. voltage, temperature, etc.)
Array Selector

Links to Orthogonal Arrays
The following links are connected to images of the orthogonal array named in the link title:
L4 Array
L8 Array
L9 Array
L12 Array
L16 Array
L'16 Array
L18 Array
L25 Array
L27 Array
L32 Array
L'32 Array
L36 Array
L50 Array
Important Notes Regarding Selection + Use of Orthogonal Arrays
Note 1
The array selector assumes that each parameter has the same number of levels. Sometimes this is not the case. Generally, the highest value will be taken or the difference will be split.
The following examples offer insight on choosing and properly using an orthogonal array. Examples 1 and 2 focus on array choice, while Example 3 will demonstrate how to use an orthogonal array in one of these situations.
Example 1:
# parameter: A, B, C, D = 4 # levels: 3, 3, 3, 2 = ~3 array: L9
Example 2:
# parameter: A, B, C, D, E, F = 6 # levels: 4, 5, 3, 2, 2, 2 = ~3 array: modified L16
Example 3:
A reactor's behavior is dependent upon impeller model, mixer speed, the control algorithm employed, and the cooling water valve type. The possible values for each are as follows:
Impeller model: A, B, or C
Mixer speed: 300, 350, or 400 RPM
Control algorithm: PID, PI, or P
Valve type: butterfly or globe
There are 4 parameters, and each one has 3 levels with the exception of valve type. The highest number of levels is 3, so we will use a value of 3 when choosing our orthogonal array.
Using the array selector above, we find that the appropriate orthogonal array is L9:
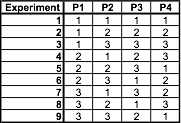
When we replace P1, P2, P3, and P4 with our parameters and begin filling in the parameter values, we find that the L9 array includes 3 levels for valve type, while our system only has 2. The appropriate strategy is to fill in the entries for P4=3 with 1 or 2 in a random, balanced way. For example:
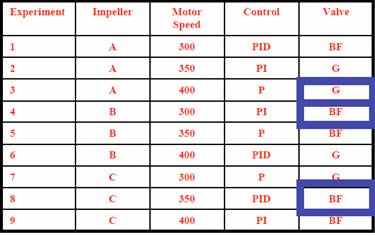
Here, the third value was chosen twice as butterfly and once as global.
Note 2
If the array selected based on the number of parameters and levels includes more parameters than are used in the experimental design, ignore the additional parameter columns. For example, if a process has 8 parameters with 2 levels each, the L12 array should be selected according to the array selector. As can be seen below, the L12 Array has columns for 11 parameters (P1-P11). The right 3 columns should be ignored.
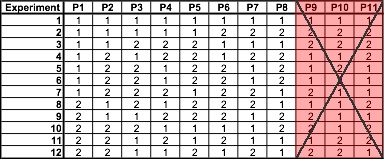
Analyzing Experimental Data
Once the experimental design has been determined and the trials have been carried out, the measured performance characteristic from each trial can be used to analyze the relative effect of the different parameters. To demonstrate the data analysis procedure, the following L9 array will be used, but the principles can be transferred to any type of array.
In this array, it can be seen that any number of repeated observations (trials) may be used. Ti,j represents the different trials with i = experiment number and j = trial number. It should be noted that the Taguchi method allows for the use of a noise matrix including external factors affecting the process outcome rather than repeated trials, but this is outside of the scope of this article.
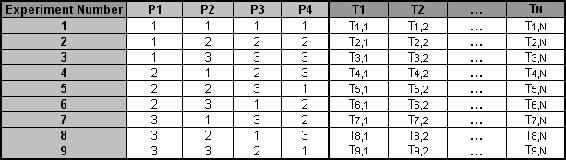
To determine the effect each variable has on the output, the signal-to-noise ratio, or the SN number, needs to be calculated for each experiment conducted. The calculation of the SN for the first experiment in the array above is shown below for the case of a specific target value of the performance characteristic. In the equations below, yi is the mean value and si is the variance. yi is the value of the performance characteristic for a given experiment.
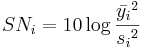
\[S N_{i}=10 \log \frac{\bar{y}_{i}^{2}}{s_{i}^{2}} \nonumber \]
where
\[\bar{y}_{i}=\frac{1}{N_{i}} \sum_{u=1}^{N_{i}} y_{i, u} \nonumber \]
\[s_{i}^{2}=\frac{1}{N_{i}-1} \sum_{u=1}^{N_{i}}\left(y_{i, u}-\bar{y}_{i}\right) \nonumber \]
and
- \(i\) is the experimental number,
- \(u\) is the trial number, and
- \(N_i\) is the numb er of trials for experiment \(i\)
For the case of minimizing the performance characteristic, the following definition of the SN ratio should be calculated:
\[S N_{i}=-10 \log \left(\sum_{u=1}^{N_{i}} \frac{y_{u}^{2}}{N_{i}}\right) \nonumber \]
For the case of maximizing the performance characteristic, the following definition of the SN ratio should be calculated:
\[S N_{i}=-10 \log \left[\frac{1}{N_{i}} \sum_{u=1}^{N_{i}} \frac{1}{y_{u}^{2}}\right] \nonumber \]
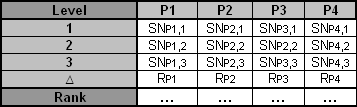
After calculating the SN ratio for each experiment, the average SN value is calculated for each factor and level. This is done as shown below for Parameter 3 (P3) in the array:
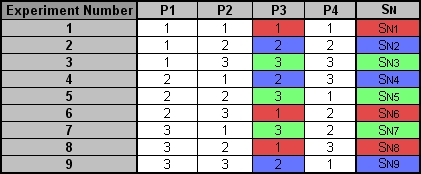
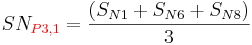
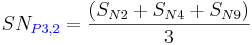
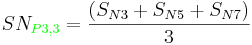
Once these SN ratio values are calculated for each factor and level, they are tabulated as shown below and the range R (R = high SN - low SN)of the SN for each parameter is calculated and entered into the table. The larger the R value for a parameter, the larger the effect the variable has on the process. This is because the same change in signal causes a larger effect on the output variable being measured.
Please refer to the Worked Out Example for a numeric example of how the data analysis procedure described here is applied.
Advantages and Disadvantages
An advantage of the Taguchi method is that it emphasizes a mean performance characteristic value close to the target value rather than a value within certain specification limits, thus improving the product quality. Additionally, Taguchi's method for experimental design is straightforward and easy to apply to many engineering situations, making it a powerful yet simple tool. It can be used to quickly narrow down the scope of a research project or to identify problems in a manufacturing process from data already in existence. Also, the Taguchi method allows for the analysis of many different parameters without a prohibitively high amount of experimentation. For example, a process with 8 variables, each with 3 states, would require 6561 (38) experiments to test all variables. However using Taguchi's orthogonal arrays, only 18 experiments are necessary, or less than .3% of the original number of experiments. In this way, it allows for the identification of key parameters that have the most effect on the performance characteristic value so that further experimentation on these parameters can be performed and the parameters that have little effect can be ignored.
The main disadvantage of the Taguchi method is that the results obtained are only relative and do not exactly indicate what parameter has the highest effect on the performance characteristic value. Also, since orthogonal arrays do not test all variable combinations, this method should not be used with all relationships between all variables are needed. The Taguchi method has been criticized in the literature for difficulty in accounting for interactions between parameters. Another limitation is that the Taguchi methods are offline, and therefore inappropriate for a dynamically changing process such as a simulation study. Furthermore, since Taguchi methods deal with designing quality in rather than correcting for poor quality, they are applied most effectively at early stages of process development. After design variables are specified, use of experimental design may be less cost effective.
Other Methods of Experimental Design
Two other methods for determining experimental design are factorial design and random design. For scenarios with a small number of parameters and levels (1-3) and where each variable contributes significantly, factorial design can work well to determine the specific interactions between variables. However, factorial design gets increasingly complex with an increase in the number of variables. For large systems with many variables (50+) where there are few interactions between variables, random design can be used. Random design assigns each variable a state based on a uniform sample (ex: 3 states = 0.33 probability) for the selected number of experiments. When used properly (in a large system), random design usually produces an experimental design that is desired. However, random design works poorly for systems with a small number of variables.
To obtain a even better understanding of these three different methods, it's good to get a visual of these three methods. It will illustrate the degree of efficiency for each experimental design depending on the number of variables and the number of states for each variable. The following will have the three experimental designs for the same scenario.
Scenario. You have a CSTR that has four(4) variables and each variable has three or two states. You are to design an experiment to systematically test the effect of each of the variables in the current CSTR.
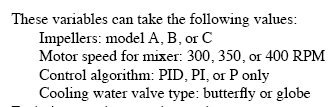
Experimental Design #1: Factorial Design By looking at the # variables and # states, there should be a total of 54 experiments because (3impellers)(3speeds)(3controllers)(2valves)=54. Here's a list of these 54 experiments:

Experimental Design #2: Taguchi Method Since you know the # of states and variables, you can refer to the table above in this wiki and obtain the correct Taguchi array. It turns out to be a L9 array.
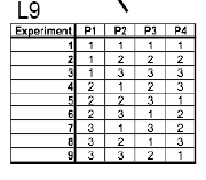
With the actual variables and states, the L9 array should look like the following:
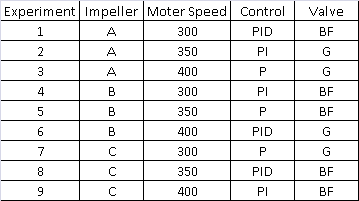
Experimental Design #3: Random Design
Since we do not know the number of signal recoveries we want and we don't know the probabilities of each state to happen, it will be difficult to construct a random design table. It will mostly be used for extreme large experiments. Refer to the link below to help you obtain a better grasp on the random design concept.
http://groups.csail.mit.edu/drl/journal_club/papers/CS2-Candes-Romberg-05.pdf
A microprocessor company is having difficulty with its current yields. Silicon processors are made on a large die, cut into pieces, and each one is tested to match specifications. The company has requested that you run experiments to increase processor yield. The factors that affect processor yields are temperature, pressure, doping amount, and deposition rate.
Determine the Taguchi experimental design orthogonal array. The operating conditions for each parameter and level are listed below:
- A: Temperature
- A1 = 100ºC
- A2 = 150ºC (current)
- A3 = 200ºC
- B: Pressure
- B1 = 2 psi
- B2 = 5 psi (current)
- B3 = 8 psi
- C: Doping Amount
- C1 = 4%
- C2 = 6% (current)
- C3 = 8%
- D: Deposition Rate
- D1 = 0.1 mg/s
- D2 = 0.2 mg/s (current)
- D3 = 0.3 mg/s
Conducting three trials for each experiment, the data below was collected. Compute the SN ratio for each experiment for the target value case, create a response chart, and determine the parameters that have the highest and lowest effect on the processor yield.
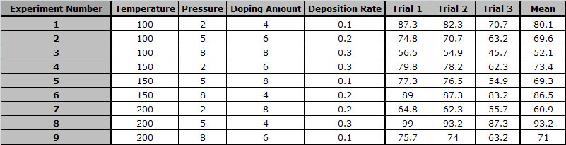
Solution
a
The L9 orthogonal array should be used. The filled in orthogonal array should look like this:
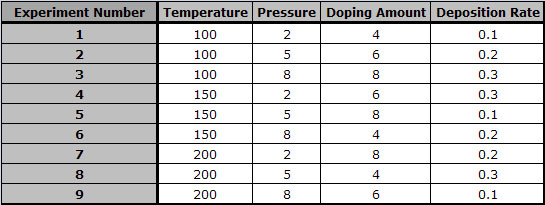
This setup allows the testing of all four variables without having to run 81 [=34=(3 Temperatures)(3 Pressures)(3 Doping Amounts)(3 Deposition rates)] separate trials.b) Question:
b) Shown below is the calculation and tabulation of the SN ratio.
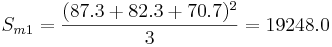
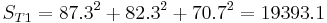
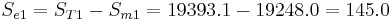
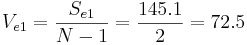
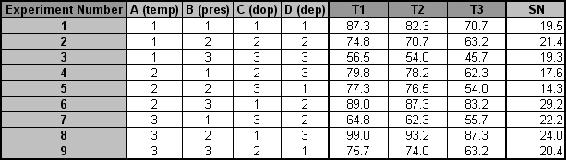
Shown below is the response table. This table was created by calculating an average SN value for each factor. A sample calculation is shown for Factor B (pressure):
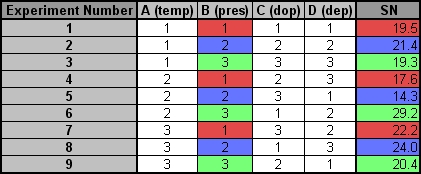
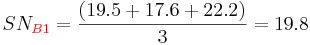
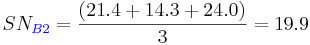
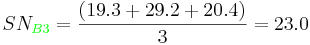
The effect of this factor is then calculated by determining the range:
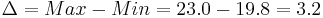
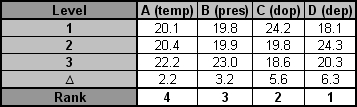
It can be seen that deposition rate has the largest effect on the processor yield and that temperature has the smallest effect on the processor yield.
NOTE: The data for the following example is not real, and details pertaining to microprocessor fabrication may not be completely accurate.
a) Solution:
You have just produced one thousand 55 gallon drums of sesame oil for sale to your distributors. However, just before you are to ship oil, one of your employees remembers that one of the oil barrels was temporarily used to store insecticide and is almost surely contaminated. Unfortunately, all of the barrels look the same.
One barrel of sesame oil sells for $1000, while each assay for insecticide in food oil costs $1200 and takes 3 days. Tests for insecticide are extremely expensive. What do you do?
Solution
Extreme multiplexing. This is similar to using a Taguchi method but optimized for very sparse systems and specific cases. For example, instead of 1000 barrels, let us consider 8 barrels for now, one of which is contaminated. We could test each one, but that would be highly expensive. Another solution is to mix samples from each barrel and test the mixtures.
- Mix barrels 1,2,3,4 ---> Sample A
- Mix barrels 1,2,5,6 ---> Sample B
- Mix barrels 1,3,5,7 ---> Sample C
We claim that from testing only these three mixtures, we can determine which of the 8 barrels was contaminated. Let us consider some possible results of these tests. We will use the following label scheme: +/-,+/-,+/- in order of A, B, C. Thus, +,-,+ indicates A and C showed contamination but not B.
- Possible Result 1: -,-,- The only barrel not mixed in was #8, so it is contaminated.
- Possible Result 2: +,-,- Barrel #4 appears in A, but not in B and C. Since only A returned positive, barrel #4 was contaiminated.
- Possible Result 3: -,+,- Barrel #6 appears in B, but not in A and C. Since only B returned positive, barrel #6 was contaminated.
We can see that we have 23 = 8 possible results, each of which corresponds to a particular barrel being contaminated. We leave the rest of the cases for the reader to figure out.
Solution with 1,000 barrels: Mix samples from each barrel and test mixtures. Each mixture will consist of samples from a unique combination of 500 barrels. Experiments required = log2(1000)=~10.
Solution with 1,000,000 barrels: Experiments required = log2(1000000)=~20.
Thus, by using extreme multiplexing, we can greatly reduce the # of experiments needed, since the # of experiments scales with log2(# of barrels) instead of # of barrels.
You are producing decaffeinated coffee using supercritical carbon dioxide as a solvent. To optimize the effectiveness of caffeine removal, you would like to test 2 different possible pressures of CO2, 3 possible temperatures, 3 ratios of CO2 to coffee beans, 3 residence times of supercritical CO2 with beans, and 2 different procedures for preroasting the beans prior to caffeine extraction. What is the most appropriate method to design your optimization experiments?
- Factorial design
- Taguchi methods
- Random design
- None of the above. Coffee should never be decaffeinated
- Answer
-
To perform a full factorial experiment, you’d need to account for: (2 pressures)(3 temperatures)(3 ratios)(3 times)(2 roasts) = 108 experiments! Thus, factorial design is not a practical choice: a good rule of thumb is 1-3 variables with few states for a manageable factorial analysis. However, selecting 3 for the number of levels and consulting the array selector, we see that an L18 array will suffice for a Taguchi analysis. 18 is a much more feasible number of experiments than 108. Finally, random design is only practical when >50 variables are involved and few will have significant impact on the system, which is not the case here. Thus, although the author is of the opinion that choice ‘D’ has significant merit, the correct answer is ‘B’.
Which of the following is inconsistent with the Taguchi philosophy of quality control?
- Variation is the opposite of quality
- Interactions between parameters affecting product quality are unimportant and should never be considered
- Customer dissatisfaction is the most important measure for process variation, and should be minimized
- A high signal to noise ratio (SN) should be present in a process to make it robust against uncontrollable factors that would cause variation
- Answer
-
Choice ‘A’ is another way of expressing point 3 of the Taguchi philosophy above. Similarly, choice ‘C’ is another way of expressing the cost function, and choice ‘D’ is consistent with philosophy 2. Although it is true that the Taguchi methods do not account well for interactions between variables, choice ‘B’ is incorrect for two reasons. 1) Pair-wise interactions between variables are accounted for in Taguchi orthogonal arrays. 2) Negligibility of interactions between parameters is not so much a central tenet of Taguchi philosophy as a necessary simplifying assumption. An analog is decoupling of MIMO systems. Since applying this assumption yields good results, it is consistent with Taguchi thinking to say that makes it valid.
References
- Vuchkov, I.N. and Boyadjieva, L.N. Quality Improvement with Design of Experiments: A Response Surface Approach. Kluwer Academic Publishers. Dordrecht, 2001.
- http://www.ee.iitb.ac.in/~apte/CV_PRA_TAGUCHI_INTRO.htm
- http://www.york.ac.uk/depts/maths/tables/orthogonal.htm
- www.freequality.org/sites/www_freequality_org/documents/tools/Tagarray_files/tamatrix.htm
- Roy, R. K., A Primer on the Taguchi Method, Van Nostrand Reinhold, New York 1990.
- Ravella Sreenivas Rao, C. Ganesh Kumar, R. Shetty Prakasham, Phil J. Hobbs (2008) The Taguchi methodology as a statistical tool for biotechnological applications: A critical appraisal Biotechnology Journal 3:510–523.


