3.1: Static Feedback Controller
- Page ID
- 24399
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Feedback Control System
The standard block diagram of a single-input single-output (SISO) feedback control system includes a plant, \(G(s)\), a controller, \(K(s)\), and a sensor, \(H(s)\), where \(H\left(s\right)=1\) is often assumed.
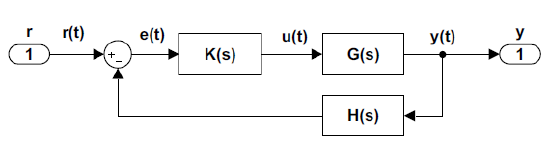
The overall system transfer function from input, \(r(t)\), to output, \(y(t)\), can be obtained by considering the error signal, \(e=r-Hy=r-KGHe\). Thus, \(\left(1+KGH\right)e=r\).
Let \(L\left(s\right)=KGH(s)\) denote the feedback loop gain; then, \(\left(1+L\right)e=r\).
The error transfer function from \(r\) to \(e\) is obtained as: \[S(s)=\frac{1}{1+L(s)}=\frac{1}{1+KGH(s)} \nonumber \]
The closed-loop transfer function from \(r\) to \(y\) is obtained as: \[T(s)=\frac{KG(s)}{1+KGH(s)} \nonumber \]
We may note that: \(S\left(s\right)+T\left(s\right)=1\).
Static Loop Controller Design
A static controller denotes the use of an amplifier with a gain, \(K\), to generate input to the plant, \(G(s)\). The controller action is represented as: \(u=Ke\), where \(e\) represents the error signal and \(u\) is the plant input.
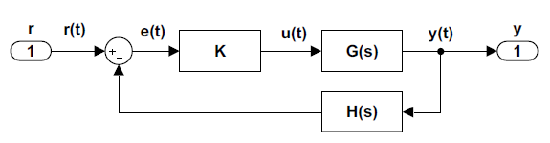
Assuming \(H(s)=1\), the closed-loop transfer function is given as:
\[\frac{y\left(s\right)}{r\left(s\right)}=T\left(s\right)=\frac{KG(s)}{1+KG\left(s\right)} \nonumber \]
Let \(G\left(s\right)=\frac{n\left(s\right)}{d\left(s\right)}\); then, the closed-loop transfer function is obtained as:
\[\frac{y\left(s\right)}{r\left(s\right)}=\frac{Kn\left(s\right)}{d\left(s\right)+Kn(s)} \nonumber \]
The closed-loop characteristic polynomial is defined as: \(\mathit{\Delta}\left(s,K\right)=d(s)+Kn\left(s\right)\).
From a controller design perspective, the gain \(K\) can be selected to achieve desirable root locations for the closed-loop characteristic polynomial. The design can be performed by comparing the coefficients of the characteristic polynomial with a desired characteristic polynomial.
The model for an environmental control system is given as: \(G\left(s\right)=\frac{1}{20s+1}\).
Assuming a static gain controller, the closed-loop characteristic polynomial is obtained as: \(\mathit{\Delta}\left(s,K\right)=20s+1+K\).
Suppose a desired characteristic polynomial is selected as: \({\mathit{\Delta}}_{des}\left(s\right)=4(5s+1)\). Then, by comparing the coefficients, we obtain the static controller as: \(K=3\).
The model for a position control system is given as: \(G\left(s\right)=\frac{1}{s\left(0.1s+1\right)}\).
Assuming a static gain controller, the characteristic polynomial is obtained as: \(\mathit{\Delta}\left(s,K\right)=s(0.1s+1)+K\).
Suppose a desired characteristic polynomial is selected as: \({\mathit{\Delta}}_{des}\left(s\right)=0.1(s^2+10s+50)\). Then, by comparing the coefficients, we obtain the static controller as: \(K=5\).
Example 3.2: