5.6: Controller Realization
- Page ID
- 24411
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Frequency Selective Filters
The dynamic controllers, including phase-lead, phase-lag, lead-lag, PD, PI, PID, represent frequency selective filters that may be realized by electronic circuits built with operational amplifiers and resistor-capacitor networks.
A resister-capacitor (RC) circuit connected in series or parallel has the following impedance:
Series RC circuit: \(Z_{\rm ser} (s)=R+\frac{1}{C\rm s} =\frac{RCs+1}{Cs}\)
Parallel RC circuit: \(Z_{\rm par} (s)=\frac{R/Cs}{R+\frac{1}{Cs} } =\frac{R}{RCs+1}\)
An operational amplifier (Op-Amp) in the inverting configuration has an input–output transfer function: \(\frac{V_{0} (s)}{V_\rm i (s)} =-\frac{Z_\rm f (s)}{Z_\rm i (s)} ,\) where \(Z_\rm i (s)\) and \(Z_\rm f (s)\) denote the input and feedback path impedance.
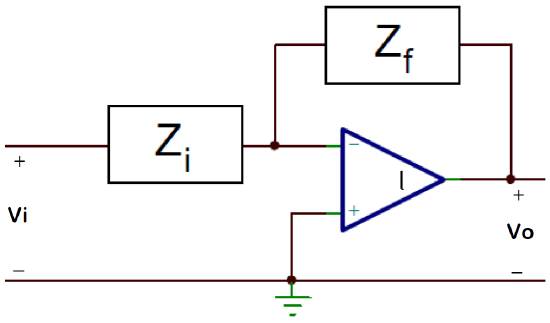
Phase-Lead/Phase-Lag Controllers
A first-order phase-lead or phase-lag controller can be realized with parallel RC circuits placed as input and feedback paths. The resulting controller transfer function is given as:
\[K(s)=-\frac{Z_\rm f (s)}{Z_\rm i (s)} =-\frac{R_{f} }{R_{i} } \frac{(R_\rm i C_\rm i s+1)}{(R_\rm f C_\rm f s+1)} . \nonumber \]
The controller transfer function has a zero located at: \(z_\rm c =\frac{1}{R_\rm i C_\rm i }\), and a pole at: \(p_\rm c =\frac{1}{R_\rm f C_\rm f }\).
Hence we may choose \(R_{\rm i} C_{\rm i} >R_{\rm f} C_{\rm f}\) for the phase-lead and \(R_{\rm i} C_{\rm i} <R_{\rm f} C_{\rm f}\) for the phase-lag design.
For static gain and sign correction, a resistive Op-Amp circuit can be employed. The circuit has a gain of: \(\frac{V_{\rm o} }{V_\rm i } =-\frac{R_{\rm f} }{R_{\rm i} } \).
Let \(K(s)=\frac{5(s+1)}{s+10}=\frac{0.5(s+1)}{0.1s+1}\); then, the transfer function realization involves the following constraints: \(R_{\rm i} C_{\rm i} =1,\; R_{\rm f} C_{\rm f} =0.1,\; R_{\rm f} /R_\rm i =0.5.\)
We may choose, for example, \(R_\rm i =100K\Omega\). Then, \(R_\rm f =50K\, \Omega ,\; C_\rm i =10\mu \, {\rm F},\; C_\rm f =2\mu \, {\rm F.}\;\)
PD, PI, PID Controllers
These controllers can be realized by combining the following impedance:
\[G_{\rm PD} (s)=-\frac{R_\rm f }{Z_{\rm par} (s)} =-\frac{R_\rm f }{R_\rm i } (R_\rm i C_\rm i s+1) \nonumber \]
\[G_{\rm PI} (s)=-\frac{1/C_\rm f s}{Z_{\rm par} (s)} =-\frac{1}{R_\rm i C_\rm f } \frac{(R_\rm i C_\rm i s+1)}{s} \nonumber \]
\[G_{\rm PID} (s)=-\frac{Z_{\rm f-ser} (s)}{Z_{\rm i-par} (s)} =-\frac{1}{R_\rm i C_\rm f } \frac{(R_\rm i C_\rm i s+1)(R_\rm f C_\rm f s+1)}{s} . \nonumber \]
For the PID controller, the controller gains are solved as functions of component values:
\[\rm k_\rm p =\frac{R_{\rm f} }{R_{\rm i} } +\frac{C_{\rm i} }{C_{\rm f} } ,\; \; k_\rm i =R_{\rm f} C_{\rm i},\; \; k_\rm d =\frac{1}{R_{\rm i} C_{\rm f} } \nonumber \]
Let \(G_{\rm PID} (s)=\frac{(s+0.1)(s+10)}{s}\); then, to realize the transfer function with RC networks, we may choose, for example:
\[R_{\rm i} =100\; {\rm K}\Omega ,\; R_{\rm f} =1{\rm M}\Omega ,\; C_{\rm i} =1\; \mu \, {\rm F},\; C_{\rm f} =10\; \mu \, {\rm F} \nonumber \]


