7.2: Four Questions
- Page ID
- 81506
When developing an accounting concept for a new property, there are four questions that must be answered. When applied to energy, the questions become
- What is energy?
- How can it be stored in a system?
- How can it be transported?
- How can it be created or destroyed?
Once we have answered these questions we will have the appropriate balance equation for energy.
7.2.1 What is energy?
From your study of basic mechanics, you have already been introduced to three types of energy — kinetic energy, gravitational potential energy, and spring (elastic) energy. Each of these mechanical energies followed naturally from a calculation of the mechanical work required to change the state of a system:
| Mechanical Energy | Property Changed |
|---|---|
| Kinetic energy, \(E_{K}\) | Translational velocity of a particle. |
| Gravitational potential energy, \(E_{G P}\) | Elevation of a particle in a gravitational field. |
| Spring energy, \(E_{\text {spring}}\) | Length of an elastic material. |
It also seemed reasonable to apply the accounting principle and combine mechanical energy and mechanical power in a mechanical energy balance: \[\frac{d}{dt} \left(E_{K}+E_{G}+E_{\text {Spring}}\right) = \dot{W}_{\text {mech}} \nonumber \] Unfortunately, this mechanical energy balance is only valid under certain restrictions.
Historically, the study of what we now call energy was divided into the study of heat and the study of work. The remnants of this division are still with us today. Common usage of these terms implies that heat is something a system has and can transfer, and work is something that a system does. One of the crowning achievements of 19th century physics was the recognition that these two concepts could be unified through the First Law of Thermodynamics, and that both represent mechanisms for transferring energy.
In our study of linear momentum, we had a very precise definition for the linear momentum of a particle and subsequently for a system. Unfortunately for the student, there is no single expression for energy because energy takes many different forms. Thus our understanding of energy will be based on a set of operational definitions that help us recognize it. (Although this may sound complicated, do not fret. In most applications, only a few easily recognizable forms of energy are involved. The operational definitions provide the foundation for understanding the concept, but are rarely required in daily practice.)
Thermodynamic Work
We have already explored mechanical work and learned how it may change a system. Many other interactions between a system and its surrounding can also affect a system in ways that mimic mechanical work. To investigate these effects requires a broader concept that includes mechanical work as a subset. This broader concept is called thermodynamic work. The operational definition for thermodynamic work is as follows:
Thermodynamic work is an interaction between a system and its surroundings that occurs in such a fashion that the only change in either the system or the surroundings could have been an increase in the gravitational potential energy of the system or the surroundings. The magnitude of the work equals the increase in the gravitational potential energy that could have occurred.
Note that this definition does not say that the gravitational potential energy of the system or surroundings did in fact increase. It says that it could have increased. Typically, we will just use the term work as a synonym for thermodynamic work. (We will decide shortly that this interaction is a transfer of energy; however, to state this now is logically premature.) Mechanical work is a subset of thermodynamic work. In general, we will not apply this definition directly once we have identified the common forms of work. However, it does serve a purpose when new interactions are studied.
Adiabatic Process, Boundary, and System
An adiabatic process is any process that involves only work interactions with the surroundings. An adiabatic boundary is a boundary that only allows work interactions with the surroundings. A system that only has adiabatic boundaries is called an adiabatic system.
First Law of Thermodynamics
After much experimentation, the First Law of Thermodynamics became an established fundamental principle in the latter half of the 19th century. One form of it says the following:
When any closed system undergoes an adiabatic process, the net work associated with the change of state is the same for all possible adiabatic processes that connect the same two equilibrium end states.
Because the amount of adiabatic work for a closed system only depends on knowing the two end states of the system, the adiabatic work for a closed system defines the change in a property for the system. This property is called the energy of the system and defined by the relation: \[\Delta E_{sys} = E_{sys, \ 2}-E_{sys, \ 1} = W_{1 \text{-} 2, \text { adiabatic}} \quad \text { for a closed system. } \nonumber \] Experience has shown that the adiabatic work required to change the state of a closed system depends on the amount of mass of the system; thus, energy is an extensive property.
The first law of thermodynamics can also be stated as two postulates:
- There exists an extensive property called energy, \(E\).
- The change in energy for a closed system between any two states is defined as the work done on the system during an adiabatic process connecting the two states, \(\Delta E = E_{2} - E_{1} = W_{1 \text{-} 2 \text{ adiabatic}}\).
This now provides us a way to calculate the change in energy for a closed system.
The dimensions of energy are the same as for work: \([\text{Force}][\text{Length}]\). Although the dimensions are the same, there are several units for energy that are commonly used by engineers. In the SI system, the standard unit is the joule \((\mathrm{J})\) where \(1 \mathrm{~J} = 1 \mathrm{~N} \cdot \mathrm{m}\). In the USCS system, there are two units that commonly occur: the foot-pound-force \((\mathrm{ft} \cdot \mathrm{lbf})\) and the British thermal unit \((\mathrm{Btu})\). The foot-pound-force had its birth in the study of mechanical work and the British thermal unit was used in the study of heat. One of the most famous results of physics was the experimental determination of the "mechanical equivalent of heat" by Joule. Today we know that the correct relationship between these two units of energy is approximately \[1 \mathrm{~Btu}=778.17 \mathrm{~ft} \cdot \mathrm{lbf} \nonumber \] One British thermal unit approximately equals the amount of energy required to raise the temperature of one pound-mass of liquid water one degree Fahrenheit at room temperature.
The first law of thermodynamics only tells us how to calculate the change in energy of a system. This is also a characteristic of the property energy — we can only calculate energy differences.
But what about kinetic energy and gravitational potential energy and spring energy? Can't we evaluate absolute values for these energies using our familiar equations? The answer is no. For example, the numerical value of the kinetic energy of a particle, \(m V^{2} / 2\), changes depending upon which inertial reference frame you choose when evaluating the velocity. Imagine you are throwing a baseball on a steadily moving train. If the velocity is measured with respect to the train the kinetic energy has one value; if the velocity is measured with respect to the ground, the kinetic energy will have a different value. Similar arguments can be made for gravitational potential energy and spring energy.
Following the same line of reasoning we used earlier with mechanical energy and mechanical work, it seems reasonable that we should interpret work as a mechanism for transporting energy across the boundary of a system. We will show shortly that work alone is insufficient to explain how the energy of a system can change.
7.2.2 How can energy be stored in a system?
Based on the first law of thermodynamics and the concept of thermodynamic work, we have a way to investigate changes in the energy of a closed system (see Eq. \(\PageIndex{1}\)). Fortunately, engineers and scientists have developed a fairly comprehensive picture of the various forms in which energy can be stored in a system.
Types of Energy
Energy can be stored in many forms. In addition to kinetic energy, gravitational potential energy, and elastic energy, there are several other types of energy. We will find it useful to classify the energy stored in a system \(E_{\text {sys}}\) into four groups: \[ E_{sys} = \underbrace{U}_{\begin{array}{c} \text{Internal} \\ \text{energy} \end{array}} + \underbrace{E_K}_{\begin{array}{c} \text{Translational} \\ \text{kinetic energy} \end{array}} + \underbrace{E_{GP}}_{\begin{array}{c} \text{Gravitational} \\\ \text{potential energy} \end{array}} + E_{other} \nonumber \]
where \(U\) is the internal energy of the system, \(E_{K}\) is the translational kinetic energy of the system, \(E_{G P}\) is the gravitational potential energy of the system, and \(E_{other}\) represents all other forms of energy. Two of these are familiar and two are not.
First, let's consider the familiar terms. The translational kinetic energy and the gravitational potential energy are the same ones we have used previously in this course and require no additional discussion. Notice that we have now been more explicit about the type of kinetic energy our system has. A rotating system with a stationary center of mass may still store energy as rotational kinetic energy. (Any piece of rotating machinery can store a significant amount of energy in its rotation. Containing this energy during a catastrophic failure of the device, e.g. the failure of a turbine blade or the failure of a tire rim, is often a major safety factor in the design of the device.)
Of the two new energies, the most important is the internal energy. The identification of internal energy was a direct consequence of the development of the first law of thermodynamics.
The internal energy of a substance is the extensive property that represents the microscopic kinetic and potential energy of the molecules and atoms that make up a substance.
Any object with mass has internal energy as a result of the "motions and configurations of its internal particles" (E. F. Obert and R. A. Gaggioli, Thermodynamics, 2nd Ed., McGraw-Hill, New York, 1963, pg. 18). Changes in the internal energy of a system are manifest by changes in other properties such as temperature, pressure, and density.
To give us some insight into how internal energy was discovered and what it is physically, consider the device shown in the figure. The device consists of a rigid tank that is heavily insulated. The tank contains air and a set of fan blades attached to a shaft. The other end of the shaft is attached to a pulley and suspended from the pulley by a cable is a mass.
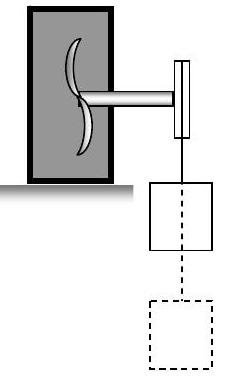
Figure \(\PageIndex{1}\): System consisting of fan blades inside a rigid container attached to a shaft and pulley, from which a mass is suspended outside the container.
Initially the fan-shaft-pulley-mass system is stationary. If the mass is allowed to fall a distance \(L\) and once again become stationary, what happens to the gas inside the tank?
You might suggest that the temperature of the gas might increase, and also its pressure. If you wait long enough the gas would also become stationary once again.
Since the energy of the closed system cannot change, the decrease in gravitational potential energy must be balanced by an increase in another form of energy.
If we examined a system that includes everything in the picture, we would discover two things:
(1) There is no interaction on the boundary of the system that qualifies as thermodynamic work. This is a direct consequence of the insulation. Thus, the energy of the system is constant.
(2) The gravitational potential energy of the system decreases.
For this system, the energy that increases is the internal energy of the tank walls, the fan blade and the portion of the shaft inside the tank. On a macroscopic level, this change in internal energy might manifest itself as an increase in the temperature of the system. On a microscopic level, we would observe changes in the motion of the atoms and molecules that form these objects; hence the name internal energy.
The interaction that occurs between the portion of the shaft outside the tank and the shaft inside the tank does in fact represent thermodynamic work (shortly we will identify it as shaft work). To justify this, imagine that the tank and its contents were replaced with a system containing a frictionless pulley and mass. Now the falling of the weight in the original system results in the raising of the imagined mass in a gravitational field with only an increase of the gravitational potential energy of the imagined system. This satisfies our definition of thermodynamic work. Note that in identifying thermodynamic work, it is not what actually happens to the energy transferred but what could happen
The remaining term \(E_{other}\) in our energy expression, Eq. \(\PageIndex{2}\), includes all other forms of energy. These may or may not be important depending upon the system being considered. Some of the most common forms of energy that can be stored in a system are listed below:
| Energy | Example |
|---|---|
| Elastic | Energy stored in the deformation of an elastic material, e.g. a spring. |
| Kinetic, Rotational | Energy stored in an object due to its rotation about an axis, e.g. a flywheel |
| Surface tension | Energy stored in the stretching of a liquid film, e.g. formation of a raindrop. |
| Electric field | Energy stored in an electric field, e.g. a capacitor |
| Magnetic field | Energy stored in a magnetic field, e.g. an inductor |
One of the major challenges in problem solving is deciding which forms of energy are important for a particular system. This list is not all inclusive. As you continue your education, you may discover other forms of energy that play a prominent role in specific physical phenomena.
Specific energy and the energy of a system
For our purposes, we will assume that the energy of the system is associated with the mass contained inside the system; thus, \[E_{\mathrm{sys}}=\int\limits_{V_{sys}} e \ \rho dV \nonumber \] where \(e\) is the energy per unit mass, or the specific energy, of the system. The dimensions of specific energy are \([\mathrm{Energy}]/[\mathrm{Mass}]\) and typical units are \(\mathrm{kJ} / \mathrm{kg}\) in SI and \(\mathrm{ft} \cdot \mathrm{lbf} / \mathrm{lbm}\) or \(\mathrm{Btu} / \mathrm{lbm}\) in USCS. Since energy is an extensive property, the energy of a system is equal to the sum of the energy of its subsystems. For some types of energy, the energy is actually stored in an electric or magnetic field that may or may not correspond with the physical mass of the system. This will require a different approach to assigning the energy of the system. Typically, we will assume that the energy is located within a specific physical device, such as a capacitor or inductor.
7.2.3 How can it be transported?
Energy can be transported across the boundary of a system by three different mechanisms — work, heat transfer, and mass transfer of energy.
Energy transport by work
Energy transport by work can occur at both flow and non-flow boundaries. Any interaction between a system and its surroundings that satisfies the definition of thermodynamic work is a work transfer of energy. The work transfer rate of energy into the system is also known as the power and has the same characteristics as mechanical power discussed earlier. Thinking of power as an energy transfer rate, we can write \[\dot{E}_{\text {work}} = \dot{W} \nonumber \] Subscripts "in" or "out" are often used to indicate the direction of the transfer. When we sum up the work transfer rates of energy for a system we will frequently report this as a net rate: \[\sum \dot{W}_{\text{in}} - \sum \dot{W}_{\text{out}} = \dot{W}_{\text{net, in}} = -\dot{W}_{\text{net, out}} \nonumber \] Notice how the subscripts are connected with the signs. This becomes especially important when you copy an equation from the text, because you must understand the sign convention observed to correctly use the derived equation.
There are many different units for work and power. The most common ones used in this course are presented below:
| SI System | USCS System | |
|---|---|---|
| Work |
newton-meter \((\mathrm{N} \cdot \mathrm{m})\) joule \((\mathrm{J})\) kilojoule \((\mathrm{kJ})\) |
foot-pound-force \((\mathrm{ft} \cdot \mathrm{lbf})\) British thermal unit \((\mathrm{Btu})\) |
| Power |
newton-meter/second \((\mathrm{N} \cdot \mathrm{m} /\mathrm{s})\) joule/second \((\mathrm{J} / \mathrm{s})\) watt \((\mathrm{W})\) kilowatt \((\mathrm{kW})\) |
foot-pound-force/second \((\text{ft-lbf} / \mathrm{s})\) British-thermal-unit/second \((\mathrm{Btu} / \mathrm{s})\) horsepower \((\mathrm{hp})\) |
There are many ways that energy can be transported across a non-flow boundary of a system by work. Consider the device shown in Figure \(\(\PageIndex{2}\) consisting of a battery connected to a DC motor that turns a paddle wheel that stirs a gas contained in a piston-cylinder device.
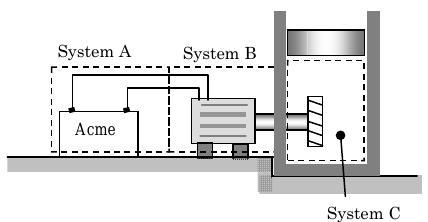
Figure \(\PageIndex{2}\): Examples of work transfer of energy.
Initially, everything in the device is stationary and the pressure of the gas in the piston-cylinder device is sufficient to "float" the piston. If we close a switch between the battery and the motor, what would happen? We would expect the motor to turn the paddle wheel and with time the piston would probably rise. (Take a minute and think about this. Would you expect the piston to rise?) Now what are the work transfers of energy for this system? Since work is defined in terms of transfers at a boundary, we will identify three systems \(A\), \(B\), and \(C\). From a work perspective, the battery (System \(A\)) does electrical work on the motor (System \(B\)). The motor does shaft work on System \(C\), the paddle wheel, shaft, and gas inside the cylinder. Finally, the gas does expansion work to move the piston. In the following sections, we will examine each of these work modes in more detail.
Compression-Expansion (P dV) Work
One of the most important and pervasive work modes is compression-expansion work. This is the work mode that occurs in your car engine as hot, high-pressure gas expands against the piston. As they expand, the gas does work on the piston. This work is then transferred through the connecting rod to the crankshaft to the transmission to the drive shaft through the differential to the axle and finally to the wheels of the car. (Whew, what a path!)
But let's get back to what is happening to the hot gas. Consider the simple piston-cylinder device shown in Figure \(\PageIndex{3a}\). The hot, high-pressure gas is contained in the closed volume formed by the piston and the cylinder walls. For clarity, let's consider the case of expansion where the piston is moving to the right. We are interested in finding the work done by the piston on the gas: \[W_{in} = \int\limits_{\mathrm{x}_{1}}^{\mathrm{x}_{2}} \mathbf{F}_{\text {surface}} \cdot d \mathbf{x} = \int\limits_{\mathrm{x}_{1}}^{\mathrm{x}_{2}}\left(-F_{\text {piston}} \mathbf{i}\right) \cdot(d x \mathbf{i}) = -\int\limits_{x_{1}}^{x_{2}} F_{\text {piston}} \cdot d x \nonumber \] where the only surface force that moves is \(F_{\text {piston}}\), the force that the piston exerts on the gas (See Figure \(\PageIndex{3b\)). Note that the minus sign in the equation comes about because the force acts opposite to the displacement direction.
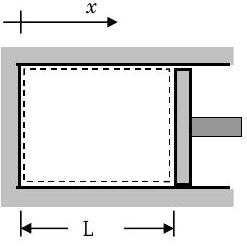 a) Piston-cylinder device
a) Piston-cylinder device.jpg?revision=1) b) Cylinder contents with piston force
b) Cylinder contents with piston forceThis is a perfectly good expression; however it would be more useful if it could be expressed in terms of the properties the gas inside the system. We can do this by rewriting Eq \(\PageIndex{6}\) in terms the average pressure at the piston-gas interface and the system volume: \[\begin{array}{l} W_{\text {in}} &= \displaystyle -\int\limits_{x_{1}}^{x_{2}} F_{\text {piston}} \cdot dx = -\int\limits_{x_{1}}^{x_{2}} \underbrace{\left(\frac{F_{\text {piston}}}{A_{\text {piston}}}\right)}_{=P_{\text {avg}}} \cdot \underbrace{A_{\text {piston}} \ dx}_{=dV} \\ &= \displaystyle -\int\limits_{V\kern-0.5em\raise0.3ex-_{sys, \ 1}} ^{V\kern-0.5em\raise0.3ex-_{sys, \ 2}} P_{\text {avg}} \cdot d V\kern-0.8em\raise0.3ex- \end{array} \nonumber \] Again note that to evaluate this equation only requires that we know the average pressure on the moving boundary of the system as a function of the system volume.
If we further assume that the expansion (or compression) process occurs slowly enough that the pressure within the system is uniform, then \(P_{\text {avg}}=P\), and the work on the gas during a compression-expansion process can be described by the equation: \[W_{\text {in}} = -\int\limits_{V\kern-0.5em\raise0.3ex-_{sys, \ 1}}^{V\kern-0.5em\raise0.3ex-_{sys, \ 2}} P \cdot d V\kern-1.0em\raise0.3ex- \quad \begin{aligned} &\text {Compression-Expansion (PdV) Work} \\ & \text {(Assumes spatially uniform pressure)} \end{aligned} \nonumber \] This work mode is commonly referred to as compression-expansion work or \(PdV\) work. When the system is compressed \((d V\kern-1.0em\raise0.3ex- < 0)\), the piston does work on the system and \(W_{\text {in}}>0\). When the system expands \((d V\kern-1.0em\raise0.3ex- >0)\), the system does work on the piston and \(W_{\text {in}}<0\) because energy is being transferred out of the system. This result is valid for both liquids and gases.
In practice, the basic equation for \(PdV\) work of a closed system must be integrated to determine the work for a process. Experience indicates that there are several processes that occur frequently and will be investigated here. As always you are warned against memorizing formulas. Focus on how the process assumption is used to integrate the basic equation for \(PdV\) work.
Constant-Volume Process: \(V\kern-1.0em\raise0.3ex- = V\kern-1.0em\raise0.3ex-_{1} = V\kern-1.0em\raise0.3ex-_{2}=C, \text{ a constant}\) \[W_{PdV, \text { in}} = -\int\limits_{1}^{2} P \ d V\kern-0.8em\raise0.3ex- = -\int\limits_{1}^{2} P \ \cancel{ d V\kern-0.8em\raise0.3ex- }^{=0} = 0 \nonumber \]
Constant-Pressure (Isobaric) Process: \(P=P_{1}=P_{2}=C, \text{ a constant}\) \[W_{PdV, \text { in}} = -\int\limits_{1}^{2} P \ d V\kern-1.0em\raise0.3ex- = -\int\limits_{1}^{2} C \ d V\kern-1.0em\raise0.3ex- = - C\left(V\kern-1.0em\raise0.3ex-_{2} - V\kern-1.0em\raise0.3ex-_{1}\right) = -P\left(V\kern-1.0em\raise0.3ex-_{2} - V\kern-1.0em\raise0.3ex-_{1}\right) \nonumber \]
Polytropic Process: \(P V\kern-1.0em\raise0.3ex-^{n} = P_{1} V\kern-1.0em\raise0.3ex-_{1}{ }^{n} = P_{2} V\kern-1.0em\raise0.3ex-_{2}{ }^{n}=C, \text{ a constant}\)
\[W_{PdV, \text{ in}} = -\int\limits_{1}^{2} P \ d V\kern-1.0em\raise0.3ex- = -\int\limits_{1}^{2} \left(\frac{C}{V\kern-0.8em\raise0.3ex-^{n}}\right) d V\kern-0.8em\raise0.3ex- \nonumber \]
If \(n=1\):
\[W_{PdV, \text { in}} = -\int\limits_{1}^{2} P \ d V\kern-1.0em\raise0.3ex- = -\int\limits_{1}^{2} \left(\frac{C}{V\kern-0.8em\raise0.3ex-}\right) d V\kern-1.0em\raise0.3ex- = -C \int\limits_{1}^{2} \frac{d V\kern-0.8em\raise0.3ex-}{V\kern-0.8em\raise0.3ex-} = -C \ln \left(\frac{V\kern-0.8em\raise0.3ex-_{2}}{V\kern-0.8em\raise0.3ex-_{1}}\right) = -P V\kern-0.8em\raise0.3ex- \ln \left(\frac{ V\kern-0.8em\raise0.3ex- _{2}}{ V\kern-0.8em\raise0.3ex- _{1}}\right) \nonumber \]
If \(n \neq 1\):
\[ \begin{align*} W_{PdV, \text { in}} &= -\int\limits_{1}^{2} P \ d V\kern-1.0em\raise0.3ex- = -\int\limits_{1}^{2} \left(\frac{C}{V\kern-0.8em\raise0.3ex-^{n}}\right) d V\kern-1.0em\raise0.3ex- = -C \int\limits_{1}^{2} V\kern-1.0em\raise0.3ex-^{-n} \ d V\kern-0.8em\raise0.3ex- \\ &= -C\left[\frac{V\kern-0.8em\raise0.3ex-^{-n+1}}{-n+1}\right]_{V\kern-0.5em\raise0.3ex-_{1}}^{V\kern-0.5em\raise0.3ex-_{2}} = -C \left[\frac{V\kern-1.0em\raise0.3ex-_{2}{ }^{1-n} - V\kern-1.0em\raise0.3ex-_{1}{ }^{1-n}}{1-n}\right] = C\left[\frac{V\kern-1.0em\raise0.3ex-_{2}{ }^{1-n} - V\kern-1.0em\raise0.3ex-_{1}{ }^{1-n}}{n-1}\right] \\[4pt] &=\left[\frac{C V\kern-1.0em\raise0.3ex-_{2}{ }^{1-n} - C V\kern-1.0em\raise0.3ex-_{1}{ }^{1-n}}{n-1}\right] = \left[\frac{\left(P_{2} V\kern-1.0em\raise0.3ex-_{2}{ }^{n}\right) V\kern-1.0em\raise0.3ex-_{2}{ }^{1-n} - \left(P_{1} V\kern-1.0em\raise0.3ex-_{1}{ }^{n}\right) V\kern-1.0em\raise0.3ex-_{1}{ }^{1-n}}{n-1}\right] = \frac{\left(P_{2} V\kern-1.0em\raise0.3ex- _{2} - P_{1} V\kern-1.0em\raise0.3ex- _{1}\right)}{n-1} \end{align*} \nonumber \]
Starting at the same initial state 1, plot a constant volume process, a constant pressure process, and a polytropic process with \(n=1\) on a graph of \(P \text{ vs. } V\). How is \(W_{PdV}\) related to the area under the \(PV\) curve for each process?
 a) Looking into the system at a cut shaft
a) Looking into the system at a cut shaft.jpg?revision=1) b) End view of cut shaft
b) End view of cut shaft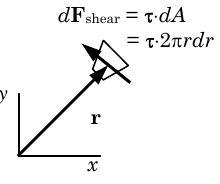.jpg?revision=1)
Shaft Work
When a portion of a system boundary is rotating, mechanical work is done on the system by shear forces at the rotating surface. The most common case of this is when a system boundary intersects (cuts) a rotating shaft (See Figure \(\PageIndex{4}\)). To calculate the mechanical work, we must identify the surface forces and their motion. Figure \(\PageIndex{4a}\) shows a system boundary that intersects a shaft. Figure \(\PageIndex{4b}\) shows the cross-section of the shaft and the direction of rotation as viewed looking into the system. Figure \(\PageIndex{4c}\) shows the differential force shearing force \(d \mathbf{F}_{shear}\) acting on the cut shaft and the position vector \(\mathbf{r}\) where it is applied. The mechanical work done on the rotating shaft inside the system is evaluated as \[W_{\text {shaft, in}} = \int\limits_{\theta_{1}}^{\theta_{2}} \int_{Ac} \underbrace{(\tau \ dA)}_{dF_{shear}} \underbrace{(r \ d \theta)}_{ds} = \int\limits_{\theta_{1}}^{\theta_{2}} \underbrace{\left[\int_{0}^{R} \tau(2 \pi r) r \ dr\right]}_{M_{0}=\text {moment about axis } 0} d \theta = \int\limits_{\theta_{1}}^{\theta_{2}} M_{0} \cdot d \theta \nonumber \] where \(M_{0}\) is the moment of the couple formed by all the shear forces acting on the cut shaft and \(\theta\) is the angular rotation of the shaft expressed in radians. If the shaft rotation (looking into the system) has the same sense as the moment applied to the system, \(W_{\text {shaft, in}}>0\). If the sense of the moment and shaft rotation are opposite, \(W_{\text {shaft, in}}<0\).
The shaft power is calculated using the equation: \[\dot{W}_{\text {shaft, in}}=M_{0} \cdot \omega \nonumber \] where \(\omega\) is the rotational speed in radians per second \((\mathrm{rad} / \mathrm{s})\) at the boundary. For most systems with rotating shafts, the shaft power is of more interest than the shaft work.
Electrical work and power
Energy can be transferred to a system by electric charge flowing through a system. When a charge is moved within an electric field a force is exerted on the charge (Figure \(\PageIndex{5}\)). When the charge is moved within the field, work is done on the charge. This situation is analogous to our earlier experience with a moving mass in a gravitational field.
.png?revision=1)
Figure \(\PageIndex{5}\): A charged particle moving in an electric field.
For a particle moving in a gravitational field we found that \[W_{\text {mech}}=\Delta E_{K}+\Delta E_{G P} \quad \text { and } \quad \Delta E_{GP} = m \Delta e_{GP}=m g \Delta z \nonumber \] In an analogous manner, the work done to move a charged particle with charge \(q\) in an electric field equals \[W_{\text {electric}}=\int\limits_{1}^{2} q \ dV = q\left(V_{2-0} - V_{1-0}\right) \nonumber \] where \(V_{i-0}\) is the electric potential at point \(i\). The electric potential is the mechanical work per unit charge required to move a charged particle in a stationary electric field between a reference point \(O\) and arbitrary point \(i\). The standard unit for electric potential is the volt (V), where 1 volt = 1 joule/coulomb \((1 \mathrm{~V}=1 \mathrm{~J} / \mathrm{C})\). As with any mechanical work, the electric work may be positive or negative.
In many applications, the problem is a system where an electric current is flowing across the boundary. In a typical configuration, electric current flows through the system at a known rate with no accumulation inside the system, see Figure \(\PageIndex{6}\). The electric potential on the boundary where the current crosses the system boundary is known with respect to a common ground. Under these conditions, the instantaneous electric power into the system is \[\dot{W}_{\text {electric, in}} = i \cdot\left(V_{\text {in-o =}} - V_{\text {out-o}} \right) \quad \text { Electric Power } \nonumber \] where \(i\) is the electric current crossing the boundary and the electric potential at the points on the boundary where the electric current enters and leaves the system are \(V_{\text {in-o}}\) and \(V_{\text {out-o}}\), respectively. When the electric potential decreases in the direction of the current flow, the electric power in is positive. When the electric potential increases in the direction of current flow, the electric power in is negative.
An example showing how the direction current flow influences the electric power for a simple dc battery is shown in Figure \(\(\PageIndex{6}\). When the battery is charging, energy is being added to the battery and the electric power in is positive. When the battery is discharging through a resistor, energy is leaving the battery and the electric power into the battery is negative. What would be the direction and the magnitude for the electric power for the resistor?
.png?revision=1)
Figure \(\PageIndex{6}\): Electric power for a 1.5-volt battery.
Flow work and power
At flow boundaries, the mass flowing into the system serves to compress the mass already inside the open system. This type of work is known as flow work and the rate of doing flow work is known as flow power. The flow power for a system is written as \[\begin{array}{l} \dot{W}_{\text {flow, net in}} &= \displaystyle \sum_{\text{in}} \dot{W}_{\text {flow, in}} - \sum_{\text{out}} \dot{W}_{\text {flow, out}} \\ &= \displaystyle \sum_{\text{in}} \dot{m}_{i} \left(P_{i} \nu_{i}\right) - \sum_{\text{out}} \dot{m}_{e} \left(P_{e} \nu_{e}\right) \end{array} \nonumber \] where \(P \nu\), the product of pressure and specific volume, is the specific flow work evaluated at the boundary where the mass flow occurs. A detailed development of this term will be delayed until later. Note that for a closed system, there is no mass flow rate and thus no flow power. Flow work is a mechanism for transferring energy that only occurs in open systems.
Work and power for a system
When we combine the expressions for the work transfer rates, the power, for a system we have the following expression: \[\begin{array}{ll} \dot{E}_{\text {work, net in}} &= \displaystyle \underbrace{ \left[\sum \dot{W}_{\text {in}} - \sum \dot{W}_{\text {out}}\right] }_{\begin{array}{c} \text {Rate of energy transfer by work} \\ \text {(excluding flow work)} \\ \text{(Power)} \end{array}} &+ \quad \displaystyle \underbrace{ \left[\sum_{\text{in}} \dot{m}_{i} \left(P_{i} \nu_{i}\right) - \sum_{\text {out}} \dot{m}_{e} \left(P_{e} \nu_{e}\right)\right] }_{\begin{array}{c} \text {Rate of energy transfer by flow work} \\ \text{(Flow Power)} \end{array}} \\ &= \quad\quad\quad \dot{W}_{\text{net, in}} &+ \displaystyle \quad \left[\sum_{\text{in}} \dot{m}_{i}\left(P_{i} v_{i}\right) - \sum_{\text{out}} \dot{m}_{e} \left(P_{e} v_{e}\right)\right] \end{array} \nonumber \] where \(P\) is the pressure and \(\nu\) is the specific volume at the boundary where the flow occurs. You should recognize that there may be several different types of work (or power) that are included in this term, e.g. an electric motor has both shaft work and electrical work.
Energy transport with mass flow
At flow boundaries, every lump of mass that enters or leaves the system carries with it some amount of energy. The rate at which energy is carried across a boundary is the product of the mass flow rate and the specific energy, \(e\), of the mass at the boundary: \[\dot{E}_{\text {mass flow}}=\dot{m} e \nonumber \] The net rate at which energy is carried into a system by mass flow is \[\dot{E}_{\text {mass flow, net in}} = \sum_{\text {in}} \dot{m}_{i} e_{i}-\sum_{\text {out }} \dot{m}_{e} e_{e} \nonumber \]
Energy transport by heat transfer
Heat transfer is the third and final mechanism for transferring energy across the boundary of a system. Heat transfer is any transfer of energy that cannot be classified as an energy transfer with mass flow or an energy transfer by work. Using the first law of thermodynamics and thermodynamic work, heat transfer for a closed system is precisely defined by the equation: \[Q_{1-2, \text {net in}} \equiv \left(E_{\text{sys}, \ 2}-E_{\text{sys}, \ 1}\right)-W_{1-2, \text {net in}} \nonumber \] This says that when a closed system undergoes a process, any process, between states 1 and 2, the difference between the change in energy of the system and the net work into the system equals the heat transfer for the system.
Just like work, heat transfer has both a rate form and a finite time form: \[Q_{1-2} = \int\limits_{t_{1}}^{t_{2}} \dot{Q} \ dt = \int\limits_{1}^{2} \delta Q \nonumber \] Also like work, heat transfer is a path function and has no value at a specified state. The heat transfer \(Q_{1 - 2}\), like work \(W_{1 - 2}\), can only be calculated once you know the path, the process, and the end states. We will use the same sign convention as used previously with other energy transfers. The use of subscripts, \(Q_{\text{in}}\) or \(Q_{\text {out}}\), is encouraged to avoid confusion.
Our experience tells us that heat transfer is closely related to the idea of temperature. For example, imagine that I have two rectangular blocks of copper. One has been sitting in an ice bath and the other has been sitting in a pot of boiling water. You could easily recognize which block is hot and which block is cold. Now suppose I place these two blocks in contact and then heavily insulate the touching blocks with some fiberglass insulation. Given sufficient time, you would discover that neither block is hot or cold-they are the same. We would commonly say that "the two blocks are at the same temperature." Alternatively, we might say the blocks had reached thermal equilibrium. What happened to the blocks? How did they interact? Again, you would probably say "the cold one heated up" and "the hot one cooled down."
This may be a correct layman's interpretation, but how does this fit into our energy picture? If you carefully consider how the two blocks interacted during the process and how they could interact with the surroundings, you will discover that there was no work transfer of energy or mass transfer of energy. All that remains to transfer energy is heat transfer, and that is what happened. The two blocks reached thermal equilibrium — a state where the temperature is spatially uniform and unchanging with time — by exchanging energy by heat transfer. This highlights another important characteristic of heat transfer — heat transfer will not occur between two systems in thermal equilibrium.
Our experience also tells us that heat transfer only occurs spontaneously from a region of high temperature to a region of low temperature. (Would you have expected the hot block of copper to get warmer and the cold block of copper to get cooler?)
The idea of temperature is so closely involved with heat transfer that the following definition is often given for heat transfer:
Heat transfer is a mechanism for transferring energy across the boundary of a system due to a temperature difference
There are three physical mechanisms for transporting energy by heat transfer — conduction heat transfer, convection heat transfer, and radiation heat transfer. We will revisit these three later, but an entire course on heat transfer is a required component of many curricula. E.g., mechanical engineering requires a complete course, and electrical and computer engineers will learn about specific applications to the cooling of electrical systems.
Heat transfers of energy may occur at any system boundary, although heat transfer at flow boundaries is usually neglected and is insignificant when compared to the transfer at non-flow boundaries. Symbolically, this can be written as \[\dot{E}_{\text {heat transfer, net in}}=\dot{Q}_{\text {net, in}} \nonumber \] Although only a single heat transfer term appears, the total heat transfer rate can be found by summing the heat transfer rates at all boundaries of the system.
How can energy be created or destroyed?
The First Law of Thermodynamics, one of the bedrock principles of physics, is really a statement that energy cannot be created or destroyed. Thus, energy is conserved!
As with species accounting earlier, if you only count one type of energy, such as mechanical energy, it appears that a specific energy can be created and destroyed. However, this only occurs because you are counting one only type of energy. Experience has repeatedly shown that when all forms of energy are accounted for, energy is conserved. In fact, our belief in this law is so complete that physicists have discovered new particles when they tried to understand why their experiments did not conserve energy.
7.2.5 Putting it all together — Conservation of Energy
Applying the accounting framework to energy, we know that \[\frac{d E_{\text {sys}}}{d t} = \dot{E}_{\text {work, net in}} + \dot{E}_{\text {heat transfer, net in}} + \dot{E}_{\text {mass flow, net in}} \nonumber \] Now, collecting all of the results developed above, we have an initial version of the rate form of the conservation of energy:
\[ d E_{\text{sys}} = \underbrace{ \dot{W}_{\text{net, in}} + \left[ \sum_{\text{in}} \dot{m}_i \left(P_i \nu_i\right) - \sum_{\text{out}} \dot{m}_e \left(P_e \nu_e\right) \right] }_{\begin{array}{c} \text{Net rate of} \\ \text{energy transport} \\ \text{by work} \end{array}} + \underbrace{ \dot{Q}_{\text{net, in}} }_{\begin{array}{c} \text{Net rate of} \\ \text{energy transport} \\ \text{by heat transfer} \end{array}} + \underbrace{ \left[ \sum_{\text{in}} \dot{m}_i e_i - \sum_{\text{out}} \dot{m}_e e_e \right] }_{\begin{array}{c} \text{Net rate of} \\ \text{energy transport} \\ \text{by mass flow} \end{array}} \nonumber \]
Although this result is perfectly acceptable, we will find it advantageous to combine all of the terms that involve mass flow before we write a final equation.
Energy, enthalpy and the mass flow terms
If we group the mass flow terms together, we have the following: \[\frac{d E_{\text {sys}}}{dt} = \dot{W}_{\text {non-flow, net in}} + \dot{Q}_{\text {net, in}} + \underbrace{\left[\sum_{\text {in}} \dot{m}_{i} \left(e_{i}+P_{i} v_{i}\right) - \sum_{\text {out}} \dot{m}_{e} \left(e_{e}+P_{e} v_{e}\right) \right]}_{\text{Mass flow terms}} \nonumber \] For many problems, we discover that there are only three types of energy that are important to consider — internal energy, translational kinetic energy, and gravitational potential energy. Writing this in terms of specific energy we have \[e = \frac{E}{m} = u + e_{K} + e_{G} = u+\frac{V^{2}}{2}+g z \nonumber \] where \(u\) is the specific internal energy, \(V^{2} / 2\) is the specific translational kinetic energy, and \(g z\) is the specific gravitational potential energy.
If we now substitute this back into the mass flow terms we can regroup the terms as \[\begin{array}{l} \dot{m}(e+P \upsilon) &= \dot{m} \left[\left(u+\dfrac{V^{2}}{2}+g z\right)+P \upsilon\right] \\ &= \dot{m} \left[(u+P \upsilon)+\dfrac{V^{2}}{2}+g z\right] \end{array} \nonumber \] Because the group of terms \(u+P \upsilon\) always shows up together in the energy balance, it is useful to give them a name. To do this we define a new extensive property called enthalpy (pronounced en-thal’-py), defined as the sum of the internal energy and the product of pressure and volume: \[H=U+P V \nonumber \] The specific enthalpy is defined similarly as follows: \[h=\frac{H}{m}=u+P \upsilon \nonumber \] As you might surmise, the units for enthalpy are the same as for energy, \(\mathrm{kJ}\) or \(\mathrm{Btu}\) or \(\mathrm{ft} \cdot \mathrm{lbf}\), and the units for specific enthalpy are the same as for specific internal energy, \(\mathrm{kJ} / \mathrm{kg}\) or \(\mathrm{Btu} / \mathrm{lbm}\) or \(\mathrm{ft} \cdot \mathrm{lbf} / \mathrm{lbm}\).
Using these results, the mass flow terms can be written more concisely as follows in terms of the specific enthalpy, the specific kinetic energy, and the specific gravitational potential energy: \[\dot{m} \left[(u+P \upsilon) + \frac{V^{2}}{2}+g z\right]=\dot{m}\left(h+\frac{V^{2}}{2}+g z\right) \nonumber \]
Rate form of the conservation of energy
We are now ready to write the rate-form of the conservation of energy equation in the form we find most useful: \[\frac{d E_{\text {sys}}}{d t} = \dot{W}_{\text {net, in}} + \dot{Q}_{\text {net, in}} + \left[\sum_{\text {in}} \dot{m}_{i}\left(h_{i}+\frac{V_{i}^{2}}{2}+g z_{i}\right) - \sum_{\text {out}} \dot{m}_{e} \left(h_{e} + \frac{V_{e}^{2}}{2}+g z_{e}\right)\right] \nonumber \] where the power term only excludes the flow power that is included in the mass flow rate terms. This is the most general form of the conservation of energy equation that we will be using and is the place to start all problems involving energy. Note that we have made some important assumptions in the types of energy that can be transferred with mass; however, experience indicates that these are sufficient for most problems. Also recognize that for a closed system, the mass flow rates are zero and the term in brackets disappears.
Conservation of Energy and the Work-Energy Principle
Conservation of Energy and the Work-Energy Principle for a Particle
The work-energy principle for a particle provides the same information as writing conservation of linear momentum for a particle. In developing the work-energy principle for a particle, we considered a particle moving in a gravitational field subject to a net surface force \(\mathbf{R}\). After a series of well-defined mathematical operations, we obtained the work-energy principle for a particle:
\[\begin{aligned} \text { Rate form: } &\quad \frac{\mathrm{d}}{\mathrm{dt}} \left( \underbrace{\mathrm{m} \frac{\mathrm{V}^{2}}{2}}_{\begin{array}{c} \text { Kinetic } \\ \text { energy } \end{array}} + \underbrace{mgz}_{\begin{array}{c} \text {Gravitational} \\ \text {potential} \\ \text {energy} \end{array}} \right) = \underbrace{\mathbf{R} \cdot \mathbf{V}}_{\begin{array}{c} \text {mechanical} \\ \text {power into} \\ \text {the system} \end{array}} \quad\quad \text{ or } \quad\quad \boxed{ \frac{d}{dt} \left(E_K + E_G\right) = \dot{W}_{\text{mech, in}} } \\ \text{ Finite-time form:} &\quad \Delta\left(m \frac{V^{2}}{2}\right) + \Delta(mgz) = \int\limits_{t_{1}}^{t_{2}} \mathbf{R} \cdot \mathbf{V} \ dt = \int\limits_{1}^{2} \mathbf{R} \cdot d \mathbf{s} \quad\quad \text { or } \quad\quad \boxed{ \Delta E_K + \Delta E_G = W_{\text{mech, in}} } \end{aligned} \nonumber \]
The work-energy principle states that the mechanical work done by the net surface forces on a particle equals the change in the kinetic energy and gravitational potential energy of the particle. Writing the conservation of energy for a particle we obtain the following: \[ \begin{aligned} \text { Rate form: } &\quad \frac{d}{dt} \left(U_{\text {sys}} + E_{K, \text { sys}} + E_{G, \text { sys}}\right) = \dot{Q}_{\text {net, in}} + \dot{W}_{\text {net, in}} \\[4pt] \text { Finite-time form: } &\quad \Delta U_{\text {sys}} + \Delta E_{K, \text { sys}} + \Delta E_{G, \text { sys}} = Q_{\text {net, in}} + W_{\text {net, in}} \end{aligned} \nonumber \] Examining the two sets of equations, we see that the conservation of energy equation reduces to the work-energy principle for a particle under two different conditions:
- Condition (1): The rate of change of the internal energy of the particle equals the net transport rate of energy into the particle by heat transfer, \(d U_{\text {sys}} / dt = Q_{\text {net, in}}\)
- Condition (2): The internal energy of the particle is constant, \(du_{\text {sys}} / dt = 0\), and the particle is adiabatic, \(\dot{Q}_{\text {net, in}}=0\).
To determine if condition (1) is satisfied requires information about the material substance that makes up the particle. Typically, condition (2) would be satisfied under conditions with no intentional heat transfer and no way to dissipate mechanical energy—that is, no friction—inside the system.
Conservation of Energy and the Work-Energy Principle for a System of Particles
If we had a system that contained \(n\) particles and we applied the work-energy principle for a particle individually to each particle, we would have for particle \(i\) \[\frac{d}{dt} \left(E_{K, \ i} + E_{G, \ i}\right)=\mathbf{R}_{i} \cdot \mathbf{V}_{i} \nonumber \] If we summed this equation up over the \(n\) particles in our system, we would obtain the following:
\[ \begin{gathered} \sum_{i=1}^{n} \left[ \frac{d}{dt} \left( E_{K, \ i} + E_{G, \ i} \right) \right] = \frac{d}{dt} \underbrace{ \left[ \sum_{i=1}^{n} \left(E_{K, \ i} + E_{G, \ i}\right) \right] }_{E_{K, \ sys} + E_{G, \ sys}} = \sum_{i=1}^{n} \underbrace{ \left[\mathbf{R}_i \cdot \mathbf{V}_i\right] }_{\dot{W}_{mech, \ in, \ i}} \\[4pt] \boxed{\frac{d}{dt} \left(E_{K, \ sys} + E_{G, \ sys}\right) = \sum_{i=1}^{n} \dot{W}_{mech, \ in, \ i}} \\[4pt] \text{where } \sum_{i=1}^{n} \dot{W}_{mech, \ in, i} \neq \underbrace{ \left( \sum_{i=1}^{n} \mathbf{R}_i \right) }_{\begin{array}{c} \text{Net surface force} \\ \text{acting on the} \\ \text{system of particles} \end{array}} \cdot \underbrace{ \left( \frac{1}{m_{sys}} \sum_{i=1}^{n} m_i \mathbf{V}_i \right) }_{\begin{array}{c} \text{Velocity of the center of mass} \\ \text{of the system of particles} \end{array}} \end{gathered} \nonumber \]\
The boxed equation is the work-energy principle for a system of particles. It looks much like the original work-energy principle for a particle; however, the mechanical power term on the right is the summation of the mechanical work done by surface forces on each particle. It is not equal to the dot product of the net surface force on the system of particles and the velocity of the center of mass of the system. This is a significant difference and failure to recognize this can lead to a serious misuse of the work-energy principle.
If we now write the conservation of energy equation for a closed system of particles and assume only kinetic, gravitational potential, and internal energies are important, we have the following: \[\begin{gathered} \frac{dE_{sys}}{dt} = \dot{Q}_{net, \ in} + \dot{W}_{net, \ in} + \cancel{ \sum_{in} \dot{m_i} \left(h_i + \frac{V_{i}^{2}}{2} + gz_{i} \right) - \sum_{in} \dot{m_e} \left(h_e + \frac{V_{e}^{2}}{2} + gz_{e}\right) }^{=0} \\[4pt] \boxed{ \frac{d}{dt} \left(U_{sys} + E_{K, \ sys} + E_{G, \ sys}\right) = \dot{Q}_{net, \ in} + \dot{W}_{net, \ in} } \end{gathered} \nonumber \]
Now if we subtract the work-energy principle for a system of particles from the conservation of energy principle for the system of particles we have the following:
\[ \begin{gathered} \left[ \frac{d}{dt} \left(U_{sys} + E_{K, \ sys} + E_{G, \ sys}\right) = \dot{Q}_{net, \ in} + \dot{W}_{net, \ in} \right] - \left[ \frac{d}{dt} \left(E_{K, \ sys} + E_{G, \ sys}\right) = \sum_{i=1}^{n} \dot{W}_{mech, \ in, \ i} \right] = \\[4pt] \underbrace{\frac{dU_{sys}}{dt}}_{\begin{array}{c} \text{Time rate of change} \\ \text{of the internal energy} \\ \text{within our system} \end{array}} = \underbrace{\dot{Q}_{net, \ in}}_{\begin{array}{c} \text{Heat transfer rate} \\ \text{for the system} \end{array}} + \underbrace{\dot{W}_{net, \ in}}_{\begin{array}{c} \text{Rate that work} \\ \text{is done by surface} \\ \text{forces acting on the} \\ \text{boundary of our system} \end{array}} - \underbrace{\sum_{i=1}^{n} \dot{W}_{mech, \ in, \ i}}_{\begin{array}{c} \text{Rate that work} \\ \text{is done by surface} \\ \text{forces acting on each} \\ \text{particle inside our system} \end{array}} \end{gathered} \nonumber \]
As with a single particle, the net work done on our system of particles by the surface forces acting on the system boundary only equals the sum of the mechanical work done by the surface forces acting on each of the particles under two conditions:
- Condition (1): The rate of change of the internal energy of the system of particles equals the net transport rate of energy into the system of particles by heat transfer, \(dU_{\mathrm{sys}} / dt=\dot{Q}_{\text {net, in}}\), or
- Condition (2): The internal energy of the system of particles is constant, \(dU_{\text {sys}} / dt=0\), and the particle is adiabatic, \(\dot{Q}_{\text {net, in}}=0\).
To validate condition (1) requires additional knowledge about the material substance of the particles. Typically, condition (2) occurs when the closed system of particles has three characteristics: (1) each particle in the system is incompressible, (2) there is no purposeful heat transfer, and (3) there is no friction of any kind within the system, e.g. particles can only deform elastically and there is no friction between particles. Friction on the system boundary is not prohibited; however, there can be no friction inside the system.
Counting Mechanical Energy for a Closed System
Starting with the rate-form of the conservation of energy for a closed system, \[\frac{dE_{sys}}{dt} = \dot{Q}_{net, \ in} + \dot{W}_{net, \ in} \nonumber \] Expanding the system energy and identifying mechanical forms of energy, we get \[\frac{d}{dt} \left( U + \underbrace{E_{k}+E_{G}+E_{spring}}_{\text{mechanical}} \right) = \dot{Q}_{\text {net, \ in}} + \dot{W}_{\text {net, \ in}} \nonumber \] Because, the mechanical forms are extensive properties, we may rearrange this equation in light of an accounting principle for mechanical energy:
\[ \frac{d}{dt} \underbrace{ \left(E_{k}+E_{G}+E_{spring}\right) }_{\begin{array}{c} \text{Rate of change of the} \\ \text{mechanical energy in} \\ \text{the system} \end{array}} = \underbrace{ \dot{W}_{net, \ in} }_{\begin{array}{c} \text{Transport rate} \\ \text{of energy} \\ \text{by work} \end{array}} + \underbrace{ \left[ \dot{Q}_{net, \ in} - \frac{dU}{dt} \right] }_{\begin{array}{c} \text{Rate of production} \\ \text{of mechanical energy} \\ \text{within the system} \end{array}} \nonumber \]
The left-hand side can now be interpreted as the rate of change of the mechanical energy in the system. The right-hand side contains two terms: the net work-transport rate of energy into the system and the production rate of mechanical energy within the system. This does not violate the general conservation of energy principle because we are only counting one form of energy.
Experience has shown that the term in brackets on the right-hand side, the production term, can be either positive or negative. This term is identically equal to zero if our closed system is (1) composed of incompressible substances, (2) operates without intentional heat transfer, and (3) has no friction internal to our system and we have the mechanical energy balance for a closed system: \[\boxed{ \frac{d}{dt} \left(E_{k}+E_{G}+E_{spring}\right)=\dot{W}_{net, \ in} } \nonumber \]
If we allow internal friction, mechanical energy can be destroyed, and it can be shown that the rate of production of mechanical energy is always less than or equal to zero. This means that internal friction always results in the destruction of mechanical energy.


