7.7: Heat Transfer Revisited
- Page ID
- 84092
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)As defined earlier, heat transfer is a mechanism for transferring energy across the boundary of a system due to a temperature difference. We further distinguish between the heat transfer \(Q\), an amount of energy (\(\mathrm{kJ}\) and \(\mathrm{Btu}\)), and the heat transfer rate \(\dot{Q}\), an energy transfer rate \((\mathrm{kW}\) and \(\mathrm{Btu} / \mathrm{s}\)). In this chapter, we will give you a very brief introduction to the subject of heat transfer. The goal is to introduce the basic mechanisms of heat transfer, not to make you an expert. Heat transfer is a mature discipline with applications in many fields. Key technologies, such as power generation or electronics and computer hardware, often face severe constraints because of limitations imposed by heat transfer processes.
7.7.1 Key concepts
There are three physical mechanisms for transferring energy by heat transfer - conduction, convection, and thermal radiation. Each of these can occur singly or in combination with the others. (Some people will argue that convection is not really a separate mechanism, but we will stick with three.)
| Name | Physical Mechanism | Examples |
|---|---|---|
| Conduction | Energy transfer within a solid, liquid, or gas due to the microscopic motion of atoms and molecules. (Diffusion) | Styrofoam cooler; thermos bottle; clothing; fiberglass wall insulation. |
| Convection | Energy transfer within a fluid due to a combination of conduction and gross fluid motion. | Heat transfer between a surface and a fluid; heating water in a pan; car radiator; |
| Thermal Radiation | Energy transfer by electromagnetic radiation | Hot sand on a beach; solar collector; thermos bottle; electric toaster. |
For use in the energy balance, we are interested in knowing the heat transfer rate; however, the heat transfer engineer often presents results in terms of the heat flux. The heat flux \(q^{\prime \prime}\) is defined as the heat transfer rate per unit area with units of \(\mathrm{W} / \mathrm{m}^{2}\) or \(\mathrm{Btu} /\left(\mathrm{h} \cdot \mathrm{ft}^{2}\right)\). The heat flux and the heat transfer rate are related by the following equation: \[\dot{Q}_{\text {surface}} = \int\limits_{A_{\text {surface}}} q^{\prime \prime} \ dA \nonumber \] When the heat flux is uniform, we have the much simpler result that the heat transfer rate equals the product of the surface area and the heat flux: \[\dot{Q}_{\text {surface}} = q^{\prime \prime} A_{\text {surface}} \quad \mid \text { Uniform heat flux } \nonumber \] This equation does not depend on the specific mechanism; however, the heat flux will change with the mechanism.
7.7.2 Conduction Heat Transfer
Conduction heat transfer occurs in solids, liquids, and gases. It is the diffusion of energy due to the microscopic motion of molecules and atoms. The diffusion process is limited by the ability of the atoms and molecules to transport the energy. The process of thermal energy diffusion is analogous to the diffusion of an ink drop placed in a glass of clear water.
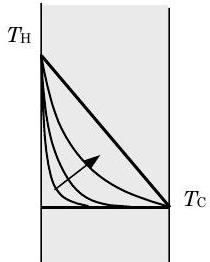
Figure \(\PageIndex{1}\): Temperature profile for transient conduction in a plane wall.
Consider the wall shown in Figure \(\PageIndex{1}\). The wall is of thickness \(L\) with a surface area \(A\) and a thermal conductivity \(k\). Initially, the wall is at a uniform temperature \(T_{\mathrm{c}}\). Suddenly the temperature of the left-hand side of the wall is changed to \(T_{\mathrm{H}}\) as shown in the figure. Once this change in the boundary temperature occurs, thermal energy starts to diffuse through the wall and causes the temperature profile to change with time. With time, as indicated by the arrow, the temperature profile reaches a steady-state distribution that is represented by the straight line from \(T_{\mathrm{H}}\) down to \(T_{\mathrm{C}}\). It takes a finite-time for the thermal energy to diffuse through the wall. At steady-state conditions, the conduction heat transfer rate through the wall is described by the equation: \[\dot{Q}_{\text {conduction}} = k \frac{A}{L} \left(T_{H}-T_{C}\right) \nonumber \] Thus the steady-state conduction heat transfer through a plane wall is proportional to the thermal conductivity, the surface area, and the temperature difference, and it is inversely proportional to the thickness of the wall. The direction of the heat transfer of energy is always from the high temperature \(T_{\text {H}}\) to the lower temperature \(T_{\mathrm{C}}\).
Conduction is a strong function of the geometry of the heat flow path, with a plane wall being one of the simplest geometries. Frequently, conduction heat transfer information is contained in something called the conduction heat transfer resistance that is defined as follows: \[R_{\text{conduction}} = \frac{\Delta T}{\dot{Q}_{\text{conduction}}} \geq 0 \nonumber \]
where all of the geometry and conductivity information is lumped into the value of the heat transfer resistance. The heat transfer resistance is always greater than or equal to zero and it typically has units of \({ }^{\circ} \mathrm{C} / \mathrm{kW}\) or \({ }^{\circ} \mathrm{F} /(\mathrm{Btu} / \mathrm{h})\). Given the heat transfer resistance and a temperature difference across the resistance, the conduction heat transfer rate is easily calculated as \[\dot{Q}_{\text {conduction}} = \frac{\Delta T}{R_{\text {conduction}}} \nonumber \] The use of a heat transfer resistance is purposely meant to draw an analogy with electrical resistance. Eq. \(\PageIndex{5}\) might be considered the "Ohm's Law" of heat transfer: the temperature difference (voltage difference) equals the product of the heat transfer rate (electric current) and the heat transfer resistance (electric resistance). This is a powerful analogy and forms the basis for problem solving in more advanced heat transfer courses.
7.7.3 Convection Heat Transfer
Convection is the transfer of thermal energy within a fluid due to a combination of conduction and gross fluid motion. More specifically we will focus on the convection heat transfer between a solid surface and an adjacent fluid as shown in Figure \(\PageIndex{2}\).
.png?revision=1)
Figure \(\PageIndex{2}\): Convection heat transfer from a surface at \(T_{\mathrm{b}}\) to a fluid at \(T_{\infty}\)
The equation used to describe the convection heat flux from the surface to the fluid is attributed to Newton and usually referred to as "Newton's Law of Cooling:" \[q^{\prime \prime}_\text { convection} = h_{\text {convection}}\left(T_{b}-T_{\infty}\right) \nonumber \] where \(T_{\mathrm{b}}\) is the surface (or boundary) temperature of the solid and \(T_{\infty}\) is the temperature of the fluid away from the surface, sometimes called the ambient temperature or the fluid temperature. The convection heat flux depends on the temperature difference and \(h_{\text {convection}}\), the convection heat transfer coefficient. The convection heat transfer coefficient is typically developed empirically and depends on the fluid properties and the motion of the fluid. Fluid motion driven entirely by the naturally occurring density differences in the fluid is called free or natural convection. Fluid motion sustained by other forces is called forced convection. On a hot day, the convection heat transfer from the leather interior of your car to the air in the car is most likely due to natural convection, while the convection heat transfer within your car's radiator is forced convection.
For conditions where the convection heat flux is uniform, the convection heat transfer rate from a surface to a fluid is described by the following equation: \[\begin{array}{l} \dot{Q}_{\text {convection}} &= h_{\text {convection}} A_{\text {surface}}\left(T_{b}-T_{\infty}\right) \\[4pt] &= \dfrac{\left(T_{b}-T_{\infty}\right)}{R_{\text {convection}}} \quad \text { where } R_{\text {convection}} = \dfrac{1}{h_{\text {convection }} A_{\text {surface}}} \end{array} \nonumber \] where we have defined a convection heat transfer resistance. This is especially useful in conjunction with the energy balance to determine the temperature of a surface exposed to a fluid. If you can use the energy balance to solve for the heat transfer rate at the system boundary and you know the heat transfer resistance and the ambient fluid temperature, you can calculate the surface temperature at the boundary. In this course, when necessary we will give you the appropriate heat transfer coefficient values; however, in practice, determining the correct values for any given situation is one of the major challenges for a heat transfer engineer.
7.7.4 Thermal Radiation Heat Transfer
Last but not least, we come to thermal radiation heat transfer. We add the modifier "thermal" to distinguish this from nuclear radiation. Thermal radiation is the transfer of thermal energy between surfaces at different temperatures by electromagnetic radiation. It is the only heat transfer mechanism that can occur across a vacuum.
We will only consider one specialized case-thermal radiation heat transfer between a small convex object and its surroundings (See Figure \(\PageIndex{3}\)). Because this is a specialized case, we must be careful to explain the geometric limitations. By "small" we mean an object with a surface area much, much smaller than the surroundings it sees. By "convex body" we mean an object that cannot see itself. A baseball (or any sphere for that matter) is a convex surface; however, a baseball glove is not. The outer surface of a cylinder is a convex surface. The outside surface of a foam coffee cup is a convex surface. Thermal radiation proceeds between surfaces just like visible light. A convex surface is one where a person standing on the surface (a very small person) can scan the sky from horizon to horizon and not see the surface they are standing on.
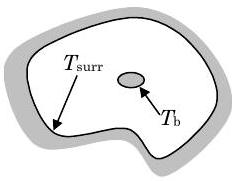
Figure \(\PageIndex{3}\): Thermal radiation between a small convex object and its surroundings.
The thermal radiation heat transfer rate between a small convex object at temperature \(T_{\mathrm{b}}\) and the surroundings at temperature \(T_{\mathrm{surr}}\) is given by the equation: \[ \begin{align} \quad\quad\quad\quad\quad\quad\quad& \dot{Q}_{\text {radiation}} = A_{\text {surface}}\left[\varepsilon \sigma\left(T_{b}^{4}-T_{\text {surr}}^{4}\right)\right] \\ \text{where }& \nonumber \\ &\sigma = \text {Stefan-Boltzmann constant } \left\{\begin{array}{c} =5.669 \times 10^{-8} \mathrm{~W} /\left(\mathrm{m}^{2} \cdot K^{4}\right) \\ =0.1714 \times 10^{-8} \mathrm{Btu} /\left(\mathrm{hr} \cdot \mathrm{ft}^{2} \cdot{ }^{\circ} \mathrm{R}^{4}\right) \end{array}\right. \nonumber \\ &\varepsilon = \text {emissivity of the surface of the convex body} \leq 1 \nonumber \\ & A_{\text {surface}} = \text {surface area of the convex body} \nonumber \\ & T_{b} =\text {surface temperature of the convex body }\left(\text {in } \mathrm{K} \text { or }^{\circ} \mathrm{R}\right) \nonumber \\ & T_{\text {surr}} = \text {temperature of the surroundings (in } \mathrm{K} \text { or }^{\circ} \mathrm{R} \text {)} \nonumber \end{align} \nonumber \]
You should note that this equation has some significant differences from the previous two heat transfer rate equations we have discussed. First, note that the heat transfer rate is proportional to the difference between the absolute temperature of the body raised to the fourth power and the absolute temperature of the surroundings raised to the fourth power. Radiation heat transfer is not proportional to the simple temperature difference we saw with convection and conduction.
Second, the radiation heat transfer rate is directly proportional to the condition of the surface as indicated by the value of the emissivity of the surface. Emissivity values range from \(0\) to \(1\). The shinier the surface, the lower the emissivity value. A sheet of polished metal will typically have emissivity values on the order of \(0.05\), whereas oxidized metals will have values greater than \(0.5\). Red building brick with a rough surface has an emissivity in the range of \(0.9\). Radiation heat transfer depends strongly on the surface characteristics and finding an accurate emissivity value for a specific situation is a significant challenge.
Third, the temperature of the surroundings is not necessarily the temperature of the fluid adjacent to the object, but it is the temperature of the surrounding surfaces that the object sees. In our special case, we are assuming that the material in the void between the object and the surroundings does not participate in the heat transfer process. This is not always true. In many cases, the radiation proceeds from the surface of the object to the participating media in the void and finally to the surroundings.
Finally, we have totally ignored the wavelength dependence of thermal radiation. This is the phenomenon that causes a greenhouse to heat up. Solar radiation with one wavelength distribution passes easily through a glass window, while thermal radiation emitted from surfaces near room temperature with a significantly different wavelength distribution cannot pass back through the window and is trapped inside the greenhouse.
The last point to make about thermal radiation heat transfer is that it can occur in parallel with both of the other mechanisms we have discussed. Our main interest in this course will be cases where convection and thermal radiation occur in parallel from a surface. Under these conditions, the heat transfer rate from the surface is found by adding the contributions of convection and thermal radiation as follows:
\[\begin{array}{l} \dot{Q}_{\text {surface}} &= \dot{Q}_{\text {convection}}+\dot{Q}_{\text {radiation}} \\ &= h_{\text {convection }} A_{\text {surface}}\left(T_{b}-T_{\infty}\right) + A_{\text {surface}}\left[\varepsilon \sigma\left(T_{b}{ }^{4}-T_{\text {surr}}{ }^{4}\right)\right] \end{array} \nonumber \] Note that there are three temperatures in this formulation: the temperature of the boundary of the object \(T_{b}\), the temperature of the fluid adjacent to the body \(T_{\infty}\), and the temperature of the surrounding that an object sees \(T_{\text {surr}}\). Each of these may be different. Often the fluid and surroundings temperatures are assumed to be equal if surroundings temperature does not differ significantly from the fluid temperature.
This problem is for those of you who have sat in a warm room on a cold day and felt chilled.
Assume that we know you are comfortable when you sit in a room where the air temperature and the temperature of the surrounding walls are both \(20^{\circ} \mathrm{C}\) \((293 \mathrm{~K})\). Under these conditions, your skin temperature is \(25^{\circ} \mathrm{C}\) \((298 \mathrm{~K})\). Assume that the surface area of your arm is \(0.120 \mathrm{~m}^{2}\), that your skin has an emissivity of \(0.8\), and that the heat transfer coefficient from your skin is \(10 \mathrm{~W} /\left(\mathrm{m}^{2}\cdot^{\circ} \mathrm{C}\right)\) and your skin loses no energy by heat transfer.
(1) Calculate the combined heat transfer rate from your arm by radiation and convection. This energy must be supplied to your skin by the blood supply to your arm. [Hint: Use Eq. \(\PageIndex{9}\). Remember to use absolute temperatures \((K)\) in your calculations.] What percentage of the heat transfer is by convection and by radiation?
(2) Now you are sitting in a room where the walls (the surroundings) are at \(5^{\circ} \mathrm{C}(278 \mathrm{~K})\) because of faulty insulation in the walls. Because of the heating system, the air temperature is the same as before. Assuming the heat transfer rate to your skin that you calculated in (1) remains the same when you move to the new room, what is the temperature of your skin in the new conditions. Does it increase or decrease or stay the same? Does this explain why you feel chilled? [Hint: This may require an iterative solution since \(T_{\mathrm{b}}\) appears in two places.]
It is very common to neglect thermal radiation heat transfer; however, when the convection heat transfer coefficient is low or the temperature difference is large, thermal radiation can be very important

