12.7: The Lever Rule
- Page ID
- 36301
If an alloy consists of more than one phase, the amount of each phase present can be found by applying the lever rule to the phase diagram.
The lever rule can be explained by considering a simple balance. The composition of the alloy is represented by the fulcrum, and the compositions of the two phases by the ends of a bar. The proportions of the phases present are determined by the weights needed to balance the system.

So,
fraction of phase 1 = (C2 - C) / (C2 - C1)
and,
fraction of phase 2 = (C - C1) / (C2 - C1).
Lever rule applied to a binary system
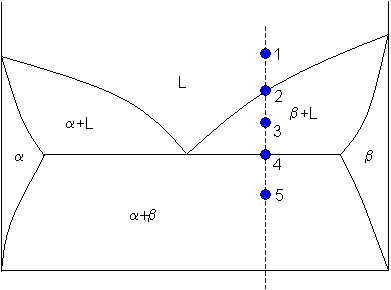
Point 1
At point 1 the alloy is completely liquid, with a composition C. Let
C = 65 weight% B.
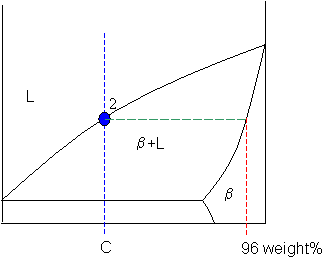
Point 2
At point 2 the alloy has cooled as far as the liquidus, and solid phase β starts to form. Phase β first forms with a composition of 96 weight% B. The green dashed line below is an example of a tie-line. A tie-line is a horizontal (i.e., constant-temperature) line through the chosen point, which intersects the phase boundary lines on either side.
Point 3
A tie-line is drawn through the point, and the lever rule is applied to identify the proportions of phases present.
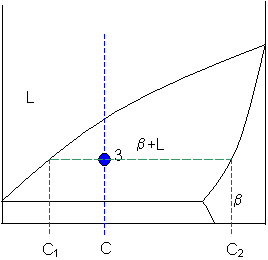
Intersection of the lines gives compositions C1 and C2 as shown.
Let
C1 = 58 weight% B
and
C2 = 92 weight% B
So,
fraction of solid β = (65 - 58) / (92 - 58) = 20 weight%
and
fraction of liquid = (92 - 65) / (92 - 58) = 80 weight%
Point 4
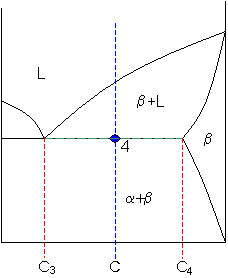
Let
C3 = 48 weight% B
and
C4 = 87 weight% B
So
fraction of solid β = (65 - 48) / (87 - 48) = 44 weight%.
As the alloy is cooled, more solid β phase forms.
At point 4, the remainder of the liquid becomes a eutectic phase of α+β and
fraction of eutectic = 56 weight%
Point 5
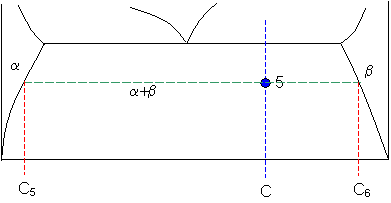
Let
C5 = 9 weight% B
and
C6 = 91 weight% B
So
fraction of solid β = (65 - 9) / (91 - 9) = 68 weight%
and
fraction of solid α = (91 - 65) / (91 - 9) = 32 weight%.


