4.1: Introduction
- Page ID
- 8185
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Nuclear Processes
Each nucleus, consisting of protons and neutrons (collectively known as nucleons), has an associated binding energy. A graph of binding energy per nucleon is shown in the graph below. The total binding energy of a nucleus is the energy released when a nucleus is assembled from individual nucleons; the greater the energy release, the lower the potential energy of the nucleus, so higher binding energy in the graph represents greater stability. When one nucleus is converted to another or others of higher binding energy, whether that be through a natural radioactive process or through an artificially induced process, the difference in the total binding energies of the nuclei is released as kinetic energy of the particles produced and gamma rays. This energy can be harnessed through traditional methods, e.g. by heating water to generate steam to drive a turbine, and so electricity can be produced.
Origins of Binding Energy
The measured binding energies of the nuclides can be fitted reasonably well by Weizsäcker’s formula (see below). The formula is derived by treating the nucleus as analogous to a liquid drop, with surface energy and volume energy terms leading to the two dominant contributions: a term proportional to A, the atomic mass and to the volume of the nucleus, and a term proportional to -A2/3 due to the surface energy. These two terms compete, much in the same way they do in other processes (e.g. nucleation), facilitating a qualitative understanding of why nuclei split up or join together under certain conditions.
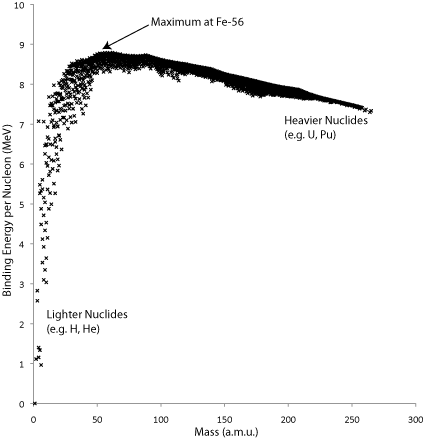
A graph of the binding energy per nucleon, in MeV, for common nuclides.
Fusion
Energy is given off when a nucleus becomes more stable, i.e. approaches the maximum on the graph above. Moving from lighter nuclei towards this maximum requires two nuclei to combine and form a heavier one (fusion), whereas moving from heavier nuclei towards this maximum requires the nucleus to split apart (fission). The energy release per mass of nuclide is much higher for fusion than for fission. Fusion has many other attractive attributes as a basis for power generation, but since nuclei are positively charged, sufficient energy most be put into the system to overcome the repulsion between nuclei so that a fusion process can occur. This Coulomb barrier can also be expressed as an ignition temperature. The technical challenges are many, and nothing close to a commercially viable reactor currently exists. Fusion for power generation is still a prominent research topic, and experimental reactors are in the process of being built, such as ITER (International Thermonuclear Experimental Reactor), which is planned to be completed by 2018.
Since nuclear fusion is not yet a practical power source, this TLP will instead focus on nuclear fission as means to generate heat and electricity.
Fission
Nuclear fission, as previously mentioned, involves splitting a heavier nucleus into two lighter nuclei. Fission can be induced if a nucleus absorbs a neutron of sufficient energy. If a nucleus undergoes fission regardless of the incident neutron energy, the nucleus is referred to as fissile; otherwise, if there is a threshold energy then the nucleus is referred to as fissionable.
Examples of fissile nuclides include 233U, 235U and 239Pu. The nuclide most commonly used in nuclear reactors is 235U.
A neutron will not necessarily induce fission if it passes through the nucleus. For example, fast neutrons are less likely to induce fission in 235U than thermal neutrons (i.e. neutrons with kinetic energy of the order of kT). Qualitatively, this makes sense since the faster a neutron is travelling the less time it spends inside the nucleus and so the less opportunity it has to induce fission within the nucleus. The actual reasons for this are complicated, and this topic is explored further on the “Cross Sections” page.
Fissionable nuclides, such as 238U and 239Pu, are also used in so-called “fast” reactors, where the neutrons are travelling fast enough (commonly around 10% the speed of light, or 1 MeV) to overcome the activation energy required to make fissionable nuclides decay.
The movie below illustrates the fission process:
https://www.doitpoms.ac.uk/tlplib/nu...lustration.mp4
Video illustrating nuclear fission
As can be seen in the movie, the parent nucleus decays into two fission fragments of unequal mass with a combined kinetic energy of about 169 MeV and several neutrons with a kinetic energy of about 2 MeV each (for 235U, the average number of neutrons produced is 2.4, but can be as high as 5). These neutrons are highly energetic, with 7–8 orders of magnitude more energy than thermalized neutrons. A gamma ray of about 7 MeV is also released. The neutrons could induce further fission events in other nuclei and thus cause a chain reaction, but in practice they are too fast and must first be slowed down inside the reactor.
![This graph shows that fragments formed tend to be of unequal masses, with each fragment being Gaussian distributed about a particular lower/higher mass respectively. Graph is under a CC[BY][NC][SA] license graph and was created from source data at http://www-nds.iaea.org/sgnucdat/c1.htm This graph shows that fragments formed tend to be of unequal masses, with each fragment being Gaussian distributed about a particular lower/higher mass respectively. Graph is under a CC[BY][NC][SA] license graph and was created from source data at http://www-nds.iaea.org/sgnucdat/c1.htm](https://www.doitpoms.ac.uk/tlplib/nuclear_materials/images/fission-products-graph.png)
Graph showing the distribution of fission fragment mass numbers for three nuclides, U-233, U-235 and Pu-239.
The fragments formed tend to be of unequal masses, with each fragment showing a Gaussian distribution about a particular lower or higher mass. [Graph is under a CC[BY][NC][SA] licence and was created from source data at www-nds.iaea.org/sgnucdat/c1.htm]
The nuclides produced by fission are usually of unequal mass, as shown in the graph above. The x-axis of the graph is by atomic mass, not atomic number. Many fission fragments are highly unstable, and decay by giving off beta radiation: this involves a neutron changing into a proton within the nucleus, leaving the overall number of nucleons (and hence the mass of the nucleus) the same.
Nuclear Power Generation
There are two main types of nuclear reactor, characterized by the speed of the neutrons which induce fission:
- Thermal reactors. These are the predominant kind, using slower neutrons to induce fission, the basic fissile nuclide being U-235.
- Fast breeder reactors. In these less-common reactors, the fast neutrons are used directly to create (breed) fissile nuclides from fissionable nuclides; most commonly Pu-239 is bred from U-238. Pu-239 is also used in nuclear weapons.
There are many varieties of nuclear reactor, but all have the following common elements:
Fuel: The material that undergoes fission. This needn’t have the fissionable nuclides in the form of the element. The fuel is often in the form of a ceramic.
Cladding: This encases the nuclear fuel, isolating it mechanically and chemically from its immediate environment.
Moderator: Necessary in thermal reactors to slow down the neutrons produced by the fission process. Commonly, the moderator is in the form of a rod, but can be in liquid form or even be mixed with the fuel itself.
Control: This can be used to absorb excess neutrons, or even shut down the reactor in an emergency. Most often, the control material is in the form of a rod.
Core: The heart of the reactor, containing the fuel. The fuel is encased in cladding, and core must also accommodate the coolant and allow for more moderating rods or control rods to be added.
Coolant: The coolant removes heat from the reactor core into a heat exchanger. Note that the coolant itself is not cool, just that it removes heat from the core.
Reactor vessel: This contains the reactor core and the coolant. It often also acts as a reflector, reducing the loss of neutrons to the outside environment.
Generator/turbine: The heat generated by the reactor core generates steam, used to drive a turbine, which can generate electricity.
The following simulation demonstrates these main components in use.
The types of reactor are loosely grouped into generations describing the time period in which they were first used. Advances in technology have led to new designs.
The current generation of reactors can be defined by the materials used for each of these components. They include Pressurised Water Reactors (PWR), the most common reactor type, Boiling Water Reactors (BWR), CANDU or Pressurised Heavy Water Reactor (PHWR). These all include water as a coolant in some form. There are also Gas Cooled Reactors (GCR) and Advanced Gas Cooled Reactors (AGR), which use CO2 as coolant. Finally, there are also Liquid Metal Fast Breeder Reactors (LMFBR), which are cooled by a liquid metal (sodium or lead). There are also many other forms of reactors used for research purposes.
The next generation, commonly referred to as Generation IV, in some cases are just incremental improvements on these designs, but in other cases are radically different designs aimed at increasing efficiencies and reducing risk. The latter may demand materials which can sustain exposure to much more extreme environments.


