4.3: Mechanisms of Radiation Damage
- Page ID
- 8187
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Most of the radiation damage in a reactor is from the neutron flux being produced in the core. Other forms of radiation, such as gamma radiation, are very weakly interacting and don’t produce much effect. The principles in this section can in theory apply to any material, but the key materials are steels (e.g. a cold-worked 316 stainless steel).
Transmutation – (n, α) – Production of Helium
As seen in the previous section, there are several ways in which neutrons can interact with nuclei, including absorption of the neutron by the nucleus, making the nucleus unstable so that it decays, releasing an alpha particle in the process. Alpha particles consist of two protons and two neutrons, i.e. a 4He nucleus. Since they are 2+ positively charged, they are very highly ionizing, and will they quickly pick up electrons from the surrounding lattice and become elemental helium.
In stainless steels, the (n, α) interaction does not occur often with iron itself, but is mostly as a result of the nickel content of the alloy, as the graph of its cross section below shows.
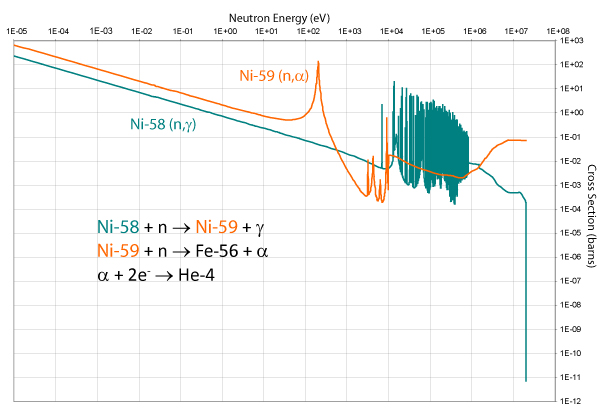
The presence of helium in the metal causes embrittlement and can act as a nucleation point for voids, which can lead to swelling.
Additionally, the neutron flux can induce further radiation. This occurs when a neutron transmutes an element into a radioactive one. This is undesirable, because it creates more low-level radioactive waste to contain when the reactor is eventually decommissioned.
Frenkel Defects
There are many proposed mechanisms of radiation damage, but on a fundamental level a single neutron scattering event can be considered.
If a neutron of sufficient energy scatters off a nucleus, the nucleus itself is displaced. The atom associated with the nucleus finds itself embedded into the structure elsewhere in a high-energy, interstitial site. It is termed a self-interstitial as the matrix and interstitial atoms are in principle the same. The site the atom previously occupied is now empty: it is a vacancy. In this way, self interstitial-vacancy pairs are formed, and these are called Frenkel defects.
Threshold Energy
At lower energies, the neutron collision causes the nucleus to vibrate, but the nucleus is not displaced. The excess energy is dissipated through the lattice as heat. The threshold energy to form a Frenkel defect depends on the nuclei present and the structure of the material (e.g. the phase of iron). It is typically in the range 10–50 eV (2–8 × 10−18 J). Note that when the neutron scatters off a nucleus, not all of its energy is transferred. This means that the minimum kinetic energy of the neutron is be larger than this threshold value, typically by a factor of 2–3.
This threshold energy is commonly given the symbol Ed. It is the energy required to overcome the potential barrier to move from one lattice site to another, and is approximately twice Es, the energy of sublimation, since twice as many bonds are broken to move an atom within a lattice as removing it from its surface, plus a contribution of 4–5 Ec, where Ecis the energy loss by electron stopping (required to allow the lattice to relax after the atom has been displaced).
Displacement Spikes
Neutron scattering events are not isolated. On average, each displaced atom might then go on to displace further atoms, and likewise the neutron that caused the first displacement might go on to displace further atoms. This means that there is a local cascade of displacements, known as a displacement spike, within which there is a large amount of disorder in the structure. This is illustrated with a simulation, below:
The Kinchin and Pease Model
A neutron scattering from an atom imparts an energy Ep to it. This primary knock-on atom (PKA) with energy Ep then displaces other atoms, ultimately giving a displacement cascade if Ep is high enough. The number of atoms displaced by the PKA is difficult to calculate, but a simple model (attributed to Kinchin and Pease) can capture much of the basic physics. The assumptions are:
- the cascade is a sequence of two-body elastic hard-sphere collisions;
- a minimum energy transfer Ed is required for displacement;
- the maximum neutron energy available for transfer is the cut-off energy Ec, set by loss to the electrons (electron stopping);
- the atoms are randomly distributed, so that channelling and other effects of crystal structure are ignored.
A full derivation can be found in Fundamentals of Radiation Science by Gary Was. The average number of atoms displaced by a PKA of energy Ep is:
0 for Ep< Ed
1 forEd < Ep< 2Ed
Ep/2Ed for 2Ed < Ep<Ec
Ec/2Ed for Ep ≥Ec
Formation of Dislocation Loops
Both the interstitial atoms and vacancies can diffuse through the lattice, but the interstitial atoms are more mobile. Both interstitials and vacancies are eventually removed from the lattice (when they reach sinks such as dislocations or grain boundaries). However, they are also always being generated by the neutron radiation. Thus steady-state populations of interstitials and vacancies are formed.
There is a tendency for interstitial atoms and vacancies respectively to aggregate together into discs. This is again illustrated through an animation, below:
Note: This animation requires Adobe Flash Player 8 and later, which can be downloaded here.
When there is a sufficient supersaturation of vacancies, the disc of vacancies grows and the gap between the planes on either side collapses to form a continuous lattice with a dislocation loop. Since the Burgers vector is normal to the plane loop, it is an edge dislocation and grows/shrinks by climb and moves by glide along a prism; it is termed a prismatic loop.
Nucleation and Growth of Voids
Vacancy dislocation loops should reduce the volume of the material whilst interstitial dislocation loops should increase it, as seen in the animation above. And, in general, we expect compensating vacancy and interstitial effects to leave the material with approximately the same volume. However, irradiated materials are in fact observed to swell.
To explain this, we consider what happens when vacancy loops join together. In practice, when the loops join they form three dimensional cavities a few nm in diameter. These voids contribute no net change in volume to the material, and so this just leaves the interstitial loops, which do lead to swelling in the material.
In the absence of any driving force, it would seem unlikely that enough voids would form for any appreciable effect to be observed on the material. This is where the transmutation of nickel becomes important, since the helium atoms produced are very small and are thus extremely mobile as interstitial atoms in the lattice. They quickly form bubbles, and these helium bubbles can act as nucleation points for void formation.


