9.2: Background
- Page ID
- 8221
Electrode potentials
The electrode potential, E, of a metal refers to the potential difference measured (in volts) between a metal electrode and a reference electrode.
Ee is the equilibrium potential (or reversible potential), which describes the equilibrium between two different oxidation states of the same element, at whatever concentration (or pressure) they occur. Ee varies with concentration, pressure and temperature. It describes the electrode potential when the components of the reaction are in equilibrium. This does NOT mean that they are in equilibrium with the standard hydrogen electrode. It means only that the reaction components are in equilibrium with each other. In the reaction
Az+ + ze- = A,
a concentration, CAz+, of AZ+ is in equilibrium with solid A. The reaction moves away from equilibrium only if there is a source or sink for electrons. If this were the case, then the potential would move away from Ee.
E0, the standard equilibrium potential (or standard electrode potential), is defined as the equilibrium potential of an electrode reaction when all components are in their standard states, measured against the standard hydrogen electrode (SHE). It describes the equilibrium between two different oxidation states of the same element. E0 is a constant for a given reaction, defined at 298 K. Values of E0 for various electrochemical reactions can be found in data books.
At equilibrium, the chemical driving force for an electrochemical reaction, ΔG is equal to the electrical driving force, Ee. ΔG corresponds to a charge, zE, taken through the potential, Ee. The measured potential for an electrochemical reaction is therefore directly proportional to its free energy change.
ΔG = -zE Ee
where z is the number of moles of electrons exchanged in the reaction and E is Faraday’s constant, 96 485 coulombs per mole of electrons. Similarly, under standard conditions,
ΔG0 = -zE E0
Aqueous corrosion
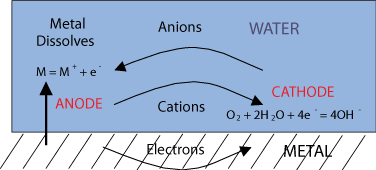
Oxidation of a metal in an aqueous environment is dependent on potential,E, and pH.
If oxidation does occur, the metal species is oxidised and loses electrons, forming metal cations; and a corresponding reduction reaction that consumes electrons at the cathode
In aqueous corrosion water is the electrolyte, an ion-conducting medium. This means that the sites of oxidation and reduction can be spatially separate. This is different from a gaseous environment, as a gas cannot conduct ions.
A metal oxidising to produce metal ions may dissolve into the water, resulting in corrosion. This is different from corrosion in a gas, where the oxidised metal stays where it is produced, as an oxide film on the metal.
Electrochemical half-cell reactions
A half-cell reaction is an electrochemical reaction that results in a net surplus or deficit of electrons. It is the smallest complete reaction step from one species to another. Although this reaction may proceed as a sequence of more simple reactions, these intermediate stages are not stable.
A half-cell reaction can either be a reduction, where electrons are gained, or an oxidation, where electrons are lost.
The following mnemonic is often helpful:
OILRIG: Oxidation Is Loss; Reduction Is Gain (of electrons).
The anode is the site of oxidation –where electrons are lost.
The cathode is the site of reduction –where electrons are gained.
Anions, such as O2-, are negatively charged ions, attracted to the anode.
Cations, such as Fe2+, are positively charged ions, attracted to the cathode.
Reduction half-cell reactions
Reduction reactions occur at the cathode and involve the consumption of electrons. In corrosion these normally correspond to reduction of oxygen or evolution of hydrogen, such as:
O2 + H2O + 4e- = 4OH-
O2 + 4H+ + 4e- = 2H2O
2H2O + 2e- = H2 +2OH-
2H+ + 2e- = H2
Oxidation half-cell reactions
Oxidation reactions occur at the anode and involve the production of electrons. For the corrosion of metals, these reactions normally correspond to the various metal dissolution or oxide formation reactions, such as:
Fe = Fe2+ + 2e-
Fe2+ = Fe3+ + e-
Fe + 2OH- = Fe(OH)2 + 2e-
2Fe + 3H2O = Fe2O3 + 6H+ + 6e-
In addition to causing corrosion, oxidation may result in the formation of a passive oxide. The passive oxide produced may protect the metal beneath from further corrosion –significantly slowing further corrosion. An example of such passivation is that of aluminium in water, where aluminium is oxidised to from a layer of Al2O3 that protects the metal beneath from further oxidation.
Reference electrodes
Since only differences in potential can be measured, a benchmark electrode is required, against which all other electrode potentials can be compared. The particular reference electrode used must be stated as part of the units.
The Standard Hydrogen Electrode (SHE)
The electrode reaction
2H+ + 2e- = H2
is defined as having an electrode potential, EH+/H2 of zero volts, when all reactants and products are in the standard state. The standard chemical potential of H+ at 1 molar (M) concentration is by definition equal to zero.
The standard state is defined as 298 K, 1 bar pressure for gases and a concentration 1 molar (1 mol dm-3) for ions in aqueous solution.
As a direct result of this, the standard hydrogen electrode (SHE) is commonly used as a reference electrode. When coupled with an electrode, the potential difference measured is the electrode potential of that electrode, as the SHE establishes by definition the zero point on the electrochemical scale.
The standard hydrogen electrode consists of a platinum electrode suspended in a sulphuric acid solution with a one molar concentration of H+. Purified hydrogen is bubbled through to equilibrate the 2H+ + 2e- = H2 electrode reaction.
[Pop-up for other reference electrodes]
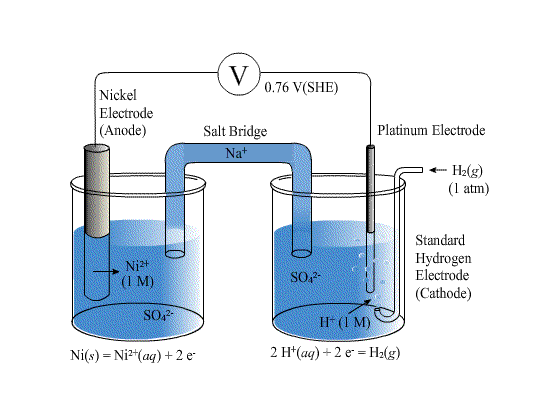
The diagram above shows how the standard potential,E0 of nickel can be determined. The nickel electrode contains Ni2+ ions in equilibrium with nickel metal.
The hydrogen electrode is linked via a salt bridge to the deaerated solution in which the nickel electrode is immersed. This permits charge transfer and potential measurement but not mass transfer of the acid solution in the electrode.
When Ee or E0 are measured relative to the SHE (or some other reference electrode), a voltmeter is used. The voltmeter is required to have a high impedance to resist any current flowing between the electrode and the SHE. If a current were allowed to flow, the electrodes would become polarised and would no longer be at equilibrium.
In practice, it is often difficult or impossible to determine experimentally the standard electrode potential for electrochemical systems. Many systems lie outside the water stability zone or are passive. For example, zinc will immediately begin to oxidise when immersed in water.
It is very simple to determine accurately the standard equilibrium potential from the equation linking chemical driving force with the electrical driving force,
ΔG0 = -zF E0
Now ΔG0, the standard free energy of formation can be expressed as
ΔG0 = μ0(products) − μ0(reactants)
where μ0 is the standard chemical potential. By combining these equations,
\[E^0 = \frac{\Delta G^0}{zF} = \frac{\mu^0(products) - \mu^0(reactants)}{zF} \]
To obtain a standard equilibrium potential, E0, for an electrochemical reaction, all that is required is to look up relevant values of standard chemical potential.
How corrosion of metal occurs
If a metal surface is immersed in an electrolyte such as water, metal ions tend to be lost from the metal into the electrolyte, leaving electrons behind on the metal. This will continue to occur until the metal reaches its equilibrium potential and the system comes to equilibrium, with a certain concentration of dissolved ions. The metal is at its equilibrium potential, Ee. If the electrolyte were to be continuously replaced (by water flowing in through a pipe for example), more and more metal ions would be lost, resulting in continuous corrosion of the metal.
A cathodic reaction may occur that uses up the electrons lost by the metal species. In the reaction,
2H+ + 2e- = H2
if the hydrogen gas evolved is lost from the system, the reaction is prevented from reaching equilibrium.
The cathodic reaction acts as a sink for electrons liberated in the oxidation reaction of the metal. As a result of this, the metal will not reach its equilibrium potential. The metal oxidation reaction is therefore not in equilibrium and carries a net reaction. The difference between the potential, E, of the metal and its equilibrium potential, Ee is called the overpotential and is given the symbol η.
η = E − Ee
As corrosion occurs, the mass of metal is reduced due to the conversion of atoms to ions, which are subsequently lost. The sites of oxidation (the anode) and reduction (the cathode) can both be situated on the same piece of metal – there is no need for an external electrode to be present for the process to occur.
Rules for balancing electrochemical equations
The aim of this procedure is to balance electrochemical equations in terms of electronic charge and moles of components, given the main reaction product and reactant.
By convention, electrochemical reactions are written as the REDUCTION of the species concerned, proceeding to the right. The species with the lower oxidation state is written on the right hand side.
The rules are as follows:
1. Write down the main reaction components, with the reduced form (the form with the lowest valency) on the right.
2. Add stoichiometric numbers to balance the number of metal atoms. (Don’t worry about charge or oxygen being balanced at this point).
3. Balance the number of oxygen atoms by adding H2O to the appropriate side.
4. Balance the number of hydrogen atoms by adding hydrogen ions (H+) to the appropriate side.
5. Balance the residual charge by adding electrons (e-) to the appropriate side.
Now each side of the equation has the same number of atoms of each element and the same overall charge.
Examples of balancing electrochemical reactions
Find the electrochemical reaction for an equilibrium between Cr2O3 and CrO42-
1. Write reduced species on right
CrO 42- → Cr2O3
2. Balance Cr metal atoms
2 CrO 42- → Cr2O3
3. Balance oxygen atoms with water
2 CrO 42- → Cr2O3 + 5 H2O
4. Balance hydrogen atoms with hydrogen ions
2 CrO 42- + 10 H+ → Cr2O3 + 5 H2O
5. Balance charge with electrons
2 CrO 42- + 10 H+ + 6 e- → Cr2O3 + 5 H2O
Check: Each side of the equation has: Two Cr, eight O, ten H and zero residual charge – so it is balanced.
Click for more examples:
Example \(\PageIndex{1}\)
Find the electrochemical reaction for an equilibrium between Zn and Zn(OH)42–
1. Write reduced species on right
Zn(OH) 4 2– → Zn
2. Balance zinc atoms
Zn(OH) 4 2– → Zn
3. Balance oxygen atoms with water
Zn(OH) 4 2– → Zn + 4 H2O
4. Balance hydrogen atoms with hydrogen ions
Zn(OH) 4 2– + 4 H+ → Zn + 4 H2O
5. Balance charge with electrons
Zn(OH) 4 2– + 4 H+ + 2 e- → Zn + 4 H2O
Check: Each side of the equation has: One Zn, four O, four H and zero residual charge – so it is balanced.
Example \(\PageIndex{1}\)
Find the electrochemical reaction for an equilibrium between NO3- and NO.
1. Write reduced species on right
NO3- → NO
2. Balance nitrogen atoms
NO3- → NO
3. Balance oxygen atoms with water
NO3- → NO + 2 H2O
4. Balance hydrogen atoms with hydrogen ions
NO3- + 4 H
5. Balance charge with electrons
NO3- + 4 H + + 3e- → NO + 2 H2O
Check: Each side of the equation has: One N, three O, four H and zero residual charge – so it is balanced.
Example \(\PageIndex{1}\)
Find the electrochemical reaction for an equilibrium between MnO4- and MnO2
1. Write reduced species on right
MnO4- → MnO2
2. Balance Mn atoms
MnO4- → MnO2
3. Balance oxygen atoms with water
MnO4- → MnO2 + 2H2O
4. Balance hydrogen atoms with hydrogen ions
MnO4- + 4 H+ → MnO2 + 2H2O
5. Balance charge with electrons
MnO4- + 4 H+ + 3 e- → MnO2 + 2H2O
Check: Each side of the equation has: One Mn, four O, four H and zero residual charge – so it is balanced.


