6.5: Thermal Energy

Temperature and heat are important phenomena that start to unlock the ideas of thermodynamics. Temperature is something that impacts our lives greatly as we move throughout the seasons. Heat and specific heat capacity are concepts that allow us to understand climate and cooling systems, among other things. Finally, thermal expansion has far-ranging implications from the existence of aquatic life on this planet, to understanding how objects change their sizes from month to month as temperatures change.

Temperature

Temperature quantitatively describes the average translational kinetic energy of the atoms and molecules in a substance. It quantifies the “hotness” or “coldness” of something. The symbol for temperature is the uppercase letter \(T\).

Kinetic energy describes the energy of motion. Therefore, it would be reasonable to expect that a substance at a higher temperature will have more motion than a substance at a lower temperature.

In the video below, there are two beakers filled with water. The beaker on the left is filled with cold water, and the beaker on the right is filled with hot water. (The beaker on the left appears translucent due to the fact that water vapor from the air has condensed on it.)

A drop of blue food dye is dropped into each beaker. After watching for several moments, you can see the food dye swirl around and distribute itself much more rapidly in the beaker of hot water, demonstrating that its motion is much greater than that of the cold water. A photograph of each beaker 30 seconds after the introduction of the food dye is shown in Figure \(\PageIndex{1}\). The dye in the cold beaker (left) has not distributed nearly as much as the dye in the hot beaker (right).

Figure \(\PageIndex{1}\) – A beaker of cold water (left) and hot water (right) are viewed 30 seconds after placing a drop of blue food coloring in each beaker. The dye in the hot water has distributed much more than the dye in the cold water. This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0. 

From a human perspective, temperature is extremely important in helping us determine what to wear when we go outside, and in deciding on what types of indoor and outdoor activities we want to do. Having an objective temperature scale is important in that it cuts out the subjective interpretation of each person’s idea of what may be “hot” or “cold.” From a physics perspective, an objective temperature scale enables scientists to perform experiments on thermodynamics, climate change, and other important phenomena.

Empirical temperature scales

Now that we understand what temperature is, we need a way to measure it. There are two types of temperature scales that can be used: empirical scales and absolute scales.

An empirical scale means that experiments were performed to derive the upper and lower limits of the scale. The Fahrenheit scale was proposed in the 1700s. The limit for the cold end of the temperature scale was a frozen salt water solution. That temperature was denoted as zero. The limit for the hot end of the temperature scale was the temperature of a human body. This temperature was denoted at 96. (This value was chosen because it is easily divisible by many numbers; it has 12 divisors.) The total number of degrees on this scale was therefore 96, creating the original Fahrenheit temperature scale. This rudimentary scale is shown in Figure \(\PageIndex{2}\) .

 

Figure \(\PageIndex{2}\) – The original Fahrenheit scale was developed by setting 0 as the temperature of a frozen salt water solution and setting 96 as the temperature of the human body. This created a total number of 96 degrees between hot and cold. This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

The basis of the Fahrenheit scale isn’t terribly scientific because it’s not repeatable. Depending on how much salt is placed in the freezing salt water solution, and whether or not the person whose body temperature is measured is sick with a fever, there will be different definitions of 0 and 96 Fahrenheit. Even if we standardize how much salt to place in the water, we are still limited by the variations in human body temperature.

Since the development of the Fahrenheit scale, it has been standardized such that temperature measurements using this scale are now repeatable and scientific. This allows meteorologists (and others) in the United States (one of the only countries in the world that continues to use this scale) to record temperatures in degrees Fahrenheit that are comparable from day to day and over time. While the Fahrenheit scale is admittedly useful as a temperature scale, as we tend to experience the full range of temperatures from zero to one hundred (particularly in varied climates), it was not created with a scientifically sound basis.

The Celsius scale was also developed in the 1700s. The cold end of the temperature scale is established by the freezing point of water at 1 atmosphere of pressure, and is called zero Celsius. (A photograph of a Celsius thermometer reading zero degrees in a bath of ice water is shown in Figure \(\PageIndex{3}\).) The hot end of the temperature scale is established by the boiling point of water at 1 atm of pressure, and is called one hundred Celsius. This means that there are 100 degrees between the cold and hot ends of the Celsius scale. (Note that the original Celsius scale was actually inverted such that 0 degrees indicated the boiling point of water, and 100 degrees indicated the freezing point of water.)

Figure \(\PageIndex{3}\) – A Celsius thermometer reads zero degrees as it is submerged in a container of ice water. Melting ice thermometer, by Ulflund, is licensed under CC0.

The selection of the cold and hot ends of the thermometer establishes the temperature scale and allows us to measure temperatures in between those two extremes. (We can also extrapolate to measure temperatures that are hotter or colder.) This is shown in Figure \(\PageIndex{4}\) .

Figure \(\PageIndex{4}\) – The Celsius scale was developed by setting 0 as the freezing point of water at 1 atm and setting 100 as the boiling point of water at 1 atm. This created a total number of 100 degrees between hot and cold. This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0. 

Celsius is a scientific scale because it’s repeatable. As long as two (or more) scientists use pure water, and freeze and melt that water at one atmosphere of pressure, they will develop identical temperature scales. Because of this, Celsius is the scale that we will use, almost exclusively, to discuss temperature in this textbook.

Although we will not be using the Fahrenheit scale in this textbook, it is still useful to understand how to convert between the Fahrenheit and Celsius scales. To convert between scales, we need to know where the two scales overlap with each other, and how much of a change in one scale relates to a change in the other scale. On the first point: 0 ^oC is equal to 32 ^oF. On the second point: a change in 1 ^oC is equal to a change in 1.8 ^oF. (Note the use of the symbol ^oC to denote a Celsius degree, which is used to distinguish a change in temperature from a temperature value.) Therefore, to convert from degrees Celsius to degrees Fahrenheit, take the temperature in Celsius, multiply by 1.8, and add 32:

\[T_F = 1.8 T_C + 32\]

To convert from degrees Fahrenheit to degrees Celsius, take the temperature in Fahrenheit and subtract 32 from it. Multiply the result of that subtraction by five-ninths. The result is the temperature in degrees Celsius:

\[T_C = \left(T_F-32\right)\times \frac{5}{9}\]

Thermometers

To measure temperature, a thermometer is used. How do thermometers work, and how are they designed?

In general, a thermometer exploits a thermometric property of a substance. A thermometric property is simply a property of the substance that varies with temperature. To achieve the best sensitivity for a thermometer, you want to choose a property that has a very large variation for small changes in temperature. Most analog thermometers (see, for example, Figure \(\PageIndex{5}\)) contain a substance that will remain a liquid at all temperatures that the thermometer can reasonably be expected to experience. For example, in geographic regions with hot summers and cold winters, a thermometer would need to remain liquid between temperatures of roughly -20 ^oC and +40 ^oC. Modern thermometers are generally filled with dyed ethyl alcohol, which remains liquid between temperatures of -114 ^oC and +78 ^oC. (Previously, thermometers were filled with mercury, which remains liquid to much higher temperatures, but which is a hazardous toxic element.)

Figure \(\PageIndex{5}\) – An analog thermometer uses a liquid that will remain in liquid form throughout a wide temperature range. This thermometer uses red dyed alcohol. This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

Materials such as liquids will generally expand as they heat and contract as they cool. That is, the thermometric property used is the volume of the substance. This means that as the thermometer is placed in cooler temperatures, the level of liquid will fall. As the thermometer is placed in hotter temperatures, the level of liquid will rise. To calibrate the thermometer, it can be placed in freezing water to establish the 0 ^oC point, placed in boiling water to determine the 100 ^oC point, and then 99 gradations placed in between. To determine the temperature at any given time, the level of liquid inside the thermometer can be read, as after a time it will have risen or fallen to the level corresponding to the current temperature.

 A digital thermometer (shown in Figure \(\PageIndex{6}\) , for example) has a device inside whose electrical properties are changed as a function of temperature. The thermometric property in this case of the resistivity of a semiconductor. The relationship between temperature and resistivity is well known. Therefore, by measuring the resistivity, the temperature can be determined. A microcontroller then converts that temperature into numbers and displays them on an LCD screen.

 

Figure \(\PageIndex{6}\) – A digital thermometer uses the relationship between temperature and electrical properties to determine the temperature. This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

Heat

Heat is energy that is transferred from one object to another in response to a difference in temperature. The symbol for heat is the uppercase letter \(Q\). Calories (cal) are the unit for heat. Because heat is a form of energy, joules is another unit that can be used to express heat.

Heat only spontaneously flows from hot to cold, and never spontaneously flows in the opposite direction. To relate this to something more familiar, consider it to be similar to gravity. If a ball is placed at the top of a ramp, gravity will pull the ball downward, causing it to roll down the ramp. Once the ball reaches the bottom of the ramp, gravity will not pull it back up to the top again. The only way for the ball to reach the top of the ramp is for a person, animal, or machine to expend energy in physically moving it back to the top again. Going against gravity requires work.

In much the same way, working against the established flow of heat takes work. Maybe you use a refrigerator or air conditioner. These seem to work against the flow of heat from hot to cold. And they do, but it requires energy to do this. If you’ve paid an electrical bill during a hot summer month when running the air conditioner, you know it’s not cheap to keep things cool. In other words, your refrigerator and air conditioner will not cool the regions you want unless you plug them in and turn them on!

The mechanisms through which heat can flow from one place to another will be the subject of the next chapter of this textbook.

Specific heat capacity

Specific heat capacity defines how difficult it is to change the temperature of a substance. (It can be thought of as “thermal inertia.”) The symbol for specific heat capacity is the lowercase letter \(c\). The unit is calories per gram degree Celsius (cal/(g^oC)). Specific heat capacity describes how many calories of heat are required to increase (or decrease) the temperature of a certain mass of material by a certain amount.

The equation that relates heat, specific heat capacity, mass, and change in temperature is

 \[Q=mc\Delta T \label{specificheateqn}\]

where \(Q\) is the heat (measured in calories), \(m\) is the mass (measured in grams),  is the specific heat capacity, and \(\Delta T\) is the temperature change (measured in degrees Celsius).

It is important to note that this equation only works when the temperature of a substance changes, and cannot be used when an item changes phase, for example to calculate the heat required to boil water.

The specific heat capacity of water is 1 cal/(g^oC). This means that 1 calorie of heat is required to raise the temperature of a single gram of water by one Celsius degree. (The calorie unit was actually defined on this basis; one calorie was equal to the amount of heat required to increase the temperature of one gram of water by one Celsius degree.) This may not seem like a lot, but water actually has one of the highest specific heat capacities of common substances. It makes water a very good candidate for use in cooling systems, because it can absorb a lot of heat without changing its temperature very much.

Definition: Large Calories and Small Calories

The unit of calorie may be familiar if you have looked at the nutrition label for food (such as the one shown in Figure \(\PageIndex{7}\)). The unit of calorie used in food products does relate to the amount of heat required to raise the temperature of water by one Celsius degree, however, in this case, the amount of water is one kilogram, not one gram! These calories are known as “large calories,” “food calories,” or “kilogram calories” and are sometimes specifically spelled out as Calories with a capital C to distinguish them from the so-called small calorie described above.

Figure \(\PageIndex{7}\) – A nutrition label indicates the calorie content of the food, which describes the amount of heat required to raise the temperature of one kilogram of water by one Celsius degree. This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

 This fact also explains why the climate tends to be milder if you live near a large body of water. This could be an ocean, or even a large lake such as Lake Michigan. Because the water in an ocean or lake doesn’t change its temperature easily, it means that the water will act as a moderating influence as the seasons change. This also explains why daily temperature fluctuations are much larger in the desert than they are in wetter climates. Humidity in the air acts as a moderating influence to keep temperatures from swinging to extremes between night and day. For example, Figure \(\PageIndex{8}\) shows the hourly temperature in Phoenix, AZ and Miami, FL on September 14, 2021. (Download this data [XLSX, 9 kB]) In Phoenix, a desert, the temperature demonstrates a much greater variation than in Miami, a much wetter climate.

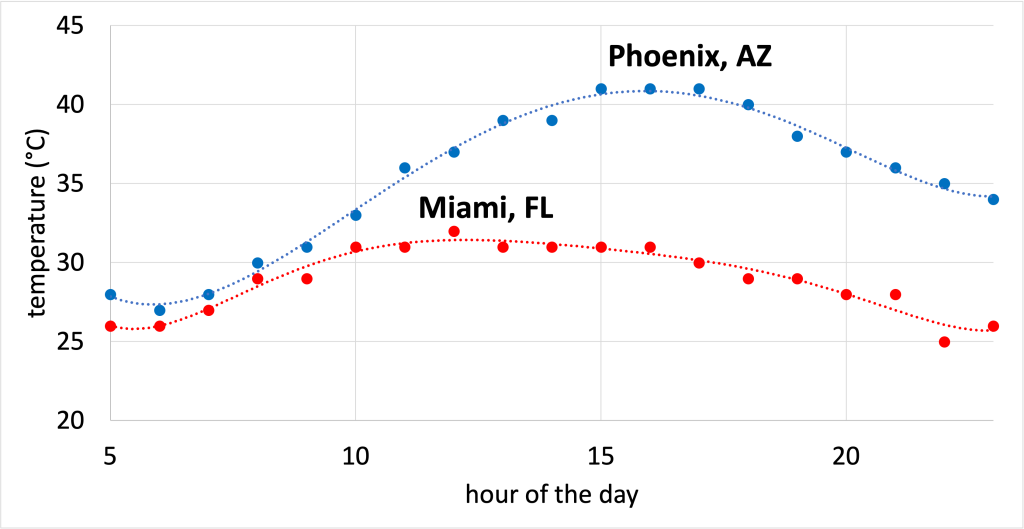
Figure \(\PageIndex{8}\) – The temperature in Phoenix, AZ (a desert) demonstrates a much wider range of temperatures than the temperature in Miami, FL (a humid climate). This data was taken on September 14, 2021. This figure, created by Alyssa J. Pasquale, Ph.D., is licensed under CC BY-NC-SA 4.0.

Temperature mixtures

When two substances at different initial temperatures are combined together, the hot substance will cool down and the cool substance will heat up until the two substances arrive at thermal equilibrium. At this point the temperature will remain constant. According to the law of conservation of energy, the energy that is lost by the hot substance will be completely transferred to the cool substance. (This assumes that no heat is lost to the surroundings.) In equation form,

\[-Q_{hot}=Q_{cold}\]

\[Q_{hot}+Q_{cold}=0\]

Unless the two substances are composed of the same material with identical specific heat capacities and have the same mass, while both substances will experience a temperature change, the magnitude of change in temperature of each substance may not be the same. (For example, if the hot substance cools down by 10 C^o, the cool object may not warm up by that same amount.) All other things being equal, a substance with a higher specific heat capacity will experience a smaller temperature change than a substance with a lower specific heat capacity.

To determine the final temperature of a mixture of two substances, the conservation of energy equation defined above can be substituted with \(Q=mc\Delta T\) to calculate \(T_{final}\). This equation is

\[T_{final}=\frac{m_h c_h T_{i,h}+m_c c_c T_{i,c}}{m_h c_h+m_c c_c}\]

In this equation, subscript \(i\) indicates initial conditions, \(h\) is for the initially hot substance, and \(c\) is for the initially cold substance. The final temperature should be somewhere in between the two initial starting temperatures. (This is a good “smell test” to use to determine if your final temperature calculation makes sense.)

PhET Exploration: Heat Transfer and Specific Heat Capacity

Below is a simulation that demonstrates the specific heat capacity of water compared to olive oil. Click on the "Intro" tab. Notice there are equal volumes of water and olive oil in two separate beakers. Water and olive oil have similar densities (mass per volume of ~1 gram/cm³). Therefore, the masses are nearly equal too! Place each beaker on a heater stand. Click the "Energy Symbols" and "Link Heaters" buttons. Then, drag one of the sliders to "Heat".

1. What do you notice about the number of energy symbols that are transferring from the flame to the water and olive oil? Are they equal amounts of heat, \(Q\)?
2. How does the temperature change for each substance over equal amounts of time?
3. If in number 1, there were equal amounts of energy, how can you use equation \ref{specificheateqn} to explain the differences in temperature change between water and olive oil?
   1. Which substance has a higher specific heat capacity? Explain.
4. Try one of the other substances (iron or brick). How does its specific heat capacity compare to water? Explain.