7.1: Precipitation and Dissolution
- Page ID
- 31565
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Write chemical equations and equilibrium expressions representing solubility equilibria
- Carry out equilibrium computations involving solubility, equilibrium expressions, and solute concentrations
The preservation of medical laboratory blood samples, mining of sea water for magnesium, formulation of over-the-counter medicines such as Milk of Magnesia and antacids, and treating the presence of hard water in your home’s water supply are just a few of the many tasks that involve controlling the equilibrium between a slightly soluble ionic solid and an aqueous solution of its ions.
In some cases, we want to prevent dissolution from occurring. Tooth decay, for example, occurs when the calcium hydroxylapatite, which has the formula Ca5(PO4)3(OH), in our teeth dissolves. The dissolution process is aided when bacteria in our mouths feast on the sugars in our diets to produce lactic acid, which reacts with the hydroxide ions in the calcium hydroxylapatite. Preventing the dissolution prevents the decay. On the other hand, sometimes we want a substance to dissolve. We want the calcium carbonate in a chewable antacid to dissolve because the \(\ce{CO3^2-}\) ions produced in this process help soothe an upset stomach.
In this section, we will find out how we can control the dissolution of a slightly soluble ionic solid by the application of Le Chatelier’s principle. We will also learn how to use the equilibrium constant of the reaction to determine the concentration of ions present in a solution.
The Solubility Product Constant
Silver chloride is what’s known as a sparingly soluble ionic solid (Figure \(\PageIndex{1}\)). Halides of Ag+ are not normally soluble. However, when we add an excess of solid AgCl to water, it dissolves to a small extent and produces a mixture consisting of a very dilute solution of Ag+ and Cl– ions in equilibrium with undissolved silver chloride:
\[\ce{AgCl}(s)\mathrm{\xrightleftharpoons[\:precipitation\:]{\:dissolution\:}}\ce{Ag+}(aq)+\ce{Cl-}(aq)\]
This equilibrium, like other equilibria, is dynamic; some of the solid AgCl continues to dissolve, but at the same time, Ag+ and Cl– ions in the solution combine to produce an equal amount of the solid. At equilibrium, the opposing processes have equal rates.
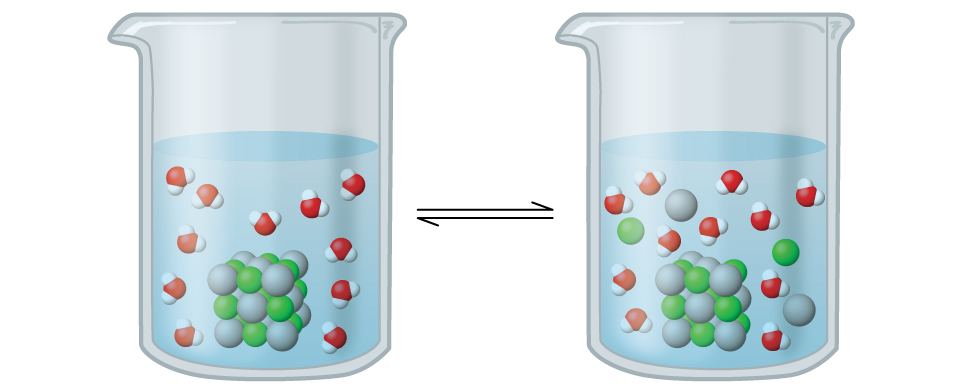
The equilibrium constant for the equilibrium between a slightly soluble ionic solid and a solution of its ions is called the solubility product (Ksp) of the solid. Recall that we use an ion’s concentration as an approximation of its activity in a dilute solution. For silver chloride, at equilibrium:
\[\ce{AgCl}(s) \rightleftharpoons \ce{Ag+}(aq)+\ce{Cl-}(aq) \]
with
\[K_\ce{sp}=[\ce{Ag+}(aq)][\ce{Cl-}(aq)]\]
When looking at dissolution reactions such as this, the solid is listed as a reactant, whereas the ions are listed as products. In other words, always write these reactions as dissolution reactions! The solubility product constant, as with every equilibrium constant expression, is written as the product of the concentrations of each of the ions, raised to the power of their stoichiometric coefficients from the balanced reaction. Here, the solubility product constant is equal to the product of [Ag+] and [Cl–] when a solution of silver chloride is in equilibrium with undissolved AgCl. There is no denominator representing the reactants in this equilibrium expression since the reactant is a pure solid; therefore [AgCl] does not appear in the expression for Ksp (the activity of a pure solid is defined as 1).
| Substance | Ksp at 25 °C |
|---|---|
| CuCl | 1.2 × 10–6 |
| CuBr | 6.27 × 10–9 |
| AgI | 1.5 × 10–16 |
| PbS | 7 × 10–29 |
| Al(OH)3 | 2 × 10–32 |
| Fe(OH)3 | 4 × 10–38 |
Some common solubility products are listed in Table \(\PageIndex{1}\) according to their Ksp values. Each of these equilibrium constants is much smaller than 1 because the compounds listed are only slightly soluble. A small Ksp represents a system in which the equilibrium lies to the left (the solid form), so that relatively few hydrated ions would be present in a saturated solution.
Example \(\PageIndex{1}\): Writing Equations and Solubility Products
Write the ionic equation for the dissolution and the solubility product expression for each of the following slightly soluble ionic compounds:
- AgI, silver iodide, a solid with antiseptic properties
- CaCO3, calcium carbonate, the active ingredient in many over-the-counter chewable antacids
- Mg(OH)2, magnesium hydroxide, the active ingredient in Milk of Magnesia
- Mg(NH4)PO4, magnesium ammonium phosphate, an essentially insoluble substance used in tests for magnesium
- Ca5(PO4)3OH, the mineral apatite, a source of phosphate for fertilizers
(For d. and e., common ions such as ammonium, phosphate, and hydroxide will remain intact after dissolution of the parent compound.)
Solution
- \(\ce{AgI}(s) \rightleftharpoons \ce{Ag+}(aq)+\ce{I-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Ag+][I- ]}\)
- \(\ce{CaCO3}(s) \rightleftharpoons \ce{Ca^2+}(aq)+\ce{CO3^2-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Ca^2+][CO3^2- ]}\)
- \(\ce{Mg(OH)2}(s) \rightleftharpoons \ce{Mg^2+}(aq)+\ce{2OH-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Mg^2+][OH- ]^2}\)
- \(\ce{Mg(NH4)PO4}(s) \rightleftharpoons \ce{Mg^2+}(aq)+\ce{NH4+}(aq)+\ce{PO4^3-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Mg^2+][NH4+][PO4^3- ]}\)
- \(\ce{Ca5(PO4)3OH}(s) \rightleftharpoons \ce{5Ca^2+}(aq)+\ce{3PO4^3-}(aq)+\ce{OH-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Ca^2+]^5[PO4^3- ]^3[OH- ]}\)
Exercise \(\PageIndex{1}\)
Write the ionic equation for the dissolution and the solubility product for each of the following slightly soluble compounds:
- BaSO4
- Ag2SO4
- Al(OH)3
- Pb(OH)Cl
- Answer a
-
\(\ce{BaSO4}(s) \rightleftharpoons \ce{Ba^2+}(aq)+\ce{SO4^2-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Ba^2+][SO4^2- ]}\)
- Answer b
-
\(\ce{Ag2SO4}(s) \rightleftharpoons \ce{2Ag+}(aq)+\ce{SO4^2-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Ag+]^2[SO4^2- ]}\)
- Answer c
-
\(\ce{Al(OH)3}(s) \rightleftharpoons \ce{Al^2+}(aq)+\ce{3OH-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Al^3+][OH- ]^3}\)
- Answer d
-
\(\ce{Pb(OH)Cl}(s) \rightleftharpoons \ce{Pb^2+}(aq)+\ce{OH-}(aq)+\ce{Cl-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Pb^2+][OH- ][Cl- ]}\)
Now we will extend the discussion of Ksp and show how the solubility product constant is determined from the solubility of its ions, as well as how Ksp can be used to determine the molar solubility of a substance.
Ksp and Solubility
The definition of solubility is the maximum possible concentration of a solute in a solution at a given temperature and pressure. We can determine the solubility product of a slightly soluble solid from that measure of its solubility at a given temperature and pressure, provided that the only significant reaction that occurs when the solid dissolves is its dissociation into solvated ions, that is, the only equilibrium involved is:
\[\ce{M}_p\ce{X}_q(s) \rightleftharpoons p\mathrm{M^{m+}}(aq)+q\mathrm{X^{n−}}(aq)\]
In this case, we calculate the solubility product by taking the solid’s solubility expressed in units of moles per liter (mol/L), known as its molar solubility.
Example \(\PageIndex{2}\): Calculation of Ksp from Equilibrium Concentrations
We began the chapter with an informal discussion of how the mineral fluorite is formed. Fluorite, CaF2, is a slightly soluble solid that dissolves according to the equation:
\[\ce{CaF2}(s) \rightleftharpoons \ce{Ca^2+}(aq)+\ce{2F-}(aq) \nonumber \]
The concentration of Ca2+ in a saturated solution of CaF2 is 2.1 × 10–4 M; therefore, that of F– is 4.2 × 10–4 M, that is, twice the concentration of Ca2+. What is the solubility product of fluorite?
Solution
A saturated solution is a solution at equilibrium with the solid. Thus the reaction, as above, is:
\[\ce{CaF2}(s) \rightleftharpoons \ce{Ca^2+}(aq)+\ce{2F-}(aq) \nonumber\]
Write out the Ksp expression, then substitute in concentrations and solve for Ksp.
\[K_\ce{sp}=\ce{[Ca^2+][F^{-}]^2}=(2.1×10^{−4})(4.2×10^{−4})^2=3.7×10^{−11} \nonumber\]
As with other equilibrium constants, we do not include units with Ksp.
Exercise \(\PageIndex{2}\)
In a saturated solution that is in contact with solid Mg(OH)2, the concentration of Mg2+ is 3.7 × 10–5 M. What is the solubility product for Mg(OH)2?
\[\ce{Mg(OH)2}(s) \rightleftharpoons \ce{Mg^2+}(aq)+\ce{2OH-}(aq) \nonumber\]
- Answer
-
2.0 × 10–13
Example \(\PageIndex{3}\): Determination of Molar Solubility from Ksp
The Ksp of copper(I) bromide, CuBr, is 6.3 × 10–9. Calculate the molar solubility of copper bromide.
Solution
The solubility product constant of copper(I) bromide is 6.3 × 10–9.
The reaction is:
\[\ce{CuBr}(s) \rightleftharpoons \ce{Cu+}(aq)+\ce{Br-}(aq) \nonumber\]
First, write out the solubility product equilibrium constant expression:
\[K_\ce{sp}=\ce{[Cu+][Br- ]} \nonumber\]
At equilibrium:
Therefore, the molar solubility of CuBr is 7.9 × 10–5 M.
Exercise \(\PageIndex{3}\)
The Ksp of AgI is 1.5 × 10–16. Calculate the molar solubility of silver iodide.
- Answer
-
1.2 × 10–8 M
Example \(\PageIndex{4}\): Determination of Molar Solubility from Ksp, Part II
Determination of Molar Solubility from Ksp, Part II The Ksp of calcium hydroxide, Ca(OH)2, is 8.0 × 10–6. Calculate the molar solubility of calcium hydroxide.
Solution
The solubility product constant of calcium hydroxide is 1.3 × 10–6.
The reaction is:
\[\ce{Ca(OH)2}(s) \rightleftharpoons \ce{Ca^2+}(aq)+\ce{2OH-}(aq) \nonumber\]
First, write out the solubility product equilibrium constant expression:
\[K_\ce{sp}=\ce{[Ca^2+][OH- ]^2} \nonumber\]
At equilibrium:
\(K_\ce{sp}=\ce{[Ca^2+][OH- ]^2}\)
\(1.3×10^{−6}=(x)(2x)^2=(x)(4x^2)=4x^3\)
\(x=\sqrt[3]{\dfrac{1.3×10^{-6}}{4}}=6.9×10^{-3}\)
Therefore, the molar solubility of Ca(OH)2 is 6.9 × 10–3 M.
Exercise \(\PageIndex{4}\)
The Ksp of PbI2 is 1.4 × 10–8. Calculate the molar solubility of lead(II) iodide.
- Answer
-
1.5 × 10–3 M
Note that solubility is not always given as a molar value. When the solubility of a compound is given in some unit other than moles per liter, we must convert the solubility into moles per liter (i.e., molarity) in order to use it in the solubility product constant expression. Example \(\PageIndex{5}\) shows how to perform those unit conversions before determining the solubility product equilibrium.
Example \(\PageIndex{5}\): Determination of Ksp from Gram Solubility
Many of the pigments used by artists in oil-based paints (Figure \(\PageIndex{2}\)) are sparingly soluble in water. For example, the solubility of the artist’s pigment chrome yellow, PbCrO4, is 4.6 × 10–6 g/L. Determine the solubility product equilibrium constant for PbCrO4.

Solution
We are given the solubility of PbCrO4 in grams per liter. If we convert this solubility into moles per liter, we can find the equilibrium concentrations of Pb2+ and \(\ce{CrO4^2-}\), then Ksp:

- Use the molar mass of PbCrO4 \(\mathrm{\left(\dfrac{323.2\:g}{1\:mol}\right)}\) to convert the solubility of PbCrO4 in grams per liter into moles per liter:
\(\mathrm{[PbCrO_4]=\dfrac{4.6×10^{−6}\:g\: PbCrO_4}{1\:L}×\dfrac{1\:mol\: PbCrO_4}{323.2\:g\: PbCrO_4}}\)
\(\mathrm{=\dfrac{1.4×10^{−8}\:mol\: PbCrO_4}{1\:L}}\)
\(=1.4×10^{−8}\:M\)
- The chemical equation for the dissolution indicates that 1 mol of PbCrO4 gives 1 mol of Pb2+(aq) and 1 mol of \(\ce{CrO_4^{2-}}(aq)\):
\(\ce{PbCrO4}(s) \rightleftharpoons \ce{Pb^2+}(aq)+\ce{CrO4^2-}(aq)\)
Thus, both [Pb2+] and \(\ce{[CrO4^2- ]}\) are equal to the molar solubility of PbCrO4:
\(\ce{[Pb^2+]}=\ce{[CrO4^2- ]}=1.4×10^{−8}\:M\) - Solve. Ksp = [Pb2+] \(\ce{[CrO4^2- ]}\) = (1.4 × 10–8)(1.4 × 10–8) = 2.0 × 10–16
Exercise \(\PageIndex{5}\)
The solubility of TlCl [thallium(I) chloride], an intermediate formed when thallium is being isolated from ores, is 3.46 grams per liter at 20 °C. What is its solubility product?
- Answer
-
2.08 × 10–4
Using Barium Sulfate for Medical Imaging
Various types of medical imaging techniques are used to aid diagnoses of illnesses in a noninvasive manner. One such technique utilizes the ingestion of a barium compound before taking an X-ray image. A suspension of barium sulfate, a chalky powder, is ingested by the patient. Since the Ksp of barium sulfate is 1.1 × 10–10, very little of it dissolves as it coats the lining of the patient’s intestinal tract. Barium-coated areas of the digestive tract then appear on an X-ray as white, allowing for greater visual detail than a traditional X-ray (Figure \(\PageIndex{3}\)).

Further diagnostic testing can be done using barium sulfate and fluoroscopy. In fluoroscopy, a continuous X-ray is passed through the body so the doctor can monitor, on a TV or computer screen, the barium sulfate’s movement as it passes through the digestive tract. Medical imaging using barium sulfate can be used to diagnose acid reflux disease, Crohn’s disease, and ulcers in addition to other conditions.
Predicting Precipitation
Tabulated Ksp values can also be compared to reaction quotients calculated from experimental data to tell whether a solid will precipitate in a reaction under specific conditions: Q equals Ksp at equilibrium; if Q is less than Ksp, the solid will dissolve until Q equals Ksp; if Q is greater than Ksp, precipitation will occur at a given temperature until Q equals Ksp.
The equation that describes the equilibrium between solid calcium carbonate and its solvated ions is:
\[\ce{CaCO3}(s) \rightleftharpoons \ce{Ca^2+}(aq)+\ce{CO3^2-}(aq)\]
We can establish this equilibrium either by adding solid calcium carbonate to water or by mixing a solution that contains calcium ions with a solution that contains carbonate ions. If we add calcium carbonate to water, the solid will dissolve until the concentrations are such that the value of the reaction quotient \(\ce{(Q=[Ca^2+][CO3^2- ])}\) is equal to the solubility product (Ksp = 4.8 × 10–9). If we mix a solution of calcium nitrate, which contains Ca2+ ions, with a solution of sodium carbonate, which contains \(\ce{CO3^2-}\) ions, the slightly soluble ionic solid CaCO3 will precipitate, provided that the concentrations of Ca2+ and \(\ce{CO3^2-}\) ions are such that Q is greater than Ksp for the mixture. The reaction shifts to the left and the concentrations of the ions are reduced by formation of the solid until the value of Q equals Ksp. A saturated solution in equilibrium with the undissolved solid will result. If the concentrations are such that Q is less than Ksp, then the solution is not saturated and no precipitate will form.
We can compare numerical values of Q with Ksp to predict whether precipitation will occur, as Example \(\PageIndex{7}\) shows. (Note: Since all forms of equilibrium constants are temperature dependent, we will assume a room temperature environment going forward in this chapter unless a different temperature value is explicitly specified.)
Example \(\PageIndex{7}\): Precipitation of Mg(OH)2
The first step in the preparation of magnesium metal is the precipitation of Mg(OH)2 from sea water by the addition of lime, Ca(OH)2, a readily available inexpensive source of OH– ion:
\[\ce{Mg(OH)2}(s) \rightleftharpoons \ce{Mg^2+}(aq)+\ce{2OH-}(aq) \hspace{20px} K_\ce{sp}=8.9×10^{−12}\]
The concentration of Mg2+(aq) in sea water is 0.0537 M. Will Mg(OH)2 precipitate when enough Ca(OH)2 is added to give a [OH–] of 0.0010 M?
Solution
This problem asks whether the reaction:
\[\ce{Mg(OH)2}(s) \rightleftharpoons \ce{Mg^2+}(aq)+\ce{2OH-}(aq)\]
shifts to the left and forms solid Mg(OH)2 when [Mg2+] = 0.0537 M and [OH–] = 0.0010 M. The reaction shifts to the left if Q is greater than Ksp. Calculation of the reaction quotient under these conditions is shown here:
\[\mathrm{Q=[Mg^{2+}][OH^-]^2=(0.0537)(0.0010)^2=5.4×10^{−8}}\]
Because Q is greater than Ksp (Q = 5.4 × 10–8 is larger than Ksp = 8.9 × 10–12), we can expect the reaction to shift to the left and form solid magnesium hydroxide. Mg(OH)2(s) forms until the concentrations of magnesium ion and hydroxide ion are reduced sufficiently so that the value of Q is equal to Ksp.
Exercise \(\PageIndex{7}\)
Use the solubility products in Table E3 to determine whether CaHPO4 will precipitate from a solution with [Ca2+] = 0.0001 M and \(\ce{[HPO4^2- ]}\) = 0.001 M.
- Answer
-
No precipitation of CaHPO4; Q = 1 × 10–7, which is less than Ksp
Example \(\PageIndex{8}\): Precipitation of AgCl upon Mixing Solutions
Does silver chloride precipitate when equal volumes of a 2.0 × 10–4-M solution of AgNO3 and a 2.0 × 10–4-M solution of NaCl are mixed?
(Note: The solution also contains Na+ and \(\ce{NO3-}\) ions, but when referring to solubility rules, one can see that sodium nitrate is very soluble and cannot form a precipitate.)
Solution
The equation for the equilibrium between solid silver chloride, silver ion, and chloride ion is:
The solubility product is 1.8 × 10–10 (Table E3).
AgCl will precipitate if the reaction quotient calculated from the concentrations in the mixture of AgNO3 and NaCl is greater than Ksp. The volume doubles when we mix equal volumes of AgNO3 and NaCl solutions, so each concentration is reduced to half its initial value. Consequently, immediately upon mixing, [Ag+] and [Cl–] are both equal to:
The reaction quotient, Q, is momentarily greater than Ksp for AgCl, so a supersaturated solution is formed:
Since supersaturated solutions are unstable, AgCl will precipitate from the mixture until the solution returns to equilibrium, with Q equal to Ksp.
Exercise \(\PageIndex{8}\)
Will KClO4 precipitate when 20 mL of a 0.050-M solution of K+ is added to 80 mL of a 0.50-M solution of \(\ce{ClO4-}\)? (Remember to calculate the new concentration of each ion after mixing the solutions before plugging into the reaction quotient expression.)
- Answer
-
No, Q = 4.0 × 10–3, which is less than Ksp = 1.07 × 10–2
In the previous two examples, we have seen that Mg(OH)2 or AgCl precipitate when Q is greater than Ksp. In general, when a solution of a soluble salt of the Mm+ ion is mixed with a solution of a soluble salt of the Xn– ion, the solid, MpXq precipitates if the value of Q for the mixture of Mm+ and Xn– is greater than Ksp for MpXq. Thus, if we know the concentration of one of the ions of a slightly soluble ionic solid and the value for the solubility product of the solid, then we can calculate the concentration that the other ion must exceed for precipitation to begin. To simplify the calculation, we will assume that precipitation begins when the reaction quotient becomes equal to the solubility product constant.
Example \(\PageIndex{9}\): Precipitation of Calcium Oxalate
Blood will not clot if calcium ions are removed from its plasma. Some blood collection tubes contain salts of the oxalate ion, \(\ce{C2O4^2-}\), for this purpose (Figure \(\PageIndex{4}\)). At sufficiently high concentrations, the calcium and oxalate ions form solid, CaC2O4•H2O (which also contains water bound in the solid). The concentration of Ca2+ in a sample of blood serum is 2.2 × 10–3 M. What concentration of \(\ce{C2O4^2-}\) ion must be established before CaC2O4•H2O begins to precipitate?

Solution
The equilibrium expression is:
For this reaction (Table E3):
CaC2O4 does not appear in this expression because it is a solid. Water does not appear because it is the solvent.
Solid CaC2O4 does not begin to form until Q equals Ksp. Because we know Ksp and [Ca2+], we can solve for the concentration of \(\ce{C2O4^2-}\) that is necessary to produce the first trace of solid:
A concentration of \(\ce{[C2O4^2- ]}\) = 8.9 × 10–6 M is necessary to initiate the precipitation of CaC2O4 under these conditions.
Exercise \(\PageIndex{9}\)
If a solution contains 0.0020 mol of \(\ce{CrO4^2-}\) per liter, what concentration of Ag+ ion must be reached by adding solid AgNO3 before Ag2CrO4 begins to precipitate? Neglect any increase in volume upon adding the solid silver nitrate.
- Answer
-
4.5 × 10–9 M
It is sometimes useful to know the concentration of an ion that remains in solution after precipitation. We can use the solubility product for this calculation too: If we know the value of Ksp and the concentration of one ion in solution, we can calculate the concentration of the second ion remaining in solution. The calculation is of the same type as that in Example \(\PageIndex{8}\)—calculation of the concentration of a species in an equilibrium mixture from the concentrations of the other species and the equilibrium constant. However, the concentrations are different; we are calculating concentrations after precipitation is complete, rather than at the start of precipitation.
Example \(\PageIndex{10}\): Concentrations Following Precipitation
Clothing washed in water that has a manganese [Mn2+(aq)] concentration exceeding 0.1 mg/L (1.8 × 10–6 M) may be stained by the manganese upon oxidation, but the amount of Mn2+ in the water can be reduced by adding a base. If a person doing laundry wishes to add a buffer to keep the pH high enough to precipitate the manganese as the hydroxide, Mn(OH)2, what pH is required to keep [Mn2+] equal to 1.8 × 10–6 M?
Solution
The dissolution of Mn(OH)2 is described by the equation:
\[\ce{Mn(OH)2}(s) \rightleftharpoons \ce{Mn^2+}(aq)+\ce{2OH-}(aq) \hspace{20px} K_\ce{sp}=2×10^{−13}\]
We need to calculate the concentration of OH– when the concentration of Mn2+ is 1.8 × 10–6 M. From that, we calculate the pH. At equilibrium:
or
so
Now we calculate the pH from the pOH:
If the person doing laundry adds a base, such as the sodium silicate (Na4SiO4) in some detergents, to the wash water until the pH is raised to 10.52, the manganese ion will be reduced to a concentration of 1.8 × 10–6 M; at that concentration or less, the ion will not stain clothing.
Exercise \(\PageIndex{10}\)
The first step in the preparation of magnesium metal is the precipitation of Mg(OH)2 from sea water by the addition of Ca(OH)2. The concentration of Mg2+(aq) in sea water is 5.37 × 10–2 M. Calculate the pH at which [Mg2+] is diminished to 1.0 × 10–5 M by the addition of Ca(OH)2.
- Answer
-
10.97
Due to their light sensitivity, mixtures of silver halides are used in fiber optics for medical lasers, in photochromic eyeglass lenses (glass lenses that automatically darken when exposed to sunlight), and—before the advent of digital photography—in photographic film. Even though AgCl (Ksp = 1.6 × 10–10), AgBr (Ksp = 5.0 × 10–13), and AgI (Ksp = 1.5 × 10–16) are each quite insoluble, we cannot prepare a homogeneous solid mixture of them by adding Ag+ to a solution of Cl–, Br–, and I–; essentially all of the AgI will precipitate before any of the other solid halides form because of its smaller value for Ksp. However, we can prepare a homogeneous mixture of the solids by slowly adding a solution of Cl–, Br–, and I– to a solution of Ag+.
When two anions form slightly soluble compounds with the same cation, or when two cations form slightly soluble compounds with the same anion, the less soluble compound (usually, the compound with the smaller Ksp) generally precipitates first when we add a precipitating agent to a solution containing both anions (or both cations). When the Ksp values of the two compounds differ by two orders of magnitude or more (e.g., 10–2 vs. 10–4), almost all of the less soluble compound precipitates before any of the more soluble one does. This is an example of selective precipitation, where a reagent is added to a solution of dissolved ions causing one of the ions to precipitate out before the rest.
The Role of Precipitation in Wastewater Treatment
Solubility equilibria are useful tools in the treatment of wastewater carried out in facilities that may treat the municipal water in your city or town (Figure \(\PageIndex{5}\)). Specifically, selective precipitation is used to remove contaminants from wastewater before it is released back into natural bodies of water. For example, phosphate ions \(\ce{(PO4^2- )}\) are often present in both municipal and industrial wastewaters. An abundance of phosphate causes excess algae to grow, which impacts the amount of oxygen available for marine life as well as making water unsuitable for human consumption.

One common way to remove phosphates from wastewater is by the addition of calcium hydroxide, known as lime, Ca(OH)2. The lime is converted into calcium carbonate, a strong base, in the water. As the water is made more basic, the calcium ions react with phosphate ions to produce hydroxylapatite, Ca5(PO4)3(OH), which then precipitates out of the solution:
\[\ce{5Ca^2+ + 3PO4^3- + OH- \rightleftharpoons Ca10(PO4)6⋅(OH)2}(s)\]
The precipitate is then removed by filtration and the water is brought back to a neutral pH by the addition of CO2 in a recarbonation process. Other chemicals can also be used for the removal of phosphates by precipitation, including iron(III) chloride and aluminum sulfate ("alum").
Contributors and Attributions
Summary
The equilibrium constant for an equilibrium involving the precipitation or dissolution of a slightly soluble ionic solid is called the solubility product, Ksp, of the solid. When we have a heterogeneous equilibrium involving the slightly soluble solid MpXq and its ions Mm+ and Xn–:
\[\ce{M}_p\ce{X}_q(s) \rightleftharpoons p\mathrm{M^{m+}}(aq)+q\mathrm{X^{n−}}(aq) \nonumber\]
We write the solubility product expression as:
\[K_\ce{sp}=\mathrm{[M^{m+}]}^p\mathrm{[X^{n−}]}^q \nonumber\]
The solubility product of a slightly soluble electrolyte can be calculated from its solubility; conversely, its solubility can be calculated from its Ksp, provided the only significant reaction that occurs when the solid dissolves is the formation of its ions. A slightly soluble electrolyte begins to precipitate when the magnitude of the reaction quotient for the dissolution reaction exceeds the magnitude of the solubility product. Precipitation continues until the reaction quotient equals the solubility product. A reagent can be added to a solution of ions to allow one ion to selectively precipitate out of solution.
Glossary
- molar solubility
- solubility of a compound expressed in units of moles per liter (mol/L)
- olubility product (Ksp)
- equilibrium constant for the dissolution of a slightly soluble electrolyte


