8.1: Metals Complexation in Aqueous Solution
- Page ID
- 40123
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Define the terms coordination complex, ligand, polydentate, and chelate.
- Explain the origins of d-orbital splitting; that is, why the energies of certain atomic-d orbitals are more affected by some ligands than others in an octahedral complex.
- Why are many coordination complexes highly colored?
Complexes such as Cu(NH3)62+ have been known and studied since the mid-nineteenth century, and their structures had been mostly worked out by 1900. Although the hybrid orbital model was able to explain how neutral molecules such as water or ammonia could bond to a transition metal ion, it failed to explain many of the special properties of these complexes. Finally, in 1940-60, a model known as ligand field theory was developed that is able to organize and explain most of the observed properties of these compounds. Since that time, coordination complexes have played major roles in cellular biochemistry, inorganic catalysis, and metal speciation in environmental systems.
What is a Complex?
If you have taken a lab course in chemistry, you have very likely admired the deep blue color of copper sulfate crystals, CuSO4·5H2O. The proper name of this substance is copper(II) sulfate pentahydrate, and it is typical of many salts that incorporate waters of hydration into their crystal structures. It is also a complex, a term used by chemists to describe a substance composed of two other substances (in this case, CuSO4 and H2O) each of which is capable of an independent existence.


The binding between the components of a complex is usually weaker than a regular chemical bond; thus most solid hydrates can be decomposed by heating, driving off the water and yielding the anhydrous salt:
\[\underbrace{\ce{CuSO4 \cdot 5 H2O}}_{\text{blue}} \rightarrow \underbrace{\ce{CuSO_{4 (s)}}}_{\text{white}} + 5 H_2O\]
Driving off the water in this way also destroys the color, turning it from a beautiful deep blue to a nondescript white. If the anhydrous salt is now dissolved in water, the blue color now pervades the entire solution. It is apparent that the presence of water is somehow necessary for the copper(II) ion to take on a blue color, but why should this be?
-sulfate.jpg?revision=1)
A very common lab experiment that most students carry out is to add some dilute ammonia to a copper sulfate solution. At first, the solution turns milky as the alkaline ammonia causes the precipitation of copper hydroxide:
\[\ce{Cu^{2+} + 2 OH^{–} \rightarrow Cu(OH)2 (s)}\]
(The same precipitation could be carried out by adding a strong base such as NaOH, as shown in the video below.)
However, if more ammonia is added, the cloudiness disappears and the solution assumes an intense deep blue color that makes the original solution seem pale by comparison. The equation for this reaction is usually given as
\[\ce{Cu^{2+} + 6 NH3 \rightarrow Cu(NH3)6^{2+} } \label{ammine}\]
The new product is commonly known as the copper-ammonia complex ion, or more officially, hexamminecopper(II) complex ion.
Equation \(\ref{ammine}\) is somewhat misleading, however, in that it implies the formation of a new complex where none existed before. In fact, since about 1895, it has been known that the ions of most transition metals dissolve in water to form complexes with water itself, so a better representation of the reaction of dissolved copper with ammonia would be
\[\ce{Cu(H2O)6^{2+} + 6 NH3 \rightarrow Cu(NH3)6^{2+} + 6 H2O}\]
In effect, the ammonia binds more tightly to the copper ion than does water, and it thus displaces the latter when it comes into contact with the hexaaquocopper(II) ion, as the dissolved form of Cu2+ is properly known.
Most transition metals dissolve in water to form complexes with water itself.
The basics of Coordination Complexes
Although our primary focus in this unit is on bonding, the topic of coordination complexes is so important in chemistry and biochemistry that some of their basic features are worth knowing about, even if their detailed chemistry is beyond the scope of this course. These complexes play an especially crucial role in physiology and biochemistry. Thus heme, the oxygen-carrying component of red blood cells (and the source of the red color) is basically a complex of iron, and the part of chlorophyll that converts sunlight into chemical energy within green plants is a magnesium complex.
Some Definitions
We have already defined a complex as a substance composed of two or more components capable of an independent existence. A coordination complex is one in which a central atom or ion is joined to one or more ligands (Latin ligare, to tie) through what is called a coordinate covalent bond in which both of the bonding electrons are supplied by the ligand. In such a complex the central atom acts as an electron-pair acceptor (Lewis acid — think of H+ which has no electrons at all, but can accept a pair from something like Cl–) and the ligand as an electron-pair donor (Lewis base ). The central atom and the ligands coordinated to it constitute the coordination sphere. Thus the salt [Co(NH3)5Cl]Cl2 is composed of the complex ion [Co(NH3)5Cl]2+ and two Cl– ions; components within the square brackets are inside the coordination sphere, whereas the two chloride ions are situated outside the coordination sphere. These latter two ions could be replaced by other ions such as NO3– without otherwise materially changing the nature of the complex.
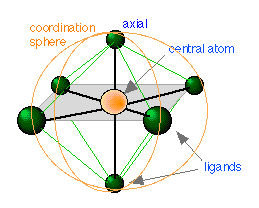
The central atoms of coordination complexes are most often cations (positive ions), but may in some cases be neutral atoms, as in nickel carbonyl Ni(CO)4.
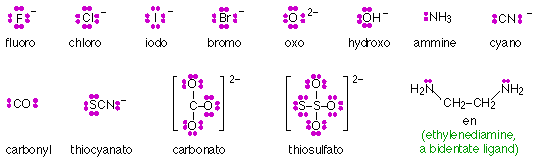
Ligands composed of ions such as F– or small molecules such as H2O or CN– possess more than one set of lone pair electrons, but only one of these pairs can coordinate with a central ion. Such ligands are said to be monodentate (“one tooth”.) Larger ligands may contain more than one atom capable of coordinating with a single central ion, and are described as polydentate. Thus ethylenediamine (shown below) is a bidentate ligand. Polydentate ligands whose geometry enables them to occupy more than one coordinating position of a central ion act as chelating agents (Greek χελος, chelos, claw) and tend to form extremely stable complexes known as chelates.
Chelation is widely employed in medicine, water-treatment, analytical chemistry and industry for binding and removing metal ions of particular kinds. Some of the more common ligands (chelating agents) are shown here:
Structure and bonding in transition metal complexes
Complexes such as Cu(NH3)62+ have been known and studied since the mid-nineteenth century. Why they should form, or what their structures might be, were complete mysteries. At that time all inorganic compounds were thought to be held together by ionic charges, but ligands such as water or ammonia are of course electrically neutral. A variety of theories such as the existence of “secondary valences” were concocted, and various chain-like structures such as CuNH3-NH3-NH3-NH3-NH3-NH3 were proposed. Finally, in the mid-1890s, after a series of painstaking experiments, the chemist Alfred Werner (Swiss, 1866-1919) presented the first workable theory of complex ion structures.
Werner claimed that his theory first came to him in a flash after a night of fitful sleep; by the end of the next day he had written his landmark paper that eventually won him the 1913 Nobel Prize in Chemistry.
What holds them together?
An understanding of the nature of the bond between the central ion and its ligands would have to await the development of Lewis’ shared-electron pair theory and Pauling’s valence-bond picture. Hybridization of the d orbitals of the central ion creates vacancies able to accommodate one or more pairs of unshared electrons on the ligands. Although these models correctly predict the structures of many transition metal complexes, they are by themselves unable to account for several of their special properties:
- The metal-to-ligand bonds are generally much weaker than ordinary covalent bonds;
- Some complexes utilize “inner” d orbitals of the central ion, while others are “outer-orbital” complexes;
- Transition metal ions tend to be intensely colored.
Paramagnetism of coordination complexes
Unpaired electrons act as tiny magnets; if a substance that contains unpaired electrons is placed near an external magnet, it will undergo an attraction that tends to draw it into the field. Such substances are said to be paramagnetic, and the degree of paramagnetism is directly proportional to the number of unpaired electrons in the molecule. Magnetic studies have played an especially prominent role in determining how electrons are distributed among the various orbitals in transition metal complexes.
Studies of this kind are carried out by placing a sample consisting of a solution of the complex between the poles of an electromagnet. The sample is suspended from the arm of a sensitive balance, and the change in apparent weight is measured with the magnet turned on and off. An increase in the weight when the magnet is turned on indicates that the sample is attracted to the magnet (paramagnetism) and must therefore possess one or more unpaired electrons. The precise number can be determined by calibrating the system with a substance whose electron configuration is known.
Supplemental (Optional) Background Reading: Crystal field theory
The current model of bonding in coordination complexes developed gradually between 1930-1950. In its initial stages, the model was a purely electrostatic one known as crystal field theory which treats the ligand ions as simple point charges that interact with the five atomic d orbitals of the central ion. It is this theory which we describe below.
It is remarkable that this rather primitive model, quite innocent of quantum mechanics, has worked so well. However, an improved and more complete model that incorporates molecular orbital theory is known as ligand field theory. In an isolated transition metal atom the five outermost d orbitals all have the same energy which depends solely on the spherically symmetric electric field due to the nuclear charge and the other electrons of the atom. Suppose now that this atom is made into a cation and is placed in solution, where it forms a hydrated species in which six H2O molecules are coordinated to the central ion in an octahedralarrangement. An example of such an ion might be hexaaquotitanium(III), Ti(H2O)63+.
The ligands (H2O in this example) are bound to the central ion by electron pairs contributed by each ligand. Because the six ligands are located at the corners of an octahedron centered around the metal ion, these electron pairs are equivalent to clouds of negative charge that are directed from near the central ion out toward the corners of the octahedron. We will call this an octahedral electric field, or the ligand field.
d-orbital splitting
The differing shapes of the five kinds of d orbitals cause them to interact differently with the electric fields created by the coordinated ligands. This diagram (from a Purdue U. chemistry site) shows outlines of five kinds of d orbitals.
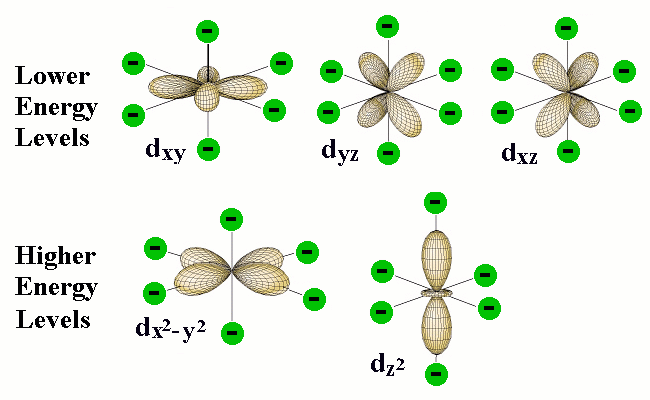
The green circles represent the coordinating electron-pairs of the ligands located at the six corners of the octahedron around the central atom. The two d orbitals at the bottom have regions of high electron density pointing directly toward the ligand orbitals; the resulting electron-electron repulsion raises the energy of these d orbitals.
Although the five d orbitals of the central atom all have the same energy in a spherically symmetric field, their energies will not all be the same in the octahedral field imposed by the presence of the ligands. The reason for this is apparent when we consider the different geometrical properties of the five d orbitals. Two of the d orbitals, designated dx2 and dx2-y2, have their electron clouds pointing directly toward ligand atoms. We would expect that any electrons that occupy these orbitals would be subject to repulsion by the electron pairs that bind the ligands that are situated at corresponding corners of the octahedron. As a consequence, the energies of these two d orbitals will be raised in relation to the three other d orbitals whose lobes are not directed toward the octahedral positions.
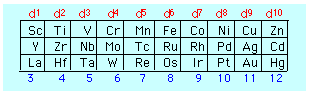
The number of electrons in the d orbital of the central atom is easily determined from the location of the element in the periodic table, taking in account, of course, of the number of electrons removed in order to form the positive ion.
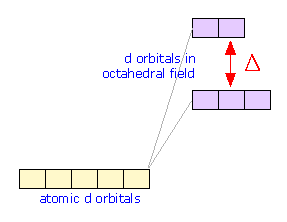
The effect of the octahedral ligand field due to the ligand electron pairs is to split the d orbitals into two sets whose energies differ by a quantity denoted by Δ ("delta") which is known as the d orbital splitting energy. Note that both sets of central-ion d orbitals are repelled by the ligands and are both raised in energy; the upper set is simply raised by a greater amount. Both the total energy shift and Δ are strongly dependent on the particular ligands.
Why are transition metal complexes often highly colored?
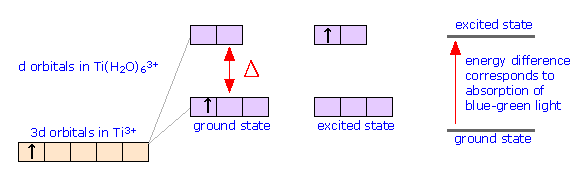
Returning to our example of Ti(H2O)63+, we note that Ti has an outer configuration of 4s23d2, so that Ti3+ will be a d1 ion. This means that in its ground state, one electron will occupy the lower group of d orbitals, and the upper group will be empty. The d-orbital splitting in this case is 240 kJ per mole which corresponds to light of blue-green color; absorption of this light promotes the electron to the upper set of d orbitals, which represents the exited state of the complex. If we illuminate a solution of Ti(H2O)63+ with white light, the blue-green light is absorbed and the solution appears violet in color.
.gif?revision=1&size=bestfit&width=582&height=175)
_complexes_in_aqueous_solution.jpg?revision=1&size=bestfit&width=400&height=130)
High- and low spin complexes
The magnitude of the d orbital splitting depends strongly on the nature of the ligand and in particular on how strong an electrostatic field is produced by its electron pair bond to the central ion.
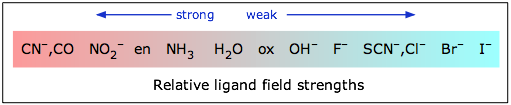
If Δ is not too large then the electrons that occupy the d orbitals do so with their spins unpaired until a d5 configuration is reached, just as occurs in the normal Aufbau sequence for atomic electron configurations. Thus a weak-field ligand such as H2O leads to a “high spin” complex with Fe(II).
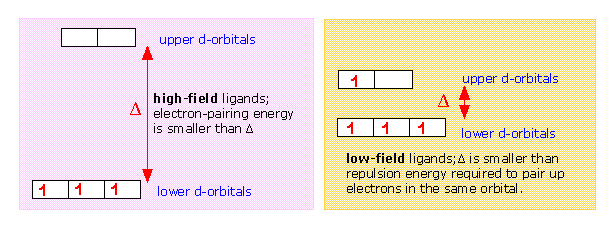
In contrast to this, the cyanide ion acts as a strong-field ligand; the d orbital splitting is so great that it is energetically more favorable for the electrons to pair up in the lower group of d orbitals rather than to enter the upper group with unpaired spins. Thus hexacyanoiron(II) is a “low spin” complex— actually zero spin, in this particular case.
Different d orbital splitting patterns occur in square planar and tetrahedral coordination geometries, so a very large number of arrangements are possible. In most complexes the value of Δ corresponds to the absorption of visible light, accounting for the colored nature of many such compounds in solution and in solids such as \(\ce{CuSO4·5H2O}\) ()Figure \(\PageIndex{1}\).
Coordination Complexes in Biochemistry
Approximately one-third of the chemical elements are present in living organisms. Many of these are metallic ions whose function within the cell depends on the formation of d-orbital coordination complexes with small molecules such as porphyrins (see below). These complexes are themselves bound within proteins (metalloproteins) which provide a local environment that is essential for their function, which is either to transport or store diatomic molecule (oxygen or nitric oxide), to transfer electrons in oxidation-reduction processes, or to catalyze a chemical reaction. The most common of these utilize complexes of Fe and Mg, but other micronutrient metals including Cu, Mn, Mo, Ni, Se, and Zn are also important.
Hemoglobin
Hemoglobin is one of a group of heme proteins that includes myoglobin, cytochrome-c, and catalase. Hemoglobin performs the essential task of transporting dioxygen molecules from the lungs to the tissues in which it is used to oxidize glucose, this oxidation serving as the source of energy required for cellular metabolic processes.
Hemoglobin consists of four globin protein subunits (depicted by different colors in this diagram) joined together by weak intermolecular forces. Each of these subunits contains, buried within it, a molecule of heme, which serves as the active site of oxygen transport. The presence of hemoglobin increases the oxygen carrying capacity of 1 liter of blood from 5 to 250 ml. Hemoglobin is also involved in blood pH regulation and CO2 transport.
Heme itself consists of an iron atom coordinated to a tetradentate porphyrin. When in the ferrous (Fe2+ state) the iron binds to oxygen and is converted into Fe3+. Because a bare heme molecule would become oxidized by the oxygen without binding to it, the adduct must be stabilized by the surrounding globin protein. In this environment, the iron becomes octahedrally-coordinated through binding to a component of the protein in a fifth position, and in the sixth position either by an oxygen molecule or by a water molecule, depending on whether the hemoglobin is in its oxygenated state (in arteries) or deoxygenated state (in veins).
The heme molecule (purple) is enfolded within the polypeptide chain as shown here. The complete hemoglobin molecule contains four of these subunits, and all four must be present for it to function. The binding of O2 to heme in hemoglobin is not a simple chemical equilibrium; the binding efficiency is regulated by the concentrations of H+, CO2, and organic phosphates. It is remarkable that the binding sites for these substances are on the outer parts of the globin units, far removed from the heme. The mechanism of this exquisite molecular-remote-control arises from the fact that the Fe2+ion is too large to fit inside the porphyrin, so it sits slightly out of the porphyrin plane. This Fe radius diminishes when it is oxygenated, allowing it to move into the plane. In doing so, it pulls the protein component to which it is bound with it, triggering a sequence of structural changes that extend throughout the protein.
Myoglobin is another important heme protein that is found in muscles. Unlike hemoglobin, which consists of four protein subunits, myoglobin is made up of only one unit. Its principal function is to act as an oxygen storage reservoir, enabling vigorous muscle activity at a rate that could not be sustained by delivery of oxygen through the bloodstream. Myoglobin is responsible for the red color of meat. Cooking of meat releases the O2 and oxidizes the iron to the +3 state, changing the color to brown.
Carbon monoxide poisoning
Other ligands, notably cyanide ion and carbon monoxide, are able to bind to hemoglobin much more strongly than does iron, thereby displacing it and rendering hemoglobin unable to transport oxygen. Air containing as little as 1 percent CO will convert hemoglobin to carboxyhemoglobin in a few hours, leading to loss of consciousness and death. Even small amounts of carbon monoxide can lead to substantial reductions in the availability of oxygen. The 400-ppm concentration of CO in cigarette smoke will tie up about 6% of the hemoglobin in heavy smokers; the increased stress this places on the heart as it works harder to compensate for the oxygen deficit is believed to be one reason why smokers are at higher risk for heart attacks. CO binds to hemoglobin 200 times more tightly than does \(O_2\).
Chlorophyll
Chlorophyll is the light-harvesting pigment present in green plants. Its name comes from the Greek word χλορος (chloros), meaning “green”- the same root from which chlorine gets its name. Chlorophyll consists of a ring-shaped tetradentate ligand known as a porphin coordinated to a central magnesium ion. A histidine residue from one of several types of associated proteins forms a fifth coordinate bond to the Mg atom.
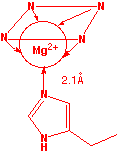
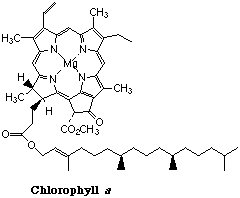
The light energy trapped by chlorophyll is utilized to drive a sequence of reactions whose net effect is to bring about the reduction of CO2 to glucose (C6H12O6) in a process known as photosynthesis which serves as the fuel for all life processes in both plants and animals.


