When analyzing resistor-inductor-capacitor circuits, remember that capacitor voltage cannot change instantaneously, thus, initially, capacitors behave as a short circuit. Once the capacitor has been charged and is in a steady-state condition, it behaves like an open. This is opposite of the inductor. As we have seen, initially an inductor behaves like an open, but once steady-state is reached, it behaves like a short. For example, in the circuit of Figure 9.4.1
, initially \(L\) is open and \(C\) is a short, leaving us with \(R_1\) and \(R_2\) in series with the source, \(E\). At steady-state, \(L\) shorts out both \(C\) and \(R_2\), leaving all of \(E\) to drop across \(R_1\). For improved accuracy, replace the inductor with an ideal inductance in series with the corresponding \(R_{coil}\) value. Similarly, practical capacitors can be thought of as an ideal capacitance in parallel with a very large (leakage) resistance.
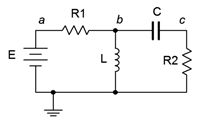
Figure 9.4.1
: Basic RLC circuit.
Assuming the initial current through the inductor is zero and the capacitor is uncharged in the circuit of Figure 9.4.2
, determine the current through the 2 k\(\Omega\) resistor when power is applied and after the circuit has reached steady-state. Draw each of the equivalent circuits.
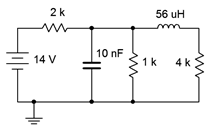
Figure 9.4.2
: Circuit for Example 9.4.1
.
For the initial-state equivalent we open the inductor and short the capacitor. The new equivalent is shown in Figure 9.4.3
. The shorted capacitor removes everything to its right from the circuit. All that's left is the source and the 2 k\(\Omega\) resistor.
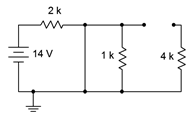
Figure 9.4.3
: Initial-state equivalent of the circuit of Figure 9.4.2
.
We can find the current through the 2 k\(\Omega\) resistor using Ohm's law.
\[I_{2k} = \frac{E}{R} \nonumber \]
\[I_{2k} = \frac{14 V}{2k \Omega} \nonumber \]
\[I_{2k} = 7 mA \nonumber \]
Steady-state is redrawn in Figure 9.4.4
, using a short in place of the inductor, and an open for the capacitor. We are left with a resistance of 2 k\(\Omega\) in series with the parallel combination of 1 k\(\Omega\) and 4 k\(\Omega\), or 2.8 k\(\Omega\) in total.
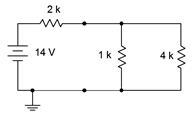
Figure 9.4.4
: Steady-state equivalent of the circuit of Figure 9.4.2
.
\[I_{2k} = \frac{E}{R} \nonumber \]
\[I_{2k} = \frac{14 V}{2.8k \Omega} \nonumber \]
\[I_{2k} = 5mA \nonumber \]






