8.1: Recursion

What is Recursion?
The process in which a function calls itself directly or indirectly is called recursion and the corresponding function is called as recursive function. Using recursive algorithm, certain problems can be solved quite easily. Examples of such problems are Towers of Hanoi (TOH), Inorder/Preorder/Postorder Tree Traversals, DFS of Graph, etc.

What is base condition in recursion?
In the recursive program, the solution to the base case is provided and the solution of the bigger problem is expressed in terms of smaller problems.

int fact(int n)
{
    if (n < = 1) // base case
        return 1;
    else    
        return n*fact(n-1);    
}

In the above example, base case for n < = 1 is defined and larger value of number can be solved by converting to smaller one till base case is reached.

How a particular problem is solved using recursion?
The idea is to represent a problem in terms of one or more smaller problems, and add one or more base conditions that stop the recursion. For example, we compute factorial n if we know factorial of (n-1). The base case for factorial would be n = 0. We return 1 when n = 0.

Why Stack Overflow error occurs in recursion?
If the base case is not reached or not defined, then the stack overflow problem may arise. Let us take an example to understand this.

int fact(int n)
{
    // wrong base case (it may cause
    // stack overflow).
    if (n == 100) 
        return 1;

    else
        return n*fact(n-1);
}

If fact(10) is called, it will call fact(9), fact(8), fact(7) and so on but the number will never reach 100. So, the base case is not reached. If the memory is exhausted by these functions on the stack, it will cause a stack overflow error.

What is the difference between direct and indirect recursion?
A function fun is called direct recursive if it calls the same function fun. A function fun is called indirect recursive if it calls another function say fun_new and fun_new calls fun directly or indirectly. Difference between direct and indirect recursion has been illustrated in Table 1.

// An example of direct recursion
void directRecFun()
{
    // Some code....

    directRecFun();

    // Some code...
}

// An example of indirect recursion
void indirectRecFun1()
{
    // Some code...

    indirectRecFun2();

    // Some code...
}
void indirectRecFun2()
{
    // Some code...

    indirectRecFun1();

    // Some code...
}

What is difference between tailed and non-tailed recursion?
A recursive function is tail recursive when recursive call is the last thing executed by the function. Please refer tail recursion article for details.

How memory is allocated to different function calls in recursion?
When any function is called from main(), the memory is allocated to it on the stack. A recursive function calls itself, the memory for a called function is allocated on top of memory allocated to calling function and different copy of local variables is created for each function call. When the base case is reached, the function returns its value to the function by whom it is called and memory is de-allocated and the process continues.

// A C++ program to demonstrate working of 
// recursion 
#include <bits/stdc++.h> 
using namespace std; 

void printFun(int test) 
{ 
    if (test < 1) 
        return; 
    else { 
        cout << test << " "; 
        printFun(test - 1); // statement 2 
        cout << test << " "; 
        return; 
    } 
} 

int main() 
{ 
    int test = 3; 
    printFun(test); 
    return 0;
} 

Output :

3 2 1 1 2 3

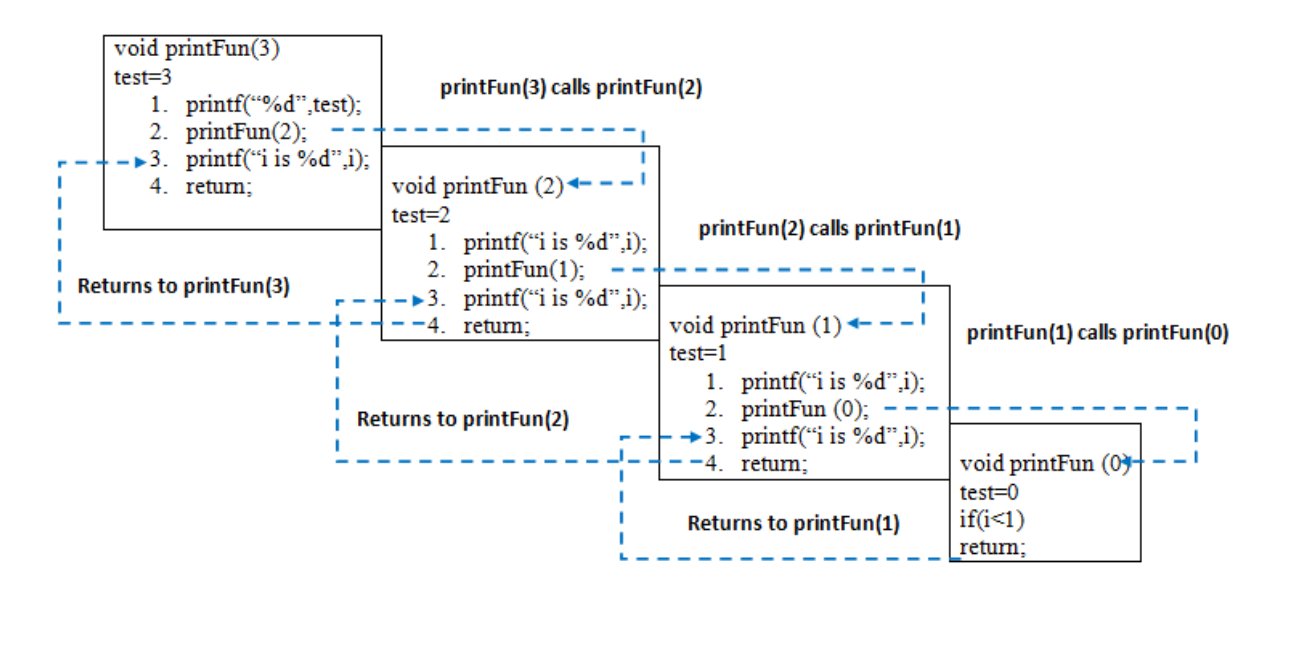
When printFun(3) is called from main(), memory is allocated to printFun(3) and a local variable test is initialized to 3 and statement 1 to 4 are pushed on the stack as shown in below diagram. It first prints ‘3’. In statement 2, printFun(2) is called and memory is allocated to printFun(2) and a local variable test is initialized to 2 and statement 1 to 4 are pushed in the stack. Similarly, printFun(2) calls printFun(1) and printFun(1) calls printFun(0). printFun(0) goes to if statement and it return to printFun(1). Remaining statements of printFun(1) are executed and it returns to printFun(2) and so on. In the output, value from 3 to 1 are printed and then 1 to 3 are printed. The memory stack has been shown in below diagram.

 

 

Below is a example of recursion. In this example the code performs a factorial. In mathematics, the factorial of a positive integer n, denoted by n!, is the product of all positive integers less than or equal to n:

For example,

The value of 0! is 1, according to the convention for an empty product.

// Code to implement factorial 
#include <iostream> 
using namespace std;
// Factorial function 
int factorial(int n) 
{ 
    // Stop condition 
    if (n == 0 || n == 1) 
        return 1; 
    // Recursive condition 
    else
        // we recursively call the factorial function
        // UNTIL n is 0 OR 1...in which case we return 1
        return n * factorial(n - 1); 
} 

// Driver method 
int main() 
{ 
    int n = 5; 
    cout << "Factorial of " << n << " is: " << factorial(n) << endl; 
        return 0; 
} 

Output:

factorial of 5 is: 120

Working: (Read the text on the right from the BOTTOM UP

 

Finally - multiplying 5 by the returned value of 24....giving us the answer of 120 which is returned to main()
↑
Then multiply 4 by the value returned giving us 24
↑
Then it return 2, multiplied by 3, which returns 6
↑
We call the factorial() function until we hit 0 or 1 in which case we return 1.

 

Adapted from:
"Recursion" by Sonal Tuteja, Geeks for Geeks is licensed under CC BY-SA 4.0