9.1: Constraints and Intergrity
- Page ID
- 92183
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Constraints are a very important feature in a relational model. In fact, the relational model supports the well-defined theory of constraints on attributes or tables. Constraints are useful because they allow a designer to specify the semantics of data in the database. Constraints are the rules that force DBMSs to check that data satisfies the semantics.
Domain Integrity
Domain restricts the values of attributes in the relation and is a constraint of the relational model. However, there are real-world semantics for data that cannot be specified if used only with domain constraints. We need more specific ways to state what data values are or are not allowed and which format is suitable for an attribute. For example, the Employee ID (EID) must be unique or the employee Birthdate is in the range [Jan 1, 1950, Jan 1, 2000]. Such information is provided in logical statements called integrity constraints.
There are several kinds of integrity constraints, described below.
Entity integrity
To ensure entity integrity, it is required that every table have a primary key. Neither the PK nor any part of it can contain null values. This is because null values for the primary key mean we cannot identify some rows. For example, in the EMPLOYEE table, Phone cannot be a primary key since some people may not have a telephone.
Referential integrity
Referential integrity requires that a foreign key must have a matching primary key or it must be null. This constraint is specified between two tables (parent and child); it maintains the correspondence between rows in these tables. It means the reference from a row in one table to another table must be valid.
Examples of referential integrity constraint in the Customer/Order database of the Company:
- Customer(CustID, CustName)
- Order(OrderID, CustID, OrderDate)
To ensure that there are no orphan records, we need to enforce referential integrity. An orphan record is one whose foreign key FK value is not found in the corresponding entity – the entity where the PK is located. Recall that a typical join is between a PK and FK.
The referential integrity constraint states that the customer ID (CustID) in the Order table must match a valid CustID in the Customer table. Most relational databases have declarative referential integrity. In other words, when the tables are created the referential integrity constraints are set up.
Here is another example from a Course/Class database:
- Course(CrsCode, DeptCode, Description)
- Class(CrsCode, Section, ClassTime)
The referential integrity constraint states that CrsCode in the Class table must match a valid CrsCode in the Course table. In this situation, it’s not enough that the CrsCode and Section in the Class table make up the PK, we must also enforce referential integrity.
When setting up referential integrity it is important that the PK and FK have the same data types and come from the same domain, otherwise the relational database management system (RDBMS) will not allow the join. RDBMS is a popular database system that is based on the relational model introduced by E. F. Codd of IBM’s San Jose Research Laboratory. Relational database systems are easier to use and understand than other database systems.
Referential integrity in Microsoft Access
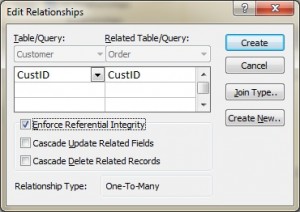
In Microsoft (MS) Access, referential integrity is set up by joining the PK in the Customer table to the CustID in the Order table. See Figure \(\PageIndex{1}\) for a view of how this is done on the Edit Relationships screen in MS Access.
Referential integrity using Transact-SQL (MS SQL Server)
When using Transact-SQL, the referential integrity is set when creating the Order table with the FK. Listed below are the statements showing the FK in the Order table referencing the PK in the Customer table.
CREATE TABLE Customer ( CustID INTEGER PRIMARY KEY, CustName CHAR(35) )
CREATE TABLE Orders ( OrderID INTEGER PRIMARY KEY, CustID INTEGER REFERENCES Customer(CustID), OrderDate DATETIME )
Foreign key rules
Additional foreign key rules may be added when setting referential integrity, such as what to do with the child rows (in the Orders table) when the record with the PK, part of the parent (Customer), is deleted or changed (updated). For example, the Edit Relationships window in MS Access (see Figure 9.1) shows two additional options for FK rules: Cascade Update and Cascade Delete. If these are not selected, the system will prevent the deletion or update of PK values in the parent table (Customer table) if a child record exists. The child record is any record with a matching PK.
In some databases, an additional option exists when selecting the Delete option called Set to Null. In this is chosen, the PK row is deleted, but the FK in the child table is set to NULL. Though this creates an orphan row, it is acceptable.
Enterprise Constraints
Enterprise constraints – sometimes referred to as semantic constraints – are additional rules specified by users or database administrators and can be based on multiple tables.
Here are some examples.
- A class can have a maximum of 30 students.
- A teacher can teach a maximum of four classes per semester.
- An employee cannot take part in more than five projects.
- The salary of an employee cannot exceed the salary of the employee’s manager.

