12.6: Over-Determined Systems of Equations
- Page ID
- 85172
Consistent Equations
Simple examples of consistent over-determined system of equations:
- One equation is a multiple of another equation
- One equation is the of 2 other equations
The rank of a consistent set of equations is equal to the number of unknowns.
"Overdetermined" consistent system: 3 equations, 2 unknowns
x = -1 : 0.2 : 4;
y1 = 5 - 1*x;
y2 = -1 + 2*x;
y3 = 2 + 0.5*x;
The 3 lines intersect in 1 point, so these equations are consistent.
Graphical intersection at (2, 3)

%% Matrix reformulation:
% Put the variables on the left and the constants on the right.
% 1*x + y = 5
% -2*x + y = -1
% -0.5*x + y = 2
% A*xy = B
A = [ 1 1
-2 1
-0.5 1]
B = [ 5
-1
2]
rank(A) % 2
xy = A\B % Matrix algebra solution = (2, 3)
Solution
Add example text here.
.
Over-Determined Consistent System of Equations 1
Over-Determined consistent system of equations of 4 equations in 3 unknowns.
A3 = [3 2 5
4 5 -2
1 1 1
2 -4 -7]
% X3 = [x y z]'
B3 = [22
8
6
-27]
Use Left matrix-division to solve this system of equations for X3
Check your solution by computing this:
X3ck = A3*X3
The result should be close to B3.
- Answer
-
Add texts here. Do not delete this text first.
.
Inconsistent Equations
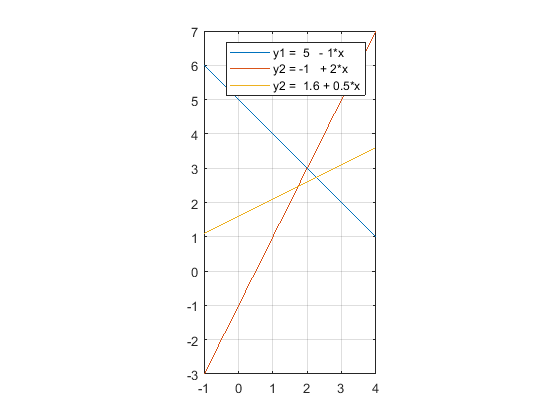
x = -1 : 0.2 : 4;
y1 = 5 - 1*x;
y2 = -1 + 2*x;
y3 = 1.6 + 0.5*x;
% The 3rd equation has been modified, so the 3 lines do not intersect in a single point.
Measurement Errors were added to the right-hand-side values of the consistent version of this exercise. Extra measure ments are often taken to help average-out measurement errors.
These these equations are inconsistent. Rather, there are 3 intersection points of each pair of lines.
%% We can still use left-division (Gaussian elimination)
% to find a good approximate solution.
% Matrix formulation
% 1*x + y = 5
% -2*x + y = -1
% -0.5*x + y = 1.6]
% xy = [x
% y]
% A*xy = B]
A = [ 1 1
-2 1
-0.5 1]
B = [ 5
-1
1.6]
rank(A) % 2
xy = A\B % Solution = (2, 2.87)
Solution
Add example text here.
.
Over-Determined Inconsistent System of Equations 2
Over-Determined inconsistent system of equations of 4 equations in 3 unknowns.
Measurement Errors were added to the right-hand-side values of the consistent version of this exercise. Extra measure ments are often taken to help average-out measurement errors.
A4 = [3 2 5
4 5 -2
1 1 1
2 -4 -7]
% X4 = [x y z]'
B4 = [22+1
8-0.5
6+1
-27-1]
Use Left matrix-division to solve this system of equations for X4
Check your solution by computing this:
X4ck = A4*X4
The result should be somewhat close to B4, but will not match because these equations are inconsistent.
- Answer
-
Add texts here. Do not delete this text first.
.


