14.1: scatter, scatter3
- Page ID
- 85204
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The plot() and scatter() functions can make similar 2D plots
%% Create random x and y data points
n = 20;
x = rand(1, n); % a 1xn vector of random values between 0 and 1
y = rand(1, n); % another 1xn vector of random values between 0 and 1
Compare the results of these codes.
%% Plot with the plot function, open circles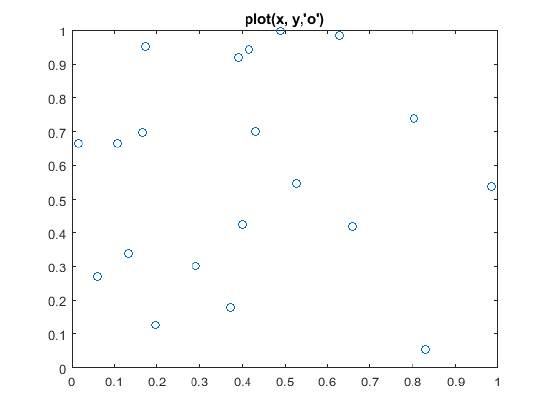
figure;
plot(x, y,'o')
grid on
Figure \(\PageIndex{1}\): plot(x, y,'o')
%% Plot with the scatter function, open circles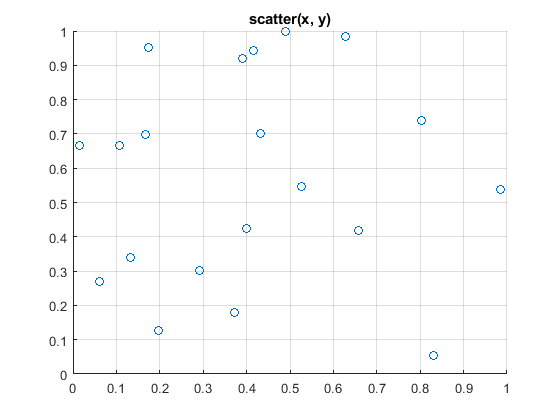
figure;
scatter(x, y)
grid on
Figure \(\PageIndex{2}\): scatter(x, y)
The markers can be filled in and the size changed with both plot() and scatter(), but the options are specified differently:
%% Plot with the plot function, large, filled circles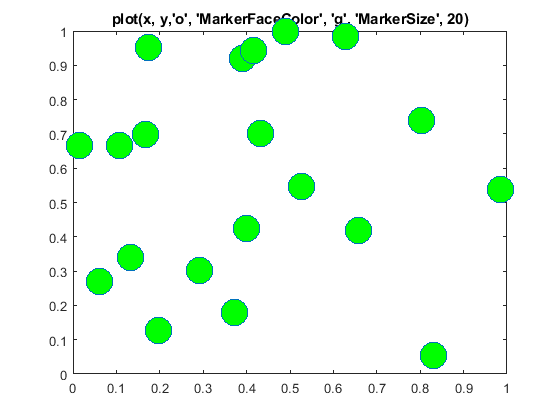
figure;
plot(x, y, 'o', 'MarkerFaceColor', 'g', 'MarkerSize', 20)
title('plot(x, y,''o'', ''MarkerFaceColor'', ''g'', ''MarkerSize'', 20)')
Figure \(\PageIndex{3}\): plot() with MarkerFaceColor and MarkerSize options
%% Plot with the scatter function, large, filled circles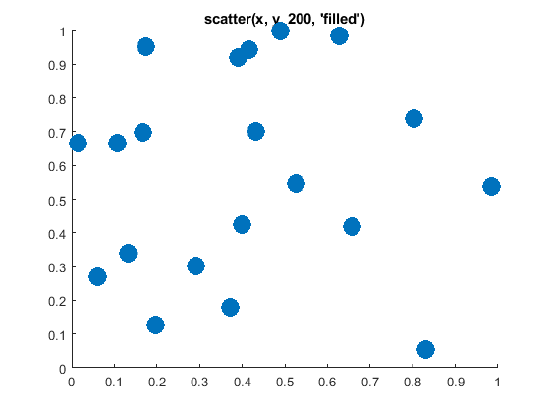
figure;
scatter(x, y, 200, 'filled') % size = 20, filled markers
title('scatter(x, y, 200, ''filled'')')
Figure \(\PageIndex{4}\): scatter() with size and 'filled' options
Solution
Add example text here.
.
This shows the use of the xlim() and ylim() functions with a 2D plot of a curve. It also shows how to use the text() function to add information to a figure. The code is attached in the file xlim_ylim_example.m
%% Example for xlim, ylim, axis
format short g; format compact; close all; clear all; clc;
x = -6:0.1:6;
y = -1 -5*x -0*x.^2 +0.3*x.^3;
figure;
plot(x,y, 'LineWidth',4);
grid on;
title('y = -1 -5*x -0*x^2 +0.3*x^3')
%% Zoom in on x
xlim([-3, 4]) % [x_lower_limit, x_upper_limit]
%% Zoom out in y
ylim([-1, 1]*12) % [y_lower_limit, y_upper_limit]
%% Look for the zero crossing by zooming in on both x & y in 1 command
axis([-1 1 -1 1]*0.5)
% [x_low, x_up, y_low, y_up, ]
% y = 0 at about x = -0.2
%% Check
y_len = length(x) % 121
y(51:60)
% W can see the the closest value to 0 is:
y(59) % -0.0024
% The corresponding x value is:
x(59) % -0.2
axis([-0.3 0.1 -.1 .1]) % zoom in
%% text() example
axis auto % reset the axes to their original scaling
axis('auto')
text(x(59), 0, ['a zero near ',num2str(x(59))])
%% We see that the text is ovelapping with the curve.
% So replot the curve on a new figure and raise the position of the text.
figure;
plot(x,y,'g','LineWidth',2);
grid on;
title('y = -1 -5*x -0*x.^2 +0.3*x.^3')
text(x(59), 2.0, ['a zero near x= ',num2str(x(59))])
%% Put texts near the other zeros
text(-4, 10, ['a zero near x= ',num2str(-4)])
text(4.2, -5, ['a zero near'])
text(4.2, -8, ['x= +4'])
%% Plot arrows pointing to the zeros
hold on;
quiver(-4,10, 0,-10, 'LineWidth',2)
%quiver(x,y, dx,dy)
quiver(4.2,-5, 0,5, 'LineWidth',2)
%quiver(x,y, dx,dy)
Solution
Add example text here.
.
A. Open a new figure and plot these 2 functions on it:
x = (0:0.05:1)*pi;
y1 = 0.3*x;
y2 = cos(2*x);
figure(1)
plot(x,y1)
hold on;
plot(x,y2)
grid on;
We can see that these functions intersect near x = 0.7 and y = 0.2
B. Use xlim, ylim to zoom in on the area near (0.7, 0.2).
Set the x-limits to be [0.5, 1.0]
Set the y-limits to be [0.1, 0.3]
Save the figure and submit it.
The figure can be saved in 2 ways:
1. Under the File menu, select "Save as" and file type *.png or *.jpg and give it a file name.
2. Under the Edit menu, select "Copy Figure", then paste it into a file. This is convenient when writing a report with multiple figures.
- Answer
-
The answer is not given here.
.
[x, y, z] = sphere(16); % 17 x 17 grid
x_size = size(x)
% For the scatter functions, the x, y, and z data need to be 1D
x1 = x(:);
y1 = y(:);
z1 = z(:);
x1_size = size(x1)
%% B. Open a new figure
figure
% Use the scatter() function to make
% a 2D scatter plot of the x & y coordinates
scatter( x, y, 'k','+');
% In Octave, the marker symbol and color are specified separately.
grid on
axis equal % Set the x & y scales to be the same
axis tight % Bring in the x and y axis limits
Solution
.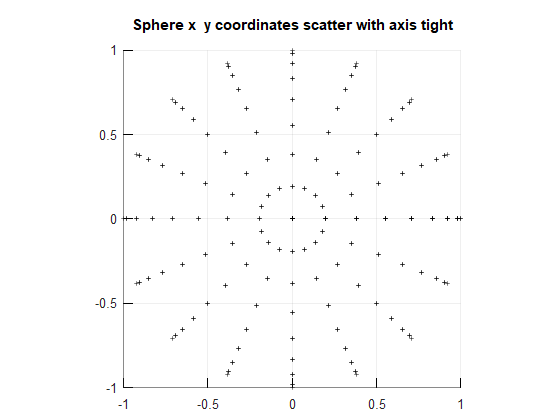
Figure \(\PageIndex{5}\): Sphere scatter 2D
.
The scatter3() function makes 3D plots
%% scatter_plots_sphere.m
format compact; format short; clear all; clc; close all;
% scatter3() can plot data that is not on a rectangular grid.
%% This example is adapted from Matlab's scatter help page.
% sphere() is a built-in example
[X,Y,Z] = sphere(16); % 17 x 17 grid
X1D = X(:); % Convert X from a 17x17 array to a 289x1 vector
Y1D = Y(:); % Convert Y from a 17x17 array to a 289x1 vector
Z1D = Z(:); % Convert Z from a 17x17 array to a 289x1 vector
%% Use scatter3() to create 3D plots.
figure
scatter3(X1D, Y1D, Z1D,'go','filled')
% 'go' = green circles for the data markers
% 'filled' = fills-in the circles
title('3D scatter plot example: sphere')
xlabel('X')
ylabel('Y')
zlabel('Z')
axis equal
%% The view angle can be changed
[az, el] = view % This is the current view angle
% az = -37.5000
% el = 30
view(45,10) % view(azimuth, elevation)
%% Try adjusting the axis limits by evaluating each of these lines, 1 at a time.
xlim([-2,2])
ylim([0,1])
zlim([0,1])
xlim([-1,1])
view(70,30)
view(10,10)
Solution
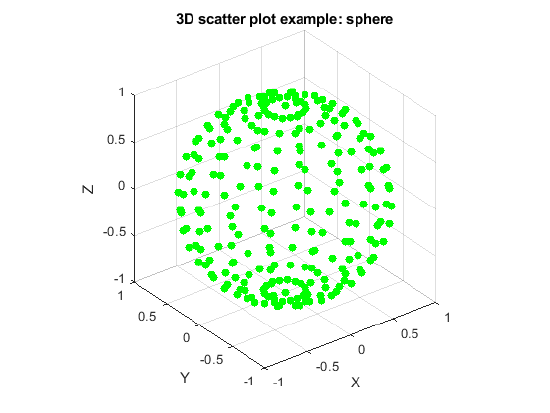
Figure \(\PageIndex{6}\): Sphere scatter3() default view
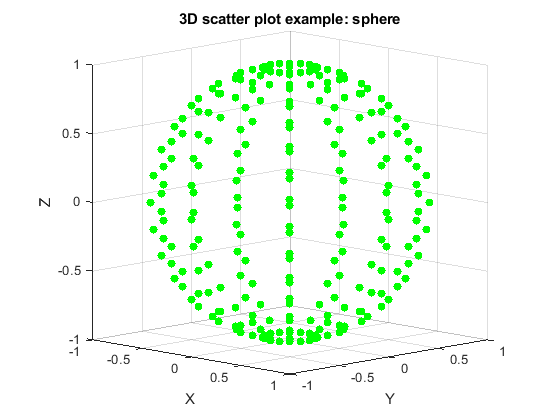
Figure \(\PageIndex{6}\): Sphere scatter3, alternate view
.
.
Next we make a 3-dimensional scatter3() plot.
%% scatter3D_helix.m
format short g; format compact; clear all; close all; clc;
%% The scatter3() function makes a 3D plot of individual points
% The inputs to the scatter3() function are x, y, and z vectors defining each point.
% Unlike other 3D plotting functions, it does not use a 2D grid of x and y coordinates
% Define these x and y vectors:
r = 2; % radius of the helix
ang = 0 : 10 : 3*360; % angles (degs)
x = r*cosd(ang);
y = r*sind(ang);
n = length(ang);
z = (0 : (n-1)) /8;
%% Open a figure and plot this surface using the scatter3() function
% scatter3 expects the 3 inputs to be vectors.
figure;
scatter3(x, y, z);
axis equal
%%
title('scatter3() of a helix');
xlabel('x') % This identifies x-axis
ylabel('y')
zlabel('z')
% You can rotate the graph in 3D.
% You can zoom in.
Solution
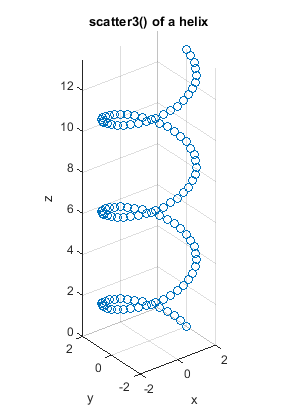
Figure \(\PageIndex{7}\): scatter3 Helix
.
The file scatter3_seamount_start.m code loads the seamount.mat data file. The seamount.mat file is attached to this section. You need to download it. The scatter3_seamount_start.m file and the seamount.mat both need to be in the same directory as the command window.
You need to add the scatter() function to plot the x, y coordinates and the scatter3() function to plot the full 3D seamount. Change the name of the completed .m file scatter3_seamount_YourName.m
- Answer
-
Your figure should look like this:
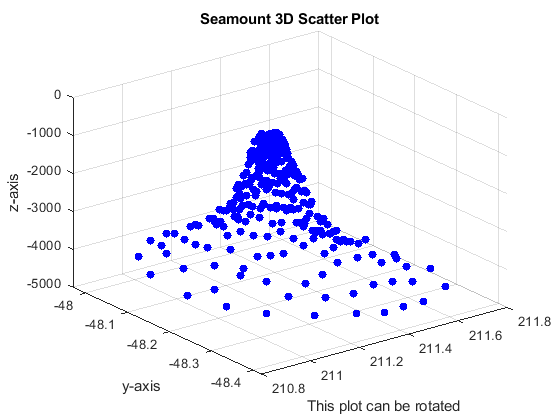
Figure \(\PageIndex{8}\): scatter3 seamount.
.


