18.1: Integration- Computing the Area Under a Curve
- Page ID
- 85387
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This chapter essentially deals with the problem of computing the area under a curve. First, we will employ a basic approach and form trapezoids under a curve. From these trapezoids, we can calculate the total area under a given curve. This method can be tedious and is prone to errors, so in the second half of the chapter, we will utilize a built-in MATLAB function to carry out numerical integration. (This was reformatted by Carey Smith. Also, the text was modified to show integrating a function that is defined in a separate file in addition to showing the use of an anonymous function.)
A Basic Approach
There are various methods to calculating the area under a curve, for example, Rectangle Method, Trapezoidal Rule and Simpson's Rule. The following procedure is a simplified method.
Consider the curve below:
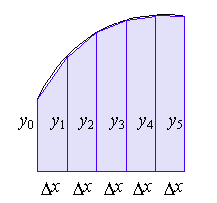
Figure \(\PageIndex{1}\). Numerical integration
Each segment under the curve can be calculated as follows:
\(\frac{1}{2}\left(y_{0}+y_{1}\right) \Delta x+\frac{1}{2}\left(y_{1}+y_{2}\right) \Delta x+\frac{1}{2}\left(y_{2}+y_{3}\right) \Delta x\)
Therefore, if we take the sum of the area of each trapezoid, given the limits, we calculate the total area under a curve. Consider the following example.
Example 1
Given the following data, plot an x-y graph and determine the area under a curve between x=3 and x=30
| Index | x [m] | y [N] |
|---|---|---|
| 1 | 3 | 27.00 |
| 2 | 10 | 14.50 |
| 3 | 15 | 9.40 |
| 4 | 20 | 6.70 |
| 5 | 25 | 5.30 |
| 6 | 30 | 4.50 |
Data Set
First, let us enter the data set.
x=[3,10,15,20,25,30];
y=[27,14.5,9.4,6.7,5.3,4.5];
When you type in [x',y'], you will see the following tabulated result. Here we transpose row vectors with ' and displaying them as columns:
3.0000 27.0000
10.0000 14.5000
15.0000 9.4000
20.0000 6.7000
25.0000 5.3000
30.0000 4.5000
To plot the data type the following:
figure
plot(x,y)
title('Distance-Force Graph')
xlabel('Distance[m]')
ylabel('Force[N]')
grid
The following figure is generated:
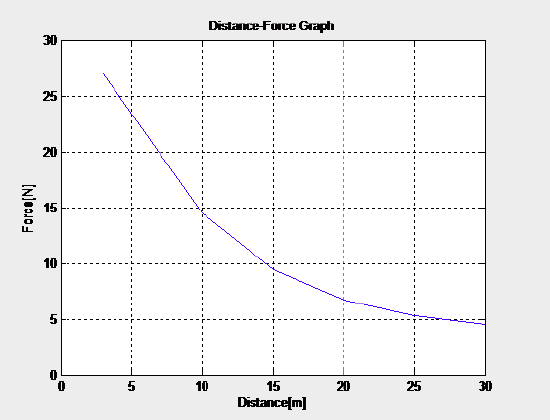
Figure \(\PageIndex{2}\). Distance-Force Graph
To compute dx for consecutive x values, we will use the index for each x value, see the given data in the question.:
dx=[x(2)-x(1)
x(3)-x(2)
x(4)-x(3)
x(5)-x(4)
x(6)-x(5)];
dy is computed by the following command:
dy=[0.5*(y(2)+y(1))
0.5*(y(3)+y(2))
0.5*(y(4)+y(3))
0.5*(y(5)+y(4))
0.5*(y(6)+y(5))];
[dx, dy] % Disply these as a table with 2 columns
7.0000 20.7500
5.0000 11.9500
5.0000 8.0500
5.0000 6.0000
5.0000 4.9000
Our results so far are shown below
| x [m] | y [N] | dx [m] | dy [N] |
|---|---|---|---|
| 3 | 27.00 | ||
| 10 | 14.50 | 7.00 | 20.75 |
| 15 | 9.40 | 5.00 | 11.95 |
| 20 | 6.70 | 5.00 | 8.05 |
| 25 | 5.30 | 5.00 | 6.00 |
| 30 | 4.50 | 5.00 | 4.90 |
x, y and corresponding differential elements
If we multiply dx by dy, we find da for each element under the curve. The differential area da=dx*dy, can be computed using the 'term by term multiplication' technique in MATLAB as follows:
da=dx.*dy
da =
145.2500
59.7500
40.2500
30.0000
24.5000
Each value above represents an element under the curve or the area of trapezoid.
By taking the sum of array elements, we find the total area under the curve.
sum_da = sum(da) % 299.75
The following illustrates all the steps and results of our MATLAB computation.
| x [m] | y [N] | dx [m] | dy [N] | dA [Nm] |
| 3 | 27.00 | |||
| 10 | 14.50 | 7.00 | 20.75 | 145.25 |
| 15 | 9.40 | 5.00 | 11.95 | 59.75 |
| 20 | 6.70 | 5.00 | 8.05 | 40.25 |
| 25 | 5.30 | 5.00 | 6.00 | 30.00 |
| 30 | 4.50 | 5.00 | 4.90 | 24.50 |
| 299.75 |
Computation of the approximate area under a curve
The Trapezoidal Rule
Sometimes it is rather convenient to use a numerical approach to solve a definite integral. The trapezoid rule allows us to approximate a definite integral using trapezoids.
The trapz() Function
Z = trapz(Y) computes an approximation of the integral of Y using the trapezoidal method.
Now, let us see a typical problem.
Example 2
Given Area \(=\int_{2}^{5} x^{2} d x\), an analytical solution would produce 39.
Use trapz command and solve it
Initialize variable x as a row vector, from 2 with increments of 0.1 to 5:
x=2:.1:5;
Declare variable y as y=x^2;.
Note the following error prompt: ??? Error using ==> mpower Inputs must be a scalar and a square matrix.
This is because x is a vector quantity and MATLAB is expecting a scalar input for y.
Because of that, we need to compute y as a vector and to do that we will use the dot operator as follows: y=x.^2;.
This tells MATLAB to create vector y by taking each x value and raising its power to 2.
Now we can issue the following command to calculate the first area, the output will be as follows:
area1=trapz(x,y)
area1 =
39.0050
Notice that this numerical value is slightly off. So let us increase the number of increments and calculate the area again:
x=2:.01:5;
y=x.^2;
area2=trapz(x,y)
area2 =
39.0001
Yet another increase in the number of increments:
x=2:.001:5;
y=x.^2;
area3=trapz(x,y)
area3 =
39.0000
Example 3
Determine the value of the following integral:
\(\int_{0}^{\pi} \sin (x) \mathrm{d} x\)
Initialize variable x as a row vector, from 0 with increments of pi/100 to pi:
x=0:pi/100:pi;
Declare variable y as
y=sin(x);
Issue the following command to calculate the first area, the output will be as follows:
area1=trapz(x,y)
area1 =
1.9998
Let us increase the increments, as above:
x=0:pi/1000:pi;
y=sin(x);
area2=trapz(x,y)
area2 =
2.0000
Example 4
A gas expands according to the law, PV1.4=c.
Initially, the pressure is 100 kPa when the volume is 1 m3.
Write a script to compute the work done by the gas in expanding to three times its original volume1.
Recall that PV diagrams can be used to estimate the net work performed by a thermodynamic cycle, see Wikipedia or we can use definite integral to compute the work done (WD) as follows:
\(\mathrm{WD}=\int p \mathrm{d} v\)
If we rearrange the expression pressure as a function of volume, we get:
\(P=\frac{c}{V^{1.4}}\)
By considering the initial state, we can determine the value of c:
\(\begin{aligned} c &=100 \times 1^{1.4} \\ &=100 \end{aligned}\)
From the equation and the equation above, we can write:
\(P=\frac{100}{V^{1.4}}\)
\(\mathrm{WD}=\int_{1}^{3} \frac{100}{v^{1.4}} \mathrm{d} v\)
For MATLAB solution, we will consider P as a function of V and WD. Now, let us apply the three-step approach we have used earlier:
1. Initialize variable volume as a row vector, from 1 with increments of 0.001 to 3:
v=1:0.001:3;
2. Declare variable pressure as
p=100./v.^1.4;
3. Use the trapz function to calculate the work done, the output will be as follows:
WorkDone=trapz(v,p)
WorkDone =
88.9015
These steps can be combined in an m-file as follows:
clc
disp('A gas expands according to the law, pv^1.4=C')
disp('Initial pressure is 100 kPa when the volume is 1 m3')
disp('Compute the work done by the gas in expanding')
disp('To three times its original volume')
disp(' ') % Display blank line
v=1:.001:3; % Creating a row vector for volume, v
p=100./(v.^1.4); % Computing pressure for volume
WorkDone=trapz(v,p) % Integrating p*dv over 1 to 3 cubic meters
Example 5
A body moves from rest under the action of a direct force given by \(F=\frac{15}{x+3}\)
where x is the distance in meters from the starting point. Write a script to compute the total work done in moving a distance 10 m.2
Recall that the general definition of mechanical work is given by the following integral, see Wikipedia:
\(\mathrm{WD}=\int F \mathrm{d} x\)
Therefore we can write:
\(\mathrm{WD}=\int_{0}^{10} \frac{15}{x+3} \mathrm{d} x\)
Applying the steps we followed in the previous examples, we write:
clc
disp('A body moves from rest under the action of a direct force given')
disp('by F=15/(x+3) where x is the distance in meters')
disp('From the starting point.')
disp('Compute the total work done in moving a distance 10 m.')
disp(' ') % Display blank line
x=0:.001:10; % Creating a row vector for distance, x
F=15./(x+3); % Computing Force for x
WorkDone=trapz(x,F) % Integrating F*dx over 0 to 10 meters.
The output of the above code is:
A body moves from rest under the action of a direct force given
by F=15/(x+3) where x is the distance in meters from the starting point.
Compute the total work done in moving a distance 10 m.
WorkDone =
21.9951
The integral() Function
As we have seen earlier, trapz gives a good approximation for definite integrals. The integral function streamlines numerical integration even further.
(Note by Carey Smith: the original version introduces anonymous functions. It is not necessary to use anonymous functions. It is simpler to create a separate function file like was done for the fzero() function in Chapter 10. Another alternative for MATLAB, but not for Octave, is to create a subfunction at the bottom of the script. )
Syntax for integral()
To evaluate an integral from a minimum to a maximum value, we specify a function and its minimum and maximum
Z = integral(@fun, xmin, xmax).
@fun is a function handle to the function that you want to integrate.
xmin is the lower bound of the integral and xmax is th eupper bound of the integral.
Example 6
Given y=x^2, evaluate the integral from x=2 to x=5 as we have done it with trapz command.
Define a function called "myfunction.m"
function y = myfunction(x)
y = x.^2;
end
Test integrating this function from x = 2 to 5 with this code:
Z = integral(@myfunction, 2, 5)
You should get a result of Z = 39.
Notice that, unlike in the examples, we did not need to define a vector and change the increments to get an accurate result.
The integral() function determines appropriate point spacings. Typically, the spacing will not be uniform, but are optimized for speed an accuracy.
.
Anonymous Functions (Optional)
An anonymous function is a function that can be defined in the command window (i.e. it does not need to be stored in a program file). Anonymous functions can accept inputs and return outputs, just as standard functions do such as sqrt(X) or log(X).
To define an anonymous function, first we create a handle with @(x) and type in the function:
myfunction=@(x) x^2+1.
If you want to evaluate myfunction at 1, just type in a=myfunction(1) at the command window and you get the result of 2.
.
Summary of Key Points
- In its simplest form, numerical integration involves calculating the areas of segments that make up the area under a curve,
- MATLAB has built-in functions to perform numerical integration,
Z = trapz(Y)computes an approximation of the integral of Y using the trapezoidal method.- Anonymous functions are inline statements that we can define with
@(x), Z = integral(fun,xmin,xmax)numerically integrates functionfunfromxmintoxmax.


