3.4.2: Entropy

The First Law was an easy part. But in order to explain what the Second Law talks about, we have to introduce the notion of Entropy.

Entropy is widely regarded as one of the most difficult concepts in academic physics curriculum. It's a parameter that characterizes the state of a thermal system. Other state parameters are the internal energy \(U\), volume \(V\), the amount of substance (usually expressed as the number of moles \(N\) a mole consists of \(6.022 \times 10^{23}\) molecules \(^{1}\) of a given substance). Furthermore, the temperature \(T\), and the pressure \(p\). They are all "intuitively clear", right? In contrast, entropy, conventionally denoted as \(S\), is an abstract function.

It's mathematically defined, and the definition is not very complicated. Namely, if a portion of heat \(\Delta Q\) is transferred in or out of a body of temperature \(T\) (either an individual body, or a body being a part of a larger system, otherwise isolated) the change \(\Delta S\) in the body's/system's entropy is:

\[ \Delta S=\frac{\Delta Q}{T} \]

So, by adding heat one can increase the entropy of a system, and by removing heat e.g., through contact with a cooler body one can lower the systems entropy.

An Example. Perhaps a good thing to do now would be to discuss a simple example. OK, consider a \(1 \mathrm{~kg}\) sample of ordinary water, \(\mathrm{H}_{2} \mathrm{O}\). At very low temperature it's a solid piece of ice. If we start adding heat to it by small portions \(\Delta Q\), each time its entropy will grow by \(\Delta S=\Delta Q / T\), according to the Equation 3.7. But when we add heat, we also add energy, right? So, after each step, the temperature will also grow a bit.

As the process continues, the temperature will gradually increase, as illustrated in the Fig. \(3.6\) - until it reaches the ice melting point \(T_{f}=273 \mathrm{~K}\). In order to melt a mass unit of ice, one has to add an amount of heat called the heat of fusion, equal \(334 \mathrm{~kJ} / \mathrm{kg}\), or \(6.01 \mathrm{~kJ}\) per one mole of water (the mass of one mole of \(\mathrm{H} 2 \mathrm{O}\) is \(18.01528 \mathrm{~g}\) ).

Figure \(\PageIndex{1}\): The change of entropy of one mole of water, when heat is grad- ually added by small portions, starting from a very low temperature. When the ice melting point is reached (273 K), the temperature does not change until all ice melts down – which produces the vertical “step” on the curve. Another such “step” occurs at water boiling temperature – again, the tem- perature of 373 K does not change as long as all water “boils off” – this transition require adding 6.75 times more heat than in the case of ice melt- ing, therefore the “step” is considerably higher.

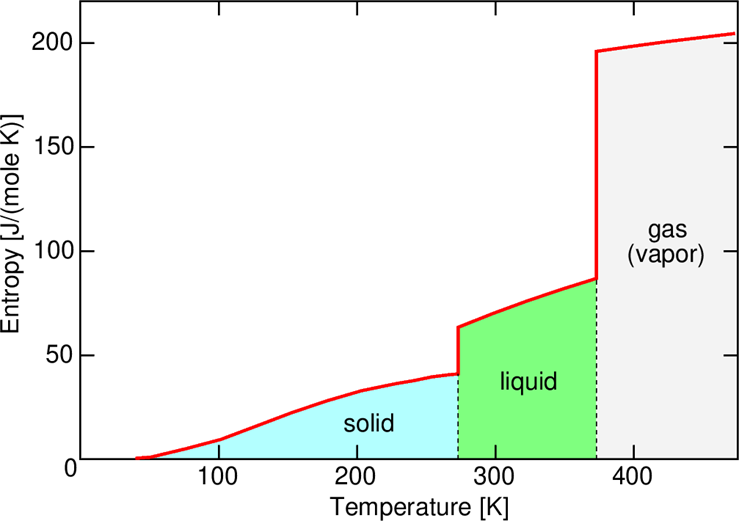
Now, the temperature stops growing, until the small portions \(\Delta Q\) add up to \(334 \mathrm{~kJ}\) (for a \(1 \mathrm{~kg}\) sample) or \(6.01 \mathrm{~kJ}\) for a single mole. But the entropy keeps growing during the process, as shown by the vertical part of the curve in the Fig. 3.6. During the entire melting process, it increases by \(334 \mathrm{~kJ} / 273 \mathrm{~K}=1.22 \mathrm{~kJ} / \mathrm{K}\) (or by \(6.01 \mathrm{~kJ} / 273 \mathrm{~K}=22.01 \mathrm{~J} / \mathrm{K}\) for one mole). After all ice changes to water, the temperature starts increasing again, until it reaches the boiling temperature \(T \mathrm{~b}=373 \mathrm{~K}\). Again, the temperature stops growing, because in order to change one kg of liquid water to water vapor, the energy of \(2256 \mathrm{~kJ}\) is needed (or \(40.68 \mathrm{~kJ}\) per one mole). So, again the temperature stops growing, until all small portions \(\Delta Q\) add up to this value - but the entropy in the course of this process increases by \(2256 \mathrm{~kJ} / 373 \mathrm{~K}=\) \(6.05 \mathrm{~kJ} / \mathrm{K}\) per one kilogram (or by \(40.68 \mathrm{~kJ} / 373 \mathrm{~K}=109.06 \mathrm{~J} / \mathrm{K}\) for one mole), creating another "vertical jump" on the curve, much higher than that at \(273 \mathrm{~K}\). After that, the temperature of water, now in gas (vapor) form, will again start increasing.

The purpose of the above example is to show that the value of entropy can be obtained from calculations. In the Web one can find tables and online calculators.

Another example The process of water heating described above is reversible. If we started to take away small portions of heat, we would return to the original state along the same curve. There are, however, processes that cannot be reversed - called irreversible. Consider the following example: there are two \(1 \mathrm{~kg}\) blocks of aluminum, placed into a container that is totally impermeable to heat - no heat can flow in or flow out. The blocks initially do not touch one another. The temperature of one of them (Block 1) is \(T_{1}\), and of the other (Block 2) is \(T_{2}\), with \(T_{1}>T_{2}\).
The relation between the amount of heat \(\Delta Q\) that flows in or out of aluminum, and the change \(\Delta T\) of its temperature is caused by the process is:

\[ \Delta Q=C_{\mathrm{Al}} \Delta T \text { or } \Delta T=\frac{\Delta Q}{C_{\mathrm{Al}}} \]

where \(C_{\mathrm{Al}}\) is a "material constant" called heat capacity. For Aluminum, its value is \(900 \mathrm{~J} / \mathrm{kg} \mathrm{K}\).

If we now bring the two blocks together to establish thermal contact between them, heat will start flowing from Block 1 into Block 2 . The process will last until the temperature of both gets equal. Call this temperature \(T_{12}\). An obvious guess is that it is equal to the arithmetic average of \(T_{1}\) and \(T_{2}\), i.e.,

\[ T_{12}=\frac{T_{1}+T_{2}}{2} \]

To check whether it's a right guess, lets calculate the heat transferred out of Block 1 and heat transferred into Block2. The energy conservation law states that they must be equal! OK, let's then see. First, we find the change of the temperature of Block 1. An algorithm for a temperature change \(\Delta T\) is always: the final temperature minus the initial one. So, we get:

\[ \Delta T_{1}=T_{12}-T_{1}=\frac{T_{1}+T_{2}}{2}-T_{1}=-\frac{T_{1}-T_{2}}{2} \]

So that the heat transfer out of Block 1 is, according to the Eq. \(3.8\) : \(\Delta Q_{\text {out of Block } 1}=-C_{\mathrm{Al}} \frac{T_{1}-T_{2}}{2}\)

In a similar fashion, we get:

\[ \Delta T_{2}=T_{12}-T_{2}=\frac{T_{1}+T_{2}}{2}-T_{2}=\frac{T_{1}-T_{2}}{2} \]

and \(\Delta Q_{\text {into Block } 2}=C_{\mathrm{Al}} \frac{T_{1}-T_{2}}{2}\)

So, everything is correct - the same amount flows out of Block 1 (therefore the minus sign) as it flows in Block \(2 .\)

However, let's now see what happens with the entropy. Let's focus on the very beginning of the process, when only a tiny amount of heat \(d Q\) managed to get out of Block 1, and into Block 2. So, the change of entropy of Block 1 is \(d S_{1}=-d Q / T_{1}\) (minus, because dQ flows out of Block 1), and of Block 2 is \(d S_{2}=d Q / T_{2}\). The total change of entropy of the system of two block is the sum of the two:

\[ d S_{\text {tot }}=d S_{1}+d S_{2}=-\frac{d Q}{T_{1}}+\frac{d Q}{T_{2}}=d Q\left[-\frac{1}{T_{1}}+\frac{1}{T_{2}}\right]=d Q\left[\frac{T_{1}-T_{2}}{T_{1} T_{2}}\right] \]

Note that the last right-hand expression in square brackets is a non-zero positive number. What does it mean? It means that the entropy of thetwoblock system increases in the course of the heat transfer process. But not only during the initial short period - the same math remains valid for any moment until the heat stops flowing. So, the conclusion is that this process of heat exchange between the blocks increases the entropy of the two-block system.

The exchange of heat between two bodies is always an irreversible process: the heat flows spontaneously from the warmer to the cooler body, but the opposite may never happen. There are many other types of irreversible thermodynamic processes, and all have one in common: if such processes occur in thermally isolated system (often called adiabatic by professionals), the entropy of the system always increases. Entropy may stay constant only if all processes in an adiabatic system are fully reversible. And the entropy in an adiabatic system can never ever decrease!

_____________________________________________

1Why such an “exotic” number? Well, once it has been decided that a mole of hydrogen, the simplest of all elements, would be the number of hydrogen atoms in a mass unit, a gram (g). And there are \( 6.022 \times 10_{23} \) atoms in a gram of hydrogen – it’s called the Avogadro Number. Then it has been decided that a mole of any other pure substance is the Avogadro Number of molecules of this substance.