4.6.2: No magic tricks are necessary!
- Page ID
- 85098
The “recipe” given above may sound a bit like one of those prescriptions from Harry Potter books – but, in fact, no supernatural powers are needed. As it follows from the result we have obtained in the second Example in Section 1.4, a fission neutron can travel a relatively long way in pure U-238. Natural uranium has only 0.7% of the U-235 isotope, which only marginally changes the cross section we used in the calculations. Accordingly, there is no need to use any tricks for removing the fission neutron from the fuel element: if the fuel is in the form of long rods, half inch or one inch in diameter, most of the fission neutrons will fly out “all by themselves”.
So, the first step of the “recipe” is completed. Now comes the step number two: take away the energy from the fission neutrons. How do we take away kinetic energy from neutrons?
The answer is simple: the only way of doing it without destroying the neutron is by colliding it with atomic nuclei. Some atomic nuclei would gladly “swallow” an impinging neutron, but some have no appetite for them whatsoever and the neutron simply “bounces off” the nucleus. Here the behavior of the two objects shows much analogy to the collision of two billiard balls of different masses.
It may be helpful now to recall the introductory physics problem: a ball of mass m moving with speed v is approaching, on a head-on collision course, another ball of mass M which is at rest (V = 0). Assuming that the collision is perfectly elastic (i.e., both energy and momentum is conserved in the process), find the kinetic energy of each ball after the collision. We will not solve the problem here, but only quote the results. The velocities after the collision are:
\[ v^{\prime}=v \frac{m-M}{m+M} \quad \text { and } \quad V^{\prime}=v \frac{2 m}{m+M} \]
and the kinetic energies:
\[ K_{m}^{\prime}=\frac{m v^{2}}{2}\left(\frac{m-M}{m+M}\right)^{2} \text { and } \quad K_{M}^{\prime}=\frac{M v^{2}}{2}\left(\frac{2 m}{m+M}\right)^{2} \]
The thing of real interest for us is the ratio of the energy \(K_{m}^{t}\) of the \(m\) ball after the collision to that before the collision (\left(K_{m}=\frac{1}{2} m v^{2}\right)\) :
\[ \frac{K_{m}^{\prime}}{K_{m}}=\left(\frac{M-m}{M+m}\right)^{2} \]
There is one reason this simple result from introductory classical mechanics is shown here: namely, from his long experience in teaching the basic reactor physic, the Author knows that the problem of "slowing down" neutrons through collisions can be "counterintuitive". Many times a student, when given the question: What do you thing? What is the more efficient way of slowing down neutrons - in other words, of lowering their kinetic energy - by colliding them with light nuclei, or with heavy nuclei? responded with confidence: With heavy nuclei, I believe! - and was a bit surprised when told that "with light nuclei" was the right answer. Evidently, it's an example of a simple problem which is misleading if one applies physical thinking based exclusively on the so-called "conceptual understanding".
But it is easy to fix such incorrect thinking. Suppose that you throw a golf ball against a bowling ball. The golf ball bounces back, the bowling ball hardly even budges. Now, take a toy called the "Newton's Cradle" in which there are several steel balls suspended from a frame, so that one can study collisions. Use only two balls and see what happens, if one ball hits the other which is at rest: the ball that moved stops, the other takes over its entire kinetic energy.
Indeed, this is exactly what the Eq. \(4.8\) states. Let's check: the golf ball mass is \(1.62\) ounces, and the mass of the bowling ball is 16 pounds, i.e., the latter is 158 times heavier than the former. So, for such a mass proportion we get from the equation we get that the energy of the small ball after the collision is still \((157 / 159)^{2}=97.5 \%\) of that before the collision, so it loses only \(2.5 \%\) of its initial energy.
Now, consider a fission neutron. We want it to get slowed from energy 1.6 \(\mathrm{MeV}\) down to \(0.1 \mathrm{eV}\) - i.e., \(1.6 \times 1 \mathrm{O}^{7}\) times, through a chain of multiple collisions. If in each collision the neutron loses \(2.5 \%\) of its energy, then it needs to collide nearly 700 times \(^{1}\)
In contrast, if the neutron collides with a deuteron, \({ }_{1}^{2} \mathrm{H}\), the mass ratio \(M / m\) is close to 2 , then after a single collision only \((1 / 3)^{2}=1 / 9\) remains, and only 9 successive collisions are needed to reduce the neutron energy from \(1.6 \mathrm{MeV}\) to \(0.1 \mathrm{eV}\). And for Carbon, \({ }_{6}^{12} \mathrm{C}\), it is, respectively \((11 / 13)^{2}=0.715\), and 50 collisions.
In fact, it is not exactly so simple - the Eq. \(4.8\) was derived for the assumption that the collision is central, whereas in the real world not all collisions are central, not always the impinging particle moves exactly along the line connecting the centers of both particles. In non-central collisions neutrons loseless energy than central ones - therefore, the actual number of collisions needed to slow fission neutrons down to \(0.1 \mathrm{eV}\) may be higher by a factor 2-3 than the values obtained above. Anyway, it is true that Deuterium and Carbon are very efficient as "neutron energy reducers". In professional language, the process of slowing neutrons down is called moderation, and the materials used for this purpose are called moderators. Pure Deuterium would be difficult to use because it’s a gas; but an excellent moderator is Deuterium oxide, \(D_{2}O \), which is a liquid known as “heavy water”. The element of Carbon may occur in many different forms – e.g., black sooth, graphene, diamond, and graphite are all pure forms of carbon. But only graphite is used as a neutron moderator.
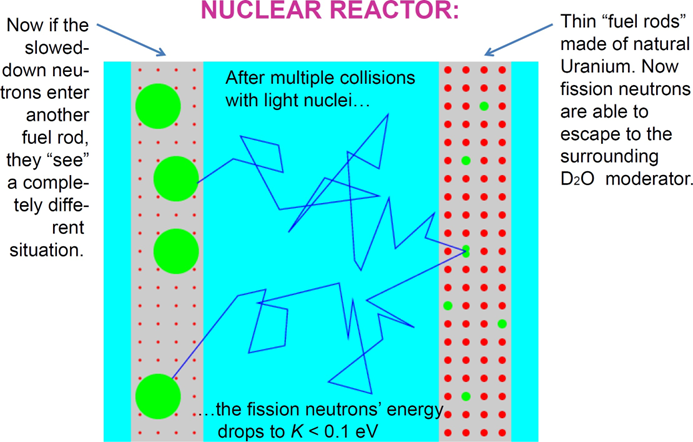
As follows from the above, the uranium fuel rod should be immersed in a tank of heavy water \(D_{2}O \), or put into a block of graphite. Then, the fission neutrons escaping from the rod get slowed down to energies below 0.1 eV.

What should be done next to obtain a controlled chain reaction? If a slow neutron now reenters a fuel rod, it “sees” a completely different situation. The cross section of the fissile U-235 nuclei is now several hundred times larger than that of U-238 nuclei. So, even though the U-235 nuclei are still a 1:140 minority, it is more likely that the neutron will interact with one of them, than with a U-238 nucleus. And trigger another fission, releasing 2-3 new fission neutrons –and the chain reaction will continue!
There is still one small problem – after zig-zagging in the moderator, the neutron may simply escape. How to make sure it re-enters the fuel rod? Well, should it necessarily be the same fuel rod? Of course not, another fuel rod will be as good as the one in which the fission neutron has originated. To increase the probability of re-entering, the uranium fuel in reactors is arranged in the form of a lattice consisting of several hundred, or even of several thousand fuel rods.
___________________________________________________
1. If after the first collision the kinetic energy is \(0.975\) of the initial value, then after the second it is \(0.975 \times 0.975=0.975 \mathbf{2}\). After the third collision it is \(0.975 \mathbf{2} \times 0.975=0.975 \mathbf{s}\), and so on. In order to find the number of collisions that will reduce the energy \(1.6 \times 10 \boldsymbol{7}\) times - in other words, so it is only \(6.25 \times 10^{-}\)of the initial energy - one has to solve the equation \(0.975^{N}=6.25 \times 10^{-}\), which can be readily done using a calculator.

