9.2.1: The Flash Steam Method

Last updated
Save as PDF

Page ID: 85148

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

This method is the most popular one. The lower limit of hot water temperature making it possible to use this technique is given in the literature as 180^◦C. In order to explain how the method works, it’s good to use an example with “real numbers”.

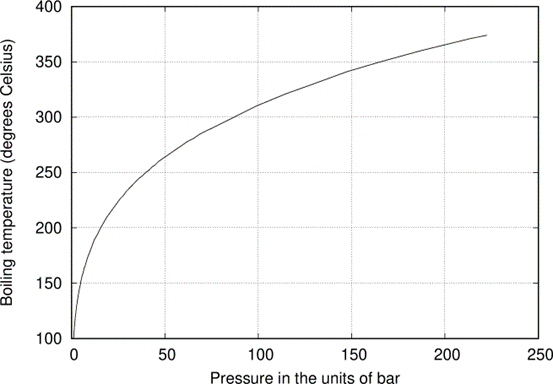
Increasing pressure increases the boiling point of water. The curve is not linear, but increases quicker at low pressures. — Figure \(\PageIndex{1}\): The boiling temperature of water as a function of pressure. It has to be kept in mind that in the process commonly referred to as “boiling”, the liquid phase and the gas phase (steam) of water **coexist** – so that a point (*p, t*) lying on the curve can be interpreted as: *the pressure p needed to keep water liquid at temperature t* (source: aop).

OK, so let’s assume that the water temperature at the outlet of the pro- duction well is 225^◦C. At this temperature, as one can readily find from the graph in Fig. \(\PageIndex{1}\), the pressure needed to keep water in liquid state is 25 bara¹. Now, the 225^◦C water is let to flow into a flash tank, in which the pressure is much lower – say, 10 bara. What happens then? At 10 bar, as we find from the graph in the engineering source linked above, water can stay liquid only if its temperature is no higher than 185^◦C. So, after entering the flash tank it starts to boil violently, until its temperature falls down to 185^◦C. It takes only a split second, hence the term “flash” – and in the process much of the water changes into steam. So, as the result, one obtains water of temperature 185^◦C as well as a generous portion² of steam of 185^◦C temperature and of 10 bara pressure. This steam is sent to a turbine, whereas the 185^◦C water is recirculated down to the heat reservoir.

____________________________________________________________

1The bara is a unit of absolute pressure – it’s not an official unit in the SI system, it’s only “tolerated” by it – but engineers like it. One bara is equal to 100,000 Pascals, where a Pascal (Pa) is an official SI unit of pressure, equal to 1 N/m². The reason why the bara is so popular among engineers is that it is approximately equal to the atmospheric pressure at standard conditions. will spare you the calculation details, but with the help of another table from an Engineer’s Handbook one can find that for the temperature and pressure data used in our example 10.1% of the hot water entering the flash tank changes into steam. For higher

hot water temperature this percentage may increase significantly. It should be noted that steam turbines “like” high-pressure steam. In thermal coal- fired or gas-fired power plants the water is usually heated above the critical point, in order to obtain the so-called superheated steam with a pressure even higher than water’s critical pressure of 220 bara.