9.4.1: Shallow Geothermal Heating

As was discussed in the Chapter describing heat engines, it is the Second Law of Thermodynamics which does not allow us to take advantage of all energy contained by fuels – one is tempted to say that the 2^nd Law “steals” 2/3 or more of the thermal energy one puts into a thermal engine to be converted to mechanical work. Such a theft is outrageous, isn’t it?

Figure \(\PageIndex{1}\): Left image: a Carnot engine – an ideal heat engine converting heat to work with maximum efficiency. Right image: a heat pump – a Carnot engine working in reverse. Work is the input, and now the engine transfers heat from the cold reservoir to the hot reservoir source: aop).

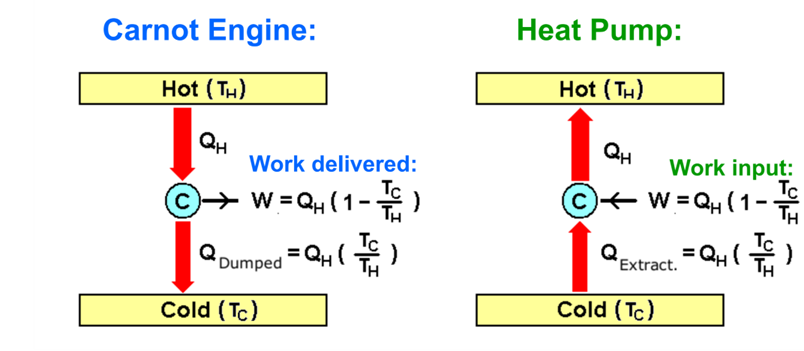
However, it was Lord Kelvin – one of the greatest physicists of the 19^th century – who in 1855 pointed out that in certain situations the 2^nd Law can work in our favor. Namely, not when we convert heat to mechanical work, but – conversely – when we convert mechanical work to heat. Not always – only when we use a machine called the “heat pump”.

Let’s us quickly recall how an ideal heat engine – the Carnot engine – works. Most thermal engines we deal with work in cycles. Let’s analyze what happens in a single cycle. A portion of heat Q_H (we will call it the “heat input") is transferred to the engine from a "hot reservoir" of temperature \(T \mathrm{H}\). It means that at the same time a portion of entropy \(\mathrm{SH}=Q \mathrm{H} / T_{\mathrm{H}}\) "enters" the engine.

Now, the engine converts some of the input heat \(Q \mathrm{H}\) to work \(W\) (we will call it the "work output") - and transfers the remaining heat part Qc to a "heat sink", i.e., to "cold reservoir" of temperature \(T_{\mathrm{C}}\).

From the First Law of Thermodynamics it follows, of course, that:

\[ W=Q_{\mathrm{H}}-Q_{\mathrm{C}} \]

Now the transfer of \(Q_{\mathrm{C}}\) to the cold reservoir of temperature \(T_{\mathrm{C}}\) is associated with a transfer of entropy \({ }^{1} \mathrm{SC}_{\mathrm{C}}=Q_{\mathrm{C}} / T_{\mathrm{C}}\) to this reservoir.

In order to invoke the Second Law, we have to start thinking of the three elements (hot reservoir) + (the engine) + (cold reservoir) as of a single SYSTEM. A portion of entropy \(\mathrm{SH}_{\mathrm{H}}\) is taken out of the hot reservoir, and then a portion \(S_{C}\) is deposited in cold reservoir. Accordingly, the change in the entropy of the SYSTEM is:

\[ \Delta S_{\text {SYSTEM }}=Q_{\mathrm{C}}-Q_{\mathrm{H}} \]

Now, what does the Second Law say? It says that the entropy of the SYSTEM may only remain constant, or it may increase. The Second Law strictly forbids it to decrease!

Well, therefore let's think of the most favorable course of events - namely, that the entropy of the SYSTEM does not change, i.e., \(\Delta\) Ssystem \(=0\). It means that \(S_{\mathrm{C}}=\mathrm{SH}_{\mathrm{H}}\), or:

\[ \frac{Q_{\mathrm{C}}}{T_{\mathrm{C}}}=\frac{Q_{\mathrm{H}}}{T_{\mathrm{H}}} \]

The Equations \(9.1\) and \(9.3\) together constitute a system of two equations we can use to obtain the relation between \(W\) and \(Q \mathrm{H}\). From the latter one, we get that:

\[ Q_{\mathrm{C}}=Q_{\mathrm{H}} \frac{T_{\mathrm{C}}}{T_{\mathrm{H}}} \]

and by substituting this result to the Eq. 9.1, we obtain:

\[ W=Q_{\mathrm{H}}-Q_{\mathrm{H}} \frac{T_{\mathrm{C}}}{T_{\mathrm{H}}}=Q_{\mathrm{H}}\left(1-\frac{T_{\mathrm{C}} {T_{\mathrm{H}}}\right) \]

The ratio of the heat input to the work output we call the efficiency of the thermal engine and we use the symbol of \(\varepsilon\) for it:

\[ \epsilon_{\mathrm{E}}=\frac{W}{Q_{\mathrm{H}}}=1-\frac{T_{\mathrm{C}}}{T_{\mathrm{H}}}=\frac{T_{\mathrm{H}}-T_{\mathrm{C}} {T_{\mathrm{H}}} \]

where the subscript " \(E\) " indicates that \(\varepsilon\) is meant to be the efficiency of an engine. The result, often referred to as the Carnot Law 5, tells us that the lower is the difference between the hot source temperature \(T_{\mathrm{H}}\) and the heat sink temperature \(T_{\mathrm{C}}\), the lower is the engine's efficiency. The lower is the difference, the more the Second Law steals from us!

Now, let's consider what the Lord Kelvin's heat pump does. As shown in Fig. \(\PageIndex{1}\), the pump is nothing else than the heat engine we discussed above, but working in the opposite direction. In a single cycle, the pump "sucks in" a portion of input heat \(Q \mathrm{c}\) from the cold reservoir. A portion of input work \(W\) is also sent into the engine, where it is converted to heat, and added up to the heat input. The sum becomes the heat output \(Q \mathrm{H}\) :

\[ Q_{\mathrm{H}}=Q_{\mathrm{C}}+W \]

which is deposited into the hot reservoir. And again, how it is with the entropy. When the portion \(Q\) c is transferred from the cold reservoir to the pump, it's corresponds to the entropy transfer of \(Q \mathrm{C} / T \mathrm{C}\). And the transfer of heat from the pump to the hot reservoir corresponds to an entropy transfer of \(Q_{\mathrm{H}} / T_{\mathrm{H}}\). Now, using the same reasoning as before for the heat engine: in the case of an ideal heat pump, the entropy change of the combined system (cold reservoir) \(+(\) pump \()+(\) hot reservoir) is zero, so that:

\[ \frac{Q_{\mathrm{H}}}{T_{\mathrm{H}}}=\frac{Q_{\mathrm{C}}}{T_{\mathrm{C}}} \]

As before, the Eqs. \(9.5\) and \(9.6\) make a two-equation set, but we solve it now not for \(W\), but for \(Q\) H. The reader will easily find that:

\[ Q_{\mathrm{H}}=\frac{T_{\mathrm{H}}}{T_{\mathrm{H}}-T_{\mathrm{C}}} W \]

We define the efficiency \(\mathcal{E}_{\mathrm{P}}\) of the heat pump as the ratio of the output heat QH to the input work \(W\) :

\[ \epsilon_{\mathrm{P}}=\frac{Q_{\mathrm{H}}}{W}=\frac{T_{\mathrm{H}}}{T_{\mathrm{H}}-T_{\mathrm{C}}}=\frac{1}{\epsilon_{\mathrm{E}}} \]

So, the efficiency of a heat pump appears to be an inverse of the efficiency of a heat engine. What is the practical meaning of this result? The best answer we get by working an example. Suppose that the temperature of a "cold reservoir" available to a homeowner in Corvallis is \(12^{\circ} \mathrm{C}\) (in a moment, it will be shown that this is a reasonable value). The homeowner uses a heat pump and a conventional forced air central heating system that blows air of \(60^{\circ} \mathrm{C}\) temperature into her rooms. Let's first convert the temperatures to Kelvins: the temperature of the cold reservoir is \(T_{\mathrm{C}}=(273+12) \mathrm{K}=285\) \(\mathrm{K}\). The temperature of the hot reservoir is \((273+60) \mathrm{K}=333 \mathrm{~K}\). So, the efficiency of the homeowner's heat pump is:

\[ \epsilon_{\mathrm{P}}=\frac{333 K}{333 K-285 K}=6.94 \]

The homeowner’s pump needs a mechanical work input, right? In all avail- able heat pumps the mechanical work is delivered by electric motors. The efficiency of electric motors is very high. 90% is not unusual. So, by adjusting for the motor efficiency, the heat power the pump delivers to the house is 90% 6.94= 6.25 times the electric power used by the motor.

Before the homeowner installed the heat pump, she had used the old- fashion electric heating – the so-called “resistance electric heaters”. Their efficiency is 100%, meaning that 100% of the input electric power is converted by them to heat power. So, the conclusion is pretty straightforward: now, to get the same heat power as before, she needs 6.25 times less electric power than she needed before! A great deal, isn’t it?

Well, it would be so if her heat pump were ideal. But the efficiency of real heat pumps is lower. It may be even as low as 50% of the ideal E_P. So, it would be no 6.25, but only 3.12 times less. It still seems like a pretty good deal.

Professional heat pump installers do not use the symbol ε_P and term “efficiency”, instead they use the “Coefficient of Performance” (COF) which is essentially the same as the ε_P defined by us as Q_H/W .

The COF depends both on the temperature difference T_H T_C and on the construction of the heat pump mechanism (i.e., on how close it is to an “ideal heat engine”). In practice, the COP of the real machines varies from 3 to 7.

The homeowner in our example would do even better if she used not the forced air central heating system (the most common in the US), but underfloor heating system in which water of temperature 45^◦ is circulated through a “lattice” of tubes hidden under the floor surface. Then, according to the Eq. 9.7, the ideal COP value would be 9.6, and even if it’s lowered by 50% by the non-ideal design of the pump, it still would be an impressive 4.8.

By the way, it’s not a common knowledge that one can find a heat pump in almost every American kitchen. Because any refrigerator is nothing else than a heat pump. The cold reservoir is the refrigerator’s interior. And the hot reservoir is the ambient air. The heat pumps used for heating homes have a similar design as the machinery that is hidden inside your refrigerator. Only it’s much larger. More details of how a heat pump is built and how it

works can be found in several Web pages, for instance, in this one. There are several “clickable” items in this Web page, e.g., if you click on the Coefficient of Performance one, you’ll find much information about various factors that determine the COP value in practical heat pumps.

Shallow Geothermal Heating Implementation

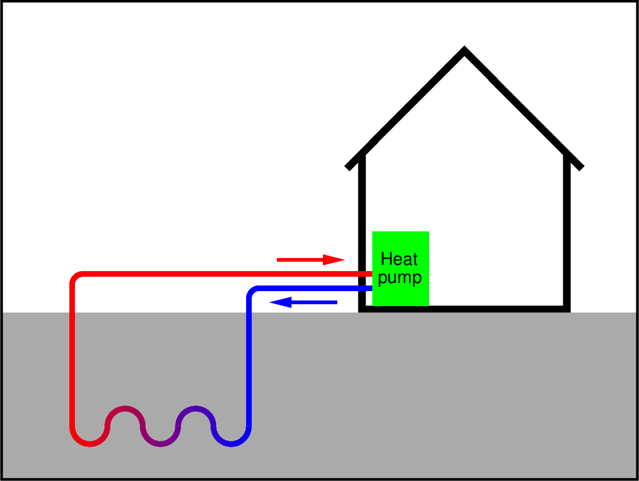
How can a heat pump be combined with geothermal energy? Well, this is simple. In always all areas inhabited by humans the subterranean tempera- ture at the depth of 10 ft and more is constant all over the year and is equal to the average annual air temperature in a given region. In the Willamette Valley, the annual average temperature of air is about 53^◦F, which corresponds to about 12^◦C (it’s why we used this temperature in the example above). In the US the subterranean temperature varies from 10 to 16 ^◦C. Therefore, by burying a long enough system of pipes with circulating water at the depth of 10 ft. or more, one can make an excellent “cold reservoir”.

An additional advantage of a heat pump is that it can work “in reverse”, so that in the summertime it can act as an air conditioner.

Other commonly used “cold reservoirs” are the air outside, or water in a creek or a pond, if they are nearby. Using outside air is the simplest and the most often used option. One can often see heat pumps in the backyards of people’s homes – they are equipped with huge fans that one can see and hear if the pump is on. But a disadvantage of such air cooling is that the lower is the temperature outside, the lower is the pump’s COP (one can clearly see in the Eq. 9.7 that if the temperature T_C decreases, then also the value of ε_P, or CPO, gets lower. Therefore, in areas where there are severe winters, homeowners have to install backup heaters they can turn on when the outside temperature falls so much that the heat pump practically stops working. And if the system is used as an air conditioner in summertime, a very hot outside air temperature lowers it efficiency.

Figure \(\PageIndex{1}\): : Shallow geothermal heating scheme. By reversing the action of the heat pump in summertime, the system changes into an air conditioner (source: aop).

Using water in a nonfreezing pond or in a nonfreezing creek as the cold reservoir has the advantage that the water temperature never falls below 0^◦C (32^◦F). So, there is no fear that the heat pump may stop working on a very cold winter day. But if the water in a pond or creek becomes warm in summertime, it may lower the efficiency of the system working in the air conditioning mode.

The advantage of the shallow geothermal system is that the temperature of the subterranean cold reservoir stays constant all the year round. So, the outside weather does not affect in any way the performance of the system, no matter if it’s in the heat pump mode, or in the air conditioning mode. The costs of installing a system of pipes ten or more feet underground (necessary), and a system of heating tubes under the floor (optional) may be discouraging. Yet, these are only one-time investments that will be paid back due to significantly lower heating bills.

_____________________________________________________________

1. An important reminder: the temperature in the expression for entropy, \(S=Q / T\), must always be taken as the absolute temperature, in Kelvins, and never in centi- grades \({ }^{\circ} \mathrm{C}\) or in Fahrenheits \({ }^{\circ} \mathrm{F}\).

2. Let's keep in mind that the Carnot Law is the efficiency of an ideal heat engine. In Chapter 3 it has been discussed how a real engine differs from an ideal one - namely, due to the irreversible processes associated with its functioning, it adds a portion of "extra entropy" \(S_{\text {EXTRA which }}\) has to be added to the right side of the Eq. 9.3. The calculations yield then an efficiency that is lower than \(\boldsymbol{E}_{\mathrm{E}}\) in the Eq. 9.4.