Recently several papers have been published on algorithms to calculate a length-\(2^M\) DFT more efficiently than a Cooley-Tukey FFT of any radix. They all have the same computational complexity and are optimal for lengths up through 16 and until recently was thought to give the best total add-multiply count possible for any power-of-two length. Yavne published an algorithm with the same computational complexity in 1968, but it went largely unnoticed. Johnson and Frigo have recently reported the first improvement in almost 40 years. The reduction in total operations is only a few percent, but it is a reduction.
The basic idea behind the split-radix FFT (SRFFT) as derived by Duhamel and Hollmann is the application of a radix-2 index map to the even-indexed terms and a radix-4 map to the odd- indexed terms. The basic definition of the DFT is:
\[C_k=\sum_{n=0}^{N-1}x_nW^{nk} \nonumber \]
with W=e-j2π/NW=e-j2π/N" role="presentation" style="position:relative;" tabindex="0">\(W=e^{-j2\pi /N}\) gives
\[C_{2k}=\sum_{n=0}^{N/2-1}\left [ x_n+x_{n+N/2} \right ]W^{2nk} \nonumber \]
for the even index terms, and
\[C_{4k+1}=\sum_{n=0}^{N/4-1}\left [ (x_n-x_{n+N/2})-j(x_{n+N/4}-x_{n+3N/4}) \right ]W^nW^{4nk} \nonumber \]
and
\[C_{4k+3}=\sum_{n=0}^{N/4-1}\left [ (x_n-x_{n+N/2})-j(x_{n+N/4}-x_{n+3N/4}) \right ]W^{3n}W^{4nk} \nonumber \]
for the odd index terms. This results in an L-shaped “butterfly" shown in Fig. 8.4.1 which relates a length-N DFT to one length-N/2 DFT and two length-N/4 DFT's with twiddle factors. Repeating this process for the half and quarter length DFT's until scalars result gives the SRFFT algorithm in much the same way the decimation-in-frequency radix-2 Cooley-Tukey FFT is derived. The resulting flow graph for the algorithm calculated in place looks like a radix-2 FFT except for the location of the twiddle factors. Indeed, it is the location of the twiddle factors that makes this algorithm use less arithmetic. The L- shaped SRFFT butterfly Fig. 8.4.1 advances the calculation of the top half by one of the \(M\) stages while the lower half, like a radix-4 butterfly, calculates two stages at once. This is illustrated for \(N=8\) in Fig. 8.4.2.

Fig. 8.4.1 SRFFT Butterfly
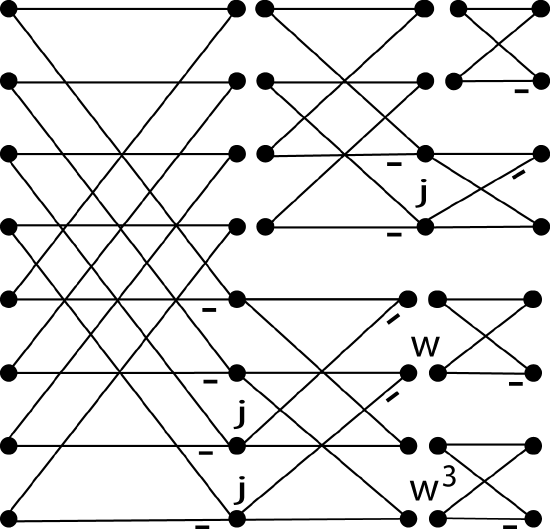
Fig. 8.4.2 Length-8 SRFFT
Unlike the fixed radix, mixed radix or variable radix Cooley-Tukey FFT or even the prime factor algorithm or Winograd Fourier transform algorithm , the Split-Radix FFT does not progress completely stage by stage, or, in terms of indices, does not complete each nested sum in order. This is perhaps better seen from the polynomial formulation of Martens. Because of this, the indexing is somewhat more complicated than the conventional Cooley-Tukey program.
A FORTRAN program is given below which implements the basic decimation-in-frequency split-radix FFT algorithm. The indexing scheme of this program gives a structure very similar to the Cooley-Tukey programs in and allows the same modifications and improvements such as decimation-in-time, multiple butterflies, table look-up of sine and cosine values, three real per complex multiply methods, and real data versions
FORTRAN Program implementing split-radix FFT algorithm
SUBROUTINE FFT(X,Y,N,M)
N2 = 2*N
DO 10 K = 1, M-1
N2 = N2/2
N4 = N2/4
E = 6.283185307179586/N2
A = 0
DO 20 J = 1, N4
A3 = 3*A
CC1 = COS(A)
SS1 = SIN(A)
CC3 = COS(A3)
SS3 = SIN(A3)
A = J*E
IS = J
ID = 2*N2
40 DO 30 I0 = IS, N-1, ID
I1 = I0 + N4
I2 = I1 + N4
I3 = I2 + N4
R1 = X(I0) - X(I2)
X(I0) = X(I0) + X(I2)
R2 = X(I1) - X(I3)
X(I1) = X(I1) + X(I3)
S1 = Y(I0) - Y(I2)
Y(I0) = Y(I0) + Y(I2)
S2 = Y(I1) - Y(I3)
Y(I1) = Y(I1) + Y(I3)
S3 = R1 - S2
R1 = R1 + S2
S2 = R2 - S1
R2 = R2 + S1
X(I2) = R1*CC1 - S2*SS1
Y(I2) =-S2*CC1 - R1*SS1
X(I3) = S3*CC3 + R2*SS3
Y(I3) = R2*CC3 - S3*SS3
30 CONTINUE
IS = 2*ID - N2 + J
ID = 4*ID
IF (IS.LT.N) GOTO 40
20 CONTINUE
10 CONTINUE
IS = 1
ID = 4
50 DO 60 I0 = IS, N, ID
I1 = I0 + 1
R1 = X(I0)
X(I0) = R1 + X(I1)
X(I1) = R1 - X(I1)
R1 = Y(I0)
Y(I0) = R1 + Y(I1)
60 Y(I1) = R1 - Y(I1)
IS = 2*ID - 1
ID = 4*ID
IF (IS.LT.N) GOTO 50
NOT_CONVERTED_YET: caption
Split-Radix FFT FORTRAN Subroutine
As was done for the other decimation-in-frequency algorithms, the input index map is used and the calculations are done in place resulting in the output being in bit-reversed order. It is the three statements following label 30 that do the special indexing required by the SRFFT. The last stage is length- 2 and, therefore, inappropriate for the standard L-shaped butterfly, so it is calculated separately in the DO 60 loop. This program is considered a one-butterfly version. A second butterfly can be added just before statement 40 to remove the unnecessary multiplications by unity. A third butterfly can be added to reduce the number of real multiplications from four to two for the complex multiplication when W has equal real and imaginary parts. It is also possible to reduce the arithmetic for the two- butterfly case and to reduce the data transfers by directly programming a length-4 and length-8 butterfly to replace the last three stages. This is called a two-butterfly-plus version. Operation counts for the one, two, two-plus and three butterfly SRFFT programs are given in the next section.
An improvement in operation count has been reported by Johnson and Frigo which involves a scaling of multiplying factors. The improvement is small but until this result, it was generally thought the Split-Radix FFT was optimal for total floating point operation count.




