6.2: Function of a Turnbuckle

Last updated
Save as PDF

Page ID: 95308

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

6.4.1 Function of a Turnbuckle

A turnbuckle is a metal coupling device consisting of an oblong piece, or barrel, internally threaded at both ends into which the corresponding sections of two threaded rods are screwed in order to form a unit that can be adjusted for tension or length. A right-hand thread is used at one end and a left-hand thread at the other end. The device either lengthens or shortens when the barrel is rotated. Each full turn of the barrel causes it to travel a distance p along each screw, where p is the pitch of the threads. Tightening the turnbuckle by one turn causes the rods to be drawn closer together by a distance 2p. That is, one turn to tighten causes the device to shorten by 2p. For n turns the shortening distance is 2np, where n need not be an integer. Turnbuckles are widely used in aircraft. Biplanes may use turnbuckles to adjust the tension on structural wires bracing their wings as discussed in example 6.10 below. Turnbuckles are also widely used with flexible cables in flight control systems.

Example 6.10 Rigging biplane landing and flying wires

An acrobatic biplane has a maximum gross weight of 1,700 lbs. and a wing span of 25 feet. The cross sections of the lower and upper wings are thin, so the wing structure is strengthened by external bracing. As shown in figure 6.21 the bracing consists of landing and flying wires connecting the fuselage to the wings at the interplane strut. Turnbuckles inserted in the landing and flying wires are used to pre-tension the wires by changing their length.

We will model the structural unit consisting of the lower wing, upper wing, interplane strut, landing wires, and flying wires as shown in figure 6.22(a). The left-hand wings are modeled as a pin-jointed truss. Bars 1-2 and 3-4 represent the spars in the lower wing and upper wing, respectively, and are of length L = 10 ft. The spars are made of Sitka spruce with a Young’s modulus parallel to the grain of 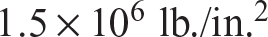$1.5 \times 1 0^{6}$ $math-1212.png$ lb./in.², and a cross-sectional area of 1.25 in.². Bar 1-3 represents the landing wire, bar 2-4 the flying wire, and the wires are made of stainless steel with a modulus of 30 × 10⁶ lb./in.² Each wire has a diameter of 0.125 in. Bar 1-4 is the interplane strut of length h equal to 4.3 ft., and it is assumed to be very stiff. The wings are specified to have a dihedral angle Γ = 4^°.

A representative biplane is shown with horizontal upper and lower wings. These wings are joined near their ends by vertical interplane struts. Diagonal wires also connect each wing to the other, with flying wires going from the upper wing to the lower wing, and landing wires doing the reverse, when looking from left to right. Cabane struts also connect the body of the aircraft to the upper wing. — Fig. 6.21 Aerobatics biplane.

Determine the number of turns in the flying wire turnbuckle n_F, and the number of turns in the landing wire turnbuckle n_L, such that the flying wire tension is 400 lb., and the dihedral is maintained at four degrees. The pitch of the turnbuckle threads is $p = 1 in . / (10 turns)$ $math-1213.png$ .

Solution. The structural model of the left-hand wing and bracing shown in figure 6.22(a) consists of five truss bars. The turnbuckle displacements are determined from the horizontal position of the wing. Free body diagrams of joints 1 and 4 are shown in figure 6.22(b). A vertical external force Q₂ is introduced at joint 1 so that its corresponding displacement q₂ can be determined in the application of Castigliano’s theorem. Displacement q₂ is specified from the wing’s required dihedral. That is $q_{2} = L sin Γ$ $math-1214.png$ , and after its determination external force Q₂ is set to zero.

From eq. (5.84) on page 136 the complementary energy for a homogenous truss bar subject to a uniform change in temperature is

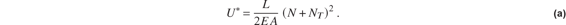
$\begin{align} U^{*} = \frac{L}{2 E A} {(N + N_{T})}^{2} . & (a) \end{align}$ $math-1215.png$

To account for the displacements of the turnbuckles in Castigliano’s second theorem we modify the axial temperature term in the complementary strain energy. The thermal axial force in the truss bar is obtained from eq. (3.75) on page 43:

$\begin{align} N_{T} = \int c β Δ T (s, z) t (s) d s = E A α Δ T . & (b) \end{align}$ $math-1216.png$

Let the thermal strain αΔT be replaced by the initial strain induced by the turnbuckle displacement Δ_T = 2np divided by the length of the bar containing the turnbuckle. That is, αΔT→Δ_T∕L. Then the complementary strain energy in eq. (a) that includes the displacement caused by the turnbuckle is

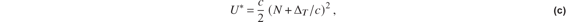
$\begin{align} U^{*} = \frac{c}{2} {(N + Δ_{T} / c)}^{2}, & (c) \end{align}$ $math-1217.png$

where the flexibility influence coefficient $c = L / (E A)$ $math-1218.png$ .

The upper and lower wing surfaces are of length cap L, while the vertical interplane strut between them is of height h. The strut connects nodes 1 and 4, with the numbering starting at the bottom-left node, and advancing counterclockwise around the structure. Nodes 2 and 3 are pinned, and restricted from displacement in any direction. The cross-wires connect the nodes diagonal to one another. Length along the wire between nodes 1 and 3, is denoted delta sub cap L, while length along the wire between nodes 4 and 2 is denoted delta sub cap F. External force cap Q sub 2 is applied vertically upward at node 1. Nodes 1 and 4 are isolated to show the forces on each. Node 4 has a downward force cap N sub 1 dash 4, a rightward horizontal force cap N sub 3 dash 4, and a diagonal force cap N sub 2 dash 4 at a clockwise angle theta from the horizontal. Node 1 has an upward force cap N sub 1 dash 4, a rightward horizontal force cap N sub 1 dash 2, and a diagonal force cap N sub 1 dash 3 at a counterclockwise angle theta from the horizontal. External force cap Q sub 2 is applied at node 1. — Fig. 6.22 (a) Structural model of the left-hand wing and bracing. (b) Free body diagrams.

The interplane strut subject to force N_1 − 4 is assumed to be rigid. Its flexibility influence coefficients vanishes and it does not contribute the elastic complementary strain energy. The complementary strain energy is

$\begin{align} U^{*} = 12 c_{W} {(N_{1 - 2})}^{2} + 12 c_{S T} {(N_{1 - 3} + Δ_{L} / c_{S T})}^{2} + 12 c_{S T} {(N_{2 - 4} + Δ_{F} / c_{S T})}^{2} + 12 c_{W} {(N_{3 - 4})}^{2} . & (d) \end{align}$ $math-1219.png$

The flexibility influence coefficients for the two wing spars is

$\begin{align} c_{W} = \frac{L}{E_{W} A_{W}} = \frac{120}{(1.5 \times 1 0^{6}) 1.25} = 64 \times 1 0^{-} 6 in . / lb, & (e) \end{align}$ $math-1220.png$

and the flexibility influence coefficients for the two wires is

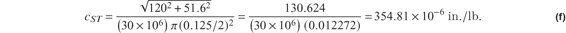
$\begin{align} c_{S T} = \frac{\sqrt{12 0^{2} + 51 . 6^{2}}}{(30 \times 1 0^{6}) π {(0.125 / 2)}^{2}} = \frac{130.624}{(30 \times 1 0^{6}) (0.012272)} = 354.81 \times 1 0^{- 6} in . / lb . & (f) \end{align}$ $math-1221.png$

Equilibrium equations at joint 1 in figure 6.22(b) are

$\begin{align} N_{1 - 3} cos θ + N_{1 - 2} = 0 Q_{2} + N_{1 - 4} + N_{1 - 3} sin θ = 0, & (g) \end{align}$ $math-1222.png$

and equilibrium equations at joint 4 are

$\begin{align} N_{3 - 4} + N_{2 - 4} cos θ = 0 N_{1 - 4} + N_{2 - 4} sin θ = 0 . & (h) \end{align}$ $math-1223.png$

The trigonometric functions of the angle θ are

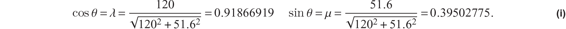
$\begin{align} cos θ = λ = \frac{120}{\sqrt{12 0^{2} + 51 . 6^{2}}} = 0.91866919 sin θ = μ = \frac{51.6}{\sqrt{12 0^{2} + 51 . 6^{2}}} = 0.39502775 . & (i) \end{align}$ $math-1224.png$

Now eliminate the bar force N_1 − 4 between the four equilibrium equations to get the three equations

$\begin{align} N_{1 - 3} λ + N_{1 - 2} = 0 N_{3 - 4} + N_{2 - 4} λ = 0 Q_{2} - N_{2 - 4} μ + N_{1 - 3} μ = 0 . & (j) \end{align}$ $math-1225.png$

The force N_2 − 4 in the flying wire is taken as the redundant. Solve the remaining bar forces from eq. (j) in terms of the redundant and force Q₂ to get

$\begin{align} N_{1 - 2} = - N_{2 - 4} λ + Q_{2} λ / μ N_{1 - 3} = N_{2 - 4} - Q_{2} / μ N_{3 - 4} = - N_{2 - 4} λ . & (k) \end{align}$ $math-1226.png$

Substitute the results for N_1 − 2, N_1 − 3, and N_3 − 4 from eq. (k) into the complementary strain energy (d) to find the energy in the form $U^{*} [N_{2 - 4}, Q_{2}]$ $math-1227.png$ with turnbuckle displacements Δ_L and Δ_F appearing in U_c as parameters.

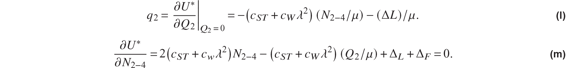
$\begin{matrix} q_{2} = {\frac{\partial U^{*}}{\partial Q_{2}}|}_{Q_{2} = 0} = - (c_{S T} + c_{W} λ^{2}) (N_{2 - 4} / μ) - (Δ L) / μ . & (l) \\ \frac{\partial U^{*}}{\partial N_{2 - 4}} = 2 (c_{S T} + c_{w} λ^{2}) N_{2 - 4} - (c_{S T} + c_{W} λ^{2}) (Q_{2} / μ) + Δ_{L} + Δ_{F} = 0 . & (m) \end{matrix}$ $math-1228.png$

Set $q_{2} = L sin Γ$ $math-1229.png$ in eq. (l) and solve for the landing wire turnbuckle displacement, followed by solving eq. (m) for the to find flying wire turnbuckle displacement. The results are

$\begin{align} Δ L = - (c_{S T} + c_{w} λ^{2}) N_{2 - 4} - μ L sin Γ and Δ F = - (c_{S T} + c_{w} λ^{2}) N_{2 - 4} + μ L sin Γ . & (n) \end{align}$ $math-1230.png$

Set $N_{2 - 4} = 400 lb.$ $math-1231.png$ to obtain the numerical results for the turnbuckle displacements and their number of turns as

$\begin{align} Δ L = - 3.41912 in. n_{L} = - 17.0956 turns Δ F = 3.19425 in. n_{F} = 15.9713 turns . & (o) \end{align}$ $math-1232.png$

The landing wire turnbuckle decreases the length between joints 1 and 3, and the flying wire turnbuckle increases the length between joints 2 and 4. The bar forces are

$\begin{align} N_{1 - 2} = N_{3 - 4} = - 367.468 lb . N_{1 - 3} = N_{2 - 4} = 400 lb . N_{1 - 4} = - 158.011 lb. . & (p) \end{align}$ $math-1233.png$

■

6.5 References

Bruhn, E. F., 1973, Analysis and Design of Flight Vehicle Structures, Jacobs Publishing, Inc., Carmel, Indiana, 46032, p. A8.42. (ISBN# 0-9615234-0-9)
Dowling, Norman E., 1993, Mechanical Behavior of Materials, Prentice Hall, Englewood Cliffs, New Jersey 07632, pp. 245–247.
Thornton, E. A., 1996, Thermal Structures for Aerospace Applications, AIAA Education Series, American Institute of Aeronautics and Astronautics, Inc., Reston, Virginia, pp. 118–121.
Warwick, Graham. “Big Fuel Savings Demand New Configurations,” November 7, 2011. Aviation Week.com.

6.6 Practice exercises

1. Each bar in the truss shown in figure 6.23 has a cross-sectional area of 1.0 in.², and a modulus of elasticity of 10⁷ psi. There is no change in temperature. Use Castigliano’s first theorem to find

a) the horizontal and vertical displacements of joint 1,

b) the stress in psi in each bar, and

c) the horizontal and vertical support reactions at joint 5.

2. The bars in the truss shown in figure 6.24 have the following cross-sectional areas: 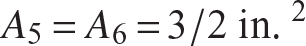$A_{1} = 1.0 {in.}^{2}$ $math-1234.png$ , $A_{2} = A_{4} = 2.0 {in.}^{2}$ $math-1235.png$ , $A_{3} = 1 / 2 {in.}^{2}$ $math-1236.png$ , $A_{5} = A_{6} = 3 / 2 {in.}^{2}$ $math-1237.png$ . The modulus of elasticity of each bar is 10⁷ psi. Compute the vertical displacement of the right-hand joint using Castigliano’s second theorem. Note this truss is statically determinate and all bar forces can be determined in terms of external load Q.

A truss structure is shown between a group of five nodes. Node 1 is is connected to nodes 2 through 5, but none of the other nodes are connected to one another. Using a standard x-y axis system, nodes 2 through 5 are all pinned to the same same wall 100 inches to the left of node 1. The element between nodes 1 and 2 is 90 degrees from the vertical. The element between nodes 1 and 3 is 60 degrees from the vertical. The element between nodes 1 and 4 is 45 degrees from the vertical. The element between nodes 1 and 5 is 30 degrees from the vertical. An external force is applied at node 1 at an angle of 45 degrees downward from the horizontal, and with a magnitude of 10000 pounds. — Fig. 6.23 Four bar truss of exercise 1.

The truss structure is composed of 6 elements and 5 nodes. Two nodes are pinned 40 inches apart on a vertical wall, while the next two are 30 inches away from the wall, with one node at the same height as each of the wall nodes. The final node is 30 inches away from the second lower node. Element 1 connects the two upper nodes. Element 2 connects the second upper node to the lower wall node. Element 3 connects the second upper and lower nodes. Element 4 connects the second upper node to the third lower node. Element 5 connects the first two lower nodes, while element 6 connects the second and third lower nodes. An external force, cap Q, is applied downward at the third lower node, with a magnitude of 30000 pounds. — Fig. 6.24 Six-bar truss for exercises 2 and 3.

3. Use Castigliano’s’ second theorem to compute the horizontal displacement of the right-hand joint of exercise 2.

4. The truss shown figure 6.25 consists of three bars: 1-4, 2-4, and 3-4. Each bar has the same cross-sectional area A, modulus of elasticity E, and the same coefficient of thermal expansion α. Bar 1-4 is subjected to a change in temperature ΔT from ambient temperature (the unstressed state), while bars 2-4 and 3-4 remain at ambient temperature. Use Castigliano’s first theorem to determine the horizontal displacement q₇ and the vertical displacement q₈ of joint 4.

A three bar truss connects a set of four nodes. Nodes 1, 2, and 3 are all 3 cap L below node 4, with node 2 being directly below node 4 in its unstressed state. Node 1 is 4 cap L to the left of node 2, while node 3 is 2.25 cap L to the right of node 2. Node 4’s displacement is denoted as q sub lower case delta vertically and q sub tau horizontally. Change in temperature delta cap T is applied only to element 1 dash 4. — Fig. 6.25 Three-bar truss of exercise 4.

5. The plane truss shown in figure 6.26 represents a single bay of a wing spar truss. For all bars: E = 75GPa and $α = 23.0 \times 1 0^{- 6} /^{°} C$ $math-1238.png$ . The cross-sectional areas of the bars are: 2580 mm² for the horizontal bars, 387 mm² for the vertical bars, and 2690 mm² for the diagonal bars. The upper horizontal bar is heated to 250^°C above the zero stress temperature, and all other bars remain at the zero stress temperature. Two 45 kN lift forces act at joints 1 and 2.

A truss connects a set of four nodes, with elements connecting each node to all of the other three, resulting in a shape resembling a rectangle with a cap X in the center. Node 1 is the bottom right node. Node 2 is the top right node. Node 3 is the bottom left node, which is pinned but free to displace vertically. Node 4 is the top left node, which is pinned and restricted from all displacement. The left-hand nodes are separated from the right-had nodes by a distance 1080 millimeters. The top and bottom nodes are separated by a distance 810 millimeters. An external heat source is applied to the element between between nodes 4 and 2, at a temperature of 250 degrees Celsius. An external force of 45 kilo Newtons is also applied upward at node 2. — Fig. 6.26 Six-bar truss in a single bay of a wing spar.

Use Castigliano’s first theorem to find

a) stiffness matrix in kN/mm,

b) displacement of all joints in mm,

c) all boundary reactions in kN, and

d) the stresses in MPa in each bar.

6. The truss shown in figure 6.27 consists of five bars: 1-2, 1-3, 1-4, 2-4, and 3-4. Each bar has the same cross-sectional area A and same modulus of elasticity E. The lengths of bars 1-2, 1-4, and 3-4 are the same, and are denoted by L. A horizontal force of magnitude P is applied to joint 1. Use Castigliano’s second theorem to determine the horizontal displacement q₅ of joint 3.

A square truss of side length cap L connects four corner nodes, numbered 1 through 4 beginning at the top-left corner, and advancing counterclockwise to node 4 in the top-right corner. Each node is connected to the nodes adjacent and diagonal to it, with the exception of nodes 2 and 3, which are not connected to each other. Node 2 is pinned and restricted from displacement in all directions. Node 3 is pinned, but still permitted to displace horizontally. — Fig. 6.27 Five-bar truss of exercise 6.

7. A simply supported, uniform beam of length L is subjected to a moment Q₁ at its left end as shown in figure 6.28. The material is homogeneous and linear elastic, the cross section is symmetric (I_xy = 0), and there are no thermal strains. The bending stiffness is EI. Use Castigliano’s second theorem to determine the rotation at (a) the left end, and (b) the right end. Neglect energy due to transverse shear deformation.

A simply supported beam is pinned at both ends, with the right end being free to displace horizontally. The beam lengthwise axis is denoted z and measured from zero at the left-edge to cap L at the right edge. The moment on the left edge is denoted cap Q sub 1, while the rotations at the left and right ends are denoted q sub 1 and q sub 2, respectively. — Fig. 6.28 Simply supported beam of exercise 7.

8. A coplanar frame is subjected to an end force Q₁ as shown in figure 6.29. The bars of the frame are uniform with axial stiffness EA and bending stiffness EI. Use Castigliano’s second theorem to find

a) the end rotation q₂, and

b) the vertical displacement q₃ at the joint.

A bent bar is fixed to the wall along its right edge. The outer bent portion is measured by local axis z sub 1, which is aligned with the bar’s central axis. The outer portion is cap L in length, and oriented such that its length forms the hypotenuse of a 3-4-5 right triangle, with the shallower angle being the angle with the horizontal. The inner bar is horizontal, and of length cap L along its local axis z sub 2, measured from the bend. An axial end force cap Q sub 1 is applied normal to the end of the bent portion of the bar. The end rotation of the bent portion of the bar is denoted q sub 2 clockwise. Vertical displacement of the joint between the straight and bent portions is denoted q sub 3 downward. — Fig. 6.29 Coplanar frame.

9. Consider the statically indeterminate, uniform beam shown in figure 6.30 that is subjected to a uniform, downward distributed load of intensity p. For small displacements assume that only the complementary strain energy in bending is significant. If the center support moves downward by the amount $0.01 p L^{4} / E I_{x x}$ $math-1239.png$ and remains attached to the beam, use Castigliano’s second theorem to find the reactions at the left and right supports.

A beam is placed under a uniformly distributed downward load p along its entire length cap L. The beam is pinned and restricted from all displacement at both ends and at the midpoint, cap L over 2. A z-y axis system is used, centered at the pinned left end, with z along the beam’s length and y upward normal to the beam. Displacements are denoted by w along the z axis and v along the y axis. — Fig. 6.30 Uniform beam of exercise 9.

10. The frame consists of three slender, uniform bars of length L, and two right angle bends. Assume the bends are rigid joints. Each member has a solid circular cross section of diameter d. A force P acts in the global X-direction at point A. Find the three displacement components $u_{A}, v_{A}, w_{A}$ $math-1240.png$ of point A in terms of P, L, d, and E using Castigliano’s second theorem. 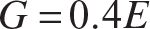Assume $G = 0.4 E$ $math-1241.png$ . Neglect deformations due to transverse shear.

A global cap X, cap Y, and cap Z axis system is used, with displacements denoted as u, v, and w along each respective axis. The frame is fixed at its base cap D. The first segment of length cap L is aligned along the cap X axis to point cap C. The second segment of length cap L is parallel to the cap Z axis to point cap B. The final segment of length cap L is parallel to the negative cap Y axis to point cap A. A force cap P is applied parallel to the cap X axis at point cap A. — Fig. 6.31 Space frame of exercise 10.

11. The rectangular space truss shown in the sketch consists of six bars: 1-2, 1-3, 1-4, 2-3, 2-4, and 3-4. The cross-sectional area of each bar is 200 mm². The temperature of bar 2-3 is increased by 30^°C above the stress free temperature, while the other five bars remain at the stress free temperature. Calculate the forces in all six bars. 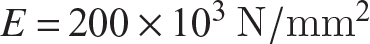The coefficient of thermal expansion $α = 7 \times 1 0^{- 6} /^{°} C$ $math-1242.png$ , and the modulus of elasticity $E = 200 \times 1 0^{3} N / {mm}^{2}$ $math-1243.png$ .

The truss is rectangular, with nodes advancing counterclockwise from 1 at the bottom left to 4 at the top left. The truss is 3000 millimeters in height, and 4000 mm in width. — Fig. 6.32 Space truss of exercise 11.

Note that m = 6, j = 4, and r = 0. Hence, 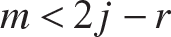$m < 2 j - r$ $math-1244.png$ , and this truss cannot support an external load without accelerating. However, under the self-straining caused by the temperature change, it is statically indeterminate internally.

12. Sketch the bending moment diagrams of bars 1-2 and 2-3 in the singly redundant frame shown in figure 6.33. Each bar has the same length L and flexural stiffness EI. Since the bars are slender, neglect deformations due to extension and transverse shear. Take the reaction moment at support point 1 as the redundant.

The frame forms the shape of an inverted cap L, with added support at the 90 degree turn in the middle. The vertical portion of length cap L extends from the fixed base at point 1 to the 90 degree turn at point 2. The horizontal portion of length cap L extends from the turn at point 2 to the right until reaching a support at point 3. — Fig. 6.33 Two-bar frame of exercise 12.

13. The aerodynamic advantages of high aspect-ratio (AR) wings are well known—long span reduces lift-induced drag and narrow chord promotes laminar flow to reduce skin-friction drag. However, a long wing span significantly increases the structural loads at the wing root requiring heaver components to safely transmit the loading to the fuselage. The truss-braced wing (TWB) is a method to reduce the load at the wing root. (It is the subject of research in AOE at Virginia Tech under a NASA program to achieve significant fuel savings for 737 type airplanes (Warwick, 2011)). A simplified model of TWB in this exercise is a single truss bar supporting a wing spar.

A wing spar is clamped at its root and supported by a truss bar that is pinned to the support at one end and pinned to the spar at the other end. Refer to figure 6.34. The spar is subjected to a span-wise distributed air load f_y(z) approximated by

$\begin{align} f_{y} (z) = \frac{3 L}{2 b} [1 - {(\frac{z}{b})}^{2}] 0 \leq (\frac{z}{b}) \leq 1 . & (a) \end{align}$ $math-1245.png$

where the lift on the wing is denoted by L and the wing span is denoted by b. The pin connection of the truss bar to the spar is at the span-wise distance s·b from the root, where the range of nondimensional parameter s is $0 < s \leq 1$ $math-1246.png$ .

The assemblage is statically indeterminate, and the statically determinate base structure is obtained by removing the lower pin support of the truss bar and replacing it by the redundant force Q which is also the tensile force in the truss bar. Refer to the right-hand sketch in figure 6.34. The condition of compatibility is the displacement corresponding to the redundant is equal to zero. Enforce compatibility by Castigliano’s second theorem given by

$\begin{align} q = \frac{\partial U^{*}}{\partial Q} = 0 U^{*} = \int_{0}^{s b} (\frac{M_{x}^{2}}{2 E I_{x x}} + \frac{N^{2}}{2 E A}) d z + \int_{s b}^{b} (\frac{M_{x}^{2}}{2 E I_{x x}}) d z + \frac{Q^{2} l_{s}}{2 E A_{s}} . & (b) \end{align}$ $math-1247.png$

where l_s is the length of the strut. Numerical data are listed in table 6.7.

A cantilever beam of length b is placed under an upward distributed load of f sub y of z. The global axis system is z along the beam’s length and y upward normal to beam. The beam has an additional support of a bar pinned to the supporting wall a distance h below the beam’s midplane and pinned to the beam’s midplane at a distance s times b from the wall, where s can vary from 0 to 1. The same beam, force, and supporting bar are used. However, the wall has been removed from the supporting bar’s left-hand pinned end and replaced with an axial tensile load cap Q. — Fig. 6.34 Truss-braced wing.

a) Plot the normalized bending moment at the wing root (M_x(0))∕M₀ versus s for $0.01 \leq s \leq 1$ $math-1248.png$ , where M₀ is the root bending moment of the cantilever wing; i.e., $M_{0} = - (3 / 8) b L$ $math-1249.png$

b) Plot the tensile normal stress $σ = Q / A_{s}$ $math-1250.png$ in the strut versus s for $0.01 \leq s \leq 1$ $math-1251.png$ .

c) If the allowable tensile stress in the strut is 30 ksi, what is the value of s to yield the smallest value of the ratio (M_x(0))∕M₀? What is the value of (M_x(0))∕M₀ for this particular s?

Table 6.7 Numerical data for the strut-braced wing

b, wing span	390 in.
h, vertical distance from the spar centroid to lower strut support	72 in.
A, cross-sectional area of the spar	23.88 in.²
I_xx, second area moment of the cross section of the spar	872.716 in.⁴
A_s, cross-sectional area of the strut (1.75 in. diameter)	2.40528 in.²
L, wing lift	50,000. lb.
E, modulus of elasticity for the spar and strut material	10 × 10⁶ 1b./in.²

Search

Text Color

Text Size

Margin Size

Font Type

6.4.1 Function of a Turnbuckle

6.5 References

6.6 Practice exercises