3.2: PV Diagram for Pure Systems
- Page ID
- 7483
In the previous discussion, we used the P-T diagram and were not concerned about changes in the volume of the system. If we want to follow changes in volume, we may construct P-v or T-v diagrams, in which we hold temperature (T) or pressure (P) constant. Let us consider the case of a P-v Diagram (Figure \(\PageIndex{4}\)).
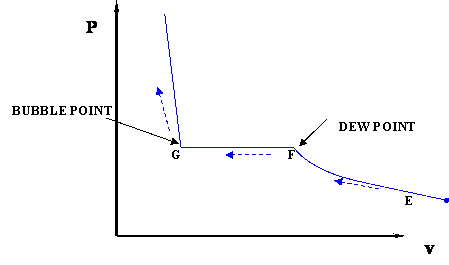
In this case temperature is being held constant; our substance is undergoing an isothermal compression process. Starting at E (all-vapor condition), an increase in pressure will result in a rather significant reduction in volume since the gas phase is compressible. If we keep compressing isothermally, we will end up at point F, where the gas will be saturated and the first droplet of liquid will appear. We have come to the two-phase condition, where liquid (L) and vapor (V) co-exist in equilibrium, for the first time, albeit an infinitesimal amount of liquid.
Once we reach the two-phase condition, what happens is not intuitive. While we keep on compressing by decreasing the volume (path F-G,) the pressure of the system remains constant; this condition continues until all the vapor has become liquid. Point G represents the last condition of liquid and vapor (L+V) coexistence, saturated liquid condition (liquid in equilibrium with an infinitesimal amount of vapor.) Once we have only liquid, if we keep on compressing (i.e., attempting to reduce liquid volume) we will observe a rapid increase in pressure, as indicated by the steep slope in the P-v diagram. This is because liquid is virtually incompressible, hence, a great deal of pressure is needed to cause a small reduction in volume.
It is important to recognize some points of this process. If we recall our previous definitions of basic concepts, we will recognize point F, where only a tiny quantity of liquid exists in an otherwise completely gaseous system (the dew point of the system at the given temperature). Similarly, Point G is the bubble point; only an infinitesimally small bubble of vapor exists in an otherwise liquid system.
But wait a second. Let us try to compare Figure 3.2.4 with Figure 3.1.2. Can we relate them to each other? Where is path F-G in Figure 3.2.4 represented in Figure 3.1.2 (repeated below)?
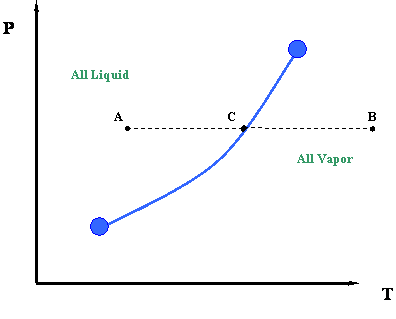
The answer is, path F-G is represented by one point in Figure 3.1.2; that is, point C. Recall, for a single-component system, dew points and bubble points are identical. During a phase transition, both pressure and temperature must remain constant for pure components.
Now, if we want to generate all the possible points that make up the vapor pressure curve in Figure 3.1.2, we would need to repeat the experiment for different temperatures. We would end up with a family of isotherms (each similar to the one presented in Figure 3.2.4). This is represented in Figure 3.2.5.
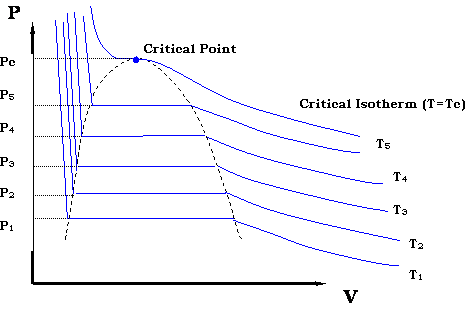
The zone where the isotherms become flat delineates the two-phase region. It is clearly seen that by plotting all the pairs in that zone (P1,T1), (P2,T2)… (Pc, Tc) we will be able to reproduce Figure 3.1.2.
If we now draw a line through all the Bubble Points in Figure 3.2.5, and then draw a line connecting all the Dew Points, we will end up with the Bubble Point Curve and the Dew Point Curve, respectively. It is clear that the two curves meet at the critical point (Pc, Tc). Furthermore, the two curves delineate the phase envelope, which contains the 2-phase region inside. If we “clean” Figure 3.2.5 a little, we end up with the phase envelope that is shown in Fig. 3.2.6.
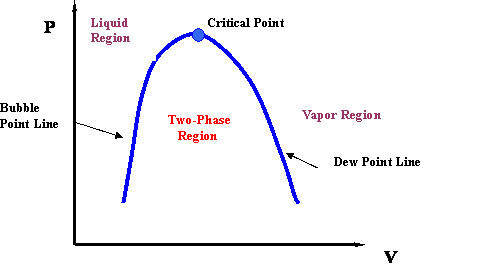
If you carefully follow the trend of the critical isotherm (@ T = Tc in Fig. 3.2.5), you will realize that it has a point of inflexion (change of curvature) at the critical point. Furthermore, the critical point also represents the maximum point (apex) of the P-v envelope. Mathematically, this information is conveyed by the expressions:
\[ \left( \frac{\partial P}{\partial V} \right)_{Pc,Tc} = \left( \frac{\partial^2 P}{\partial V^2} \right)_{Pc,Tc} = 0 \nonumber \]
which are usually known as the criticality conditions. These conditions are always satisfied at the critical point. We will comment more on this after we begin the discussion on Equations of State (EOS) — semi-empirical relationships that mathematically model the P-v-T behavior of fluids.


