1.2: Specifics of One-Time Pad
- Page ID
- 7314
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)People have been trying to send secret messages for roughly 2000 years, but there are really only 2 useful ideas from before 1900 that have any relevance to modern cryptography. The first idea is Kerckhoffs’ principle, which you have already seen. The other idea is one-time pad (OTP), which illustrates several important concepts, and can even still be found hiding deep inside many modern encryption schemes.
One-time pad is sometimes called "Vernam’s cipher" after Gilbert Vernam, a telegraph engineer who patented the scheme in 1919 . However, an earlier description of one-time pad was rather recently discovered in an 1882 text by Frank Miller on telegraph encryption.\(^{2}\)
In most of this book, secret keys will be strings of bits. We generally use the variable \(\lambda\) to refer to the length (# of bits) of the secret key in a scheme, so that keys are elements of the set \(\{0,1\}^{\lambda}\). In the case of one-time pad, the choice of \(\lambda\) doesn’t affect security \((\lambda=10\) is "just as secure" as \(\lambda=1000)\); however, the length of the keys and plaintexts must be compatible. In future chapters, increasing \(\lambda\) has the effect of making the scheme harder to break. For that reason, \(\lambda\) is often called the security parameter of the scheme.
In one-time pad, not only are the keys \(\lambda\)-bit strings, but plaintexts and ciphertexts are too. You should consider this to be just a simple coincidence, because we will soon encounter schemes in which keys, plaintexts, and ciphertexts are strings of different sizes.
The specific KeyGen, Enc, and Dec algorithms for one-time pad are given below:
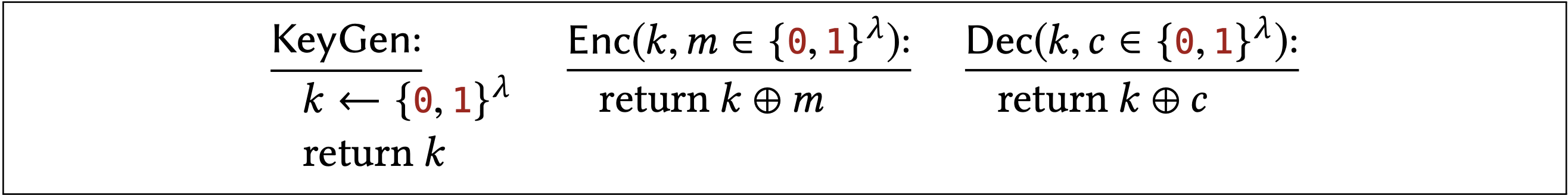
Recall that " \(k \leftarrow\{0,1\}^{\lambda "}\) means to sample \(k\) uniformly from the set of \(\lambda\)-bit strings. This uniform choice of key is the only randomness in all of the one-time pad algorithms. As we will see, all of its security stems from this choice of using the uniform distribution; keys that are chosen differently do not provide equivalent security.
Encrypting the following 20-bit plaintext \(m\) under the 20-bit key \(k\) using OTP results in the ciphertext c below:

Decrypting the following ciphertext c using the key \(k\) results in the plaintext \(m\) below:

Note that Enc and Dec are essentially the same algorithm (return the XOR of the two arguments). This results in some small level of convenience and symmetry when implementing one-time pad, but it is more of a coincidence than something truly fundamental about encryption (see Exercises \(1.12\) & \(2.5\)). Later on you’ll see encryption schemes whose encryption & decryption algorithms look very different.
Correctness
The first property of one-time pad that we should confirm is that the receiver does indeed recover the intended plaintext when decrypting the ciphertext. Without this property, the thought of using one-time pad for communication seems silly. Written mathematically:
For all \(k, m \in\{0,1\}^{\lambda}\), it is true that \(\operatorname{Dec}(k, \operatorname{Enc}(k, m))=m\).
Proof
This follows by substituting the definitions of OTP Enc and Dec, then applying the properties of xOR listed in Chapter \(0.3\). For all \(k, m \in\{0,1\}^{\lambda}\), we have:
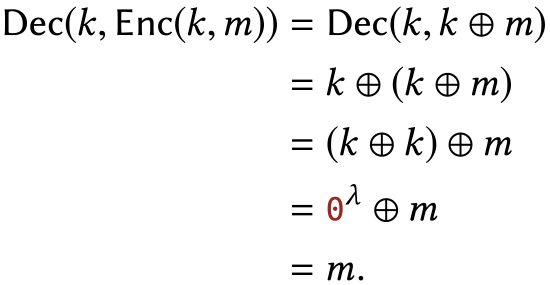
Encrypting the following plaintext \(m\) under the key \(k\) results in ciphertext \(c\), as follows:

Decrypting \(c\) using the same key \(k\) results in the original \(m\) :

Security
Suppose Alice and Bob are using one-time pad but are concerned that an attacker sees their ciphertext. They can’t presume what an attacker will do after seeing the ciphertext. But they would like to say something like, "because of the specific way the ciphertext was generated, it doesn’t reveal any information about the plaintext to the attacker, no matter what the attacker does with the ciphertext."
We must first precisely specify how the ciphertext is generated. The Enc algorithm already describes the process, but it is written from the point of view of Alice and Bob. When talking about security, we have to think about what Alice and Bob do, but from the eavesdropper’s point of view! From Eve’s point of view, Alice uses a key that was chosen in a specific way (uniformly at random), she encrypts a plaintext with that key using OTP, and finally reveals only the resulting ciphertext (and not the key) to Eve.
More formally, from Eve’s perspective, seeing a ciphertext corresponds to receiving an output from the following algorithm:

It’s crucial that you appreciate what this \(\texttt{EAVESDROP}\) algorithm represents. It is meant to describe not what the attacker does, but rather the process (carried out by Alice and Bob!) that produces what the attacker sees. We always treat the attacker as some (unspecified) process that receives output from this \(\texttt{EAVESDROP}\) algorithm. Our goal is to say something like "the output of \(\texttt{EAVESDROP}\) doesn’t reveal the input \(m\) ".
\(\texttt{EAVESDROP}\) is a randomized algorithm - remember that " \(k \leftarrow\{0,1\}^{\lambda "}\) means to sample \(k\) from the uniform distribution on \(\lambda\)-bit strings. If you call \(\texttt{EAVESDROP}\) several times, even on the same input, you are likely to get different outputs. Instead of thinking of "\(\texttt{EAVESDROP}\) \((m)\) " as a single string, you should think of it as a probability distribution over strings. Each time you call \(\texttt{EAVESDROP}\) \((m)\), you see a sample from that distribution.
Let’s take \(\lambda=3\) and work out by hand the distributions \(\texttt{EAVESDROP}\) (010) and \(\texttt{EAVESDROP}\) (111). In each case \(\texttt{EAVESDROP}\) chooses a value of \(k\) uniformly in \(\{0,1\}^{3}\) - each of the possible values with probability \(1 / 8\). For each possible choice of \(k\), we can compute what the output of \(\texttt{EAVESDROP}\) (c) will be:
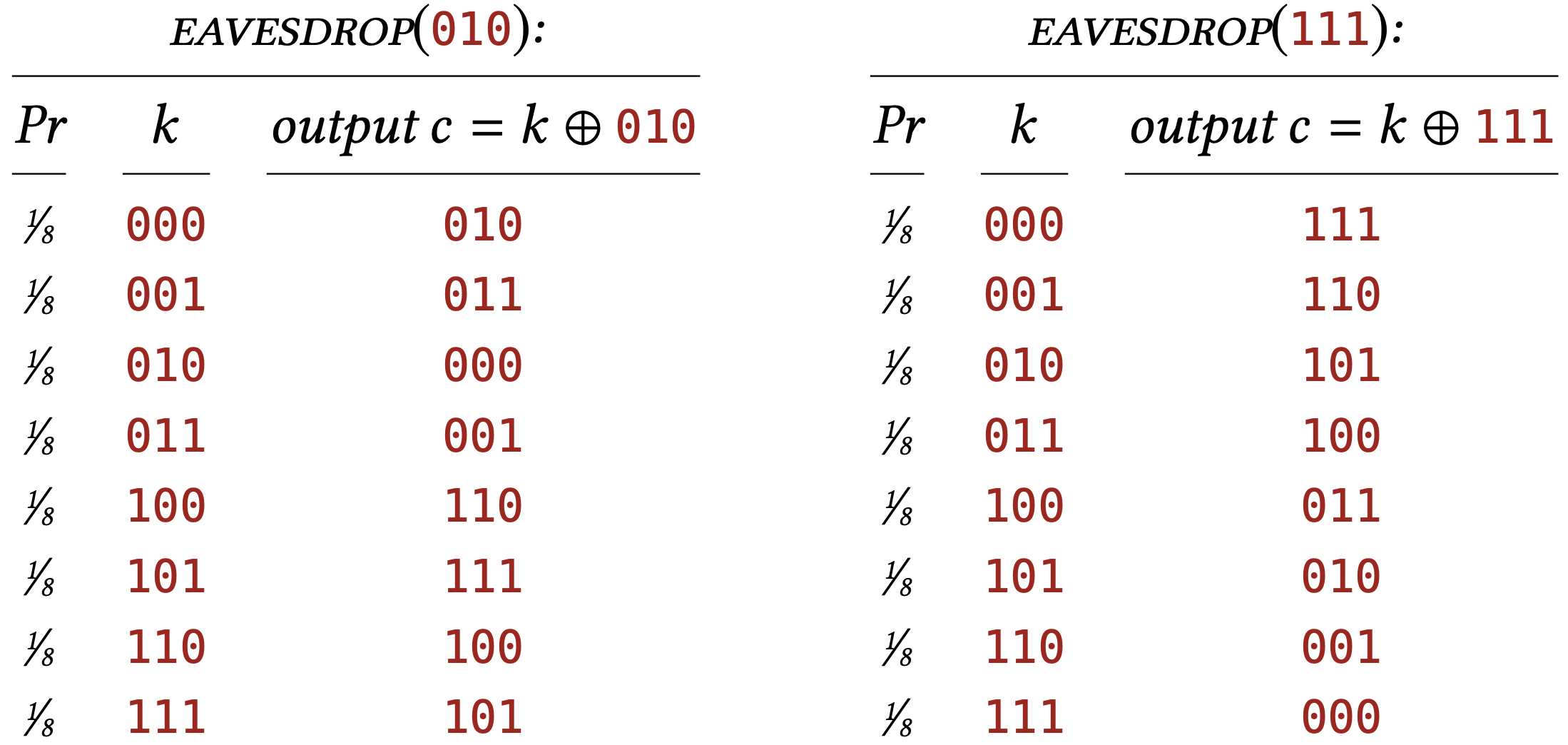
So the distribution \(\texttt{EAVESDROP}\) \((010)\) assigns probabilty \(1 / 8\) to 010 , probability \(1 / 8\) to 011 , and so on.
In this example, notice how every string in \(\{0,1\}^{3}\) appears exactly once in the \(c\) column of \(\texttt{EAVESDROP}\) \((010)\). This means that \(\texttt{EAVESDROP}\) assigns probability \(1 / 8\) to every string in \(\{0,1\}^{3}\), which is just another way of saying that the distribution is the uniform distribution on \(\{0,1\}^{3}\). The same can be said about the distribution \(\texttt{EAVESDROP}\)(111), too. Both distributions are just the uniform distribution in disguise!
There is nothing special about 010 or 111 in these examples. For any \(\lambda\) and any \(m \in\) \(\{0,1\}^{\lambda}\), the distribution \(\texttt{EAVESDROP}\) \((m)\) is the uniform distribution over \(\{\theta, 1\}^{\lambda}\).
Claim 1.3 For every \(m \in\{0,1\}^{\lambda}\), the distribution \(\texttt{EAVESDROP}\) \((m)\) is the uniform distribution on \(\{0,1\}^{\lambda}\). Hence, for all \(m, m^{\prime} \in\{0,1\}^{\lambda}\), the distributions \(\texttt{EAVESDROP}\) \((m)\) and \(\texttt{EAVESDROP}\) \(\left(m^{\prime}\right)\) are identical.
Proof
Arbitrarily fix \(m, c \in\{0,1\}^{\lambda}\). We will calculate the probability that \(\texttt{EAVESDROP}\) \((m)\) produces output \(c\). That event happens only when \[c=k \oplus m \Longleftrightarrow k=m \oplus c .\] The equivalence follows from the properties of xOR given in Section 0.3. That is, \[\operatorname{Pr}[\text { \(\texttt{EAVESDROP}\) }(m)=c]=\operatorname{Pr}[k=m \oplus c],\] where the probability is over uniform choice of \(k \leftarrow\{0,1\}^{\lambda}\).
We are considering a specific choice for \(m\) and \(c\), so there is only one value of \(k\) that makes \(k=m \oplus c\) true (causes \(m\) to encrypt to \(c\) ), and that value is exactly \(m \oplus c\). Since \(k\) is chosen uniformly from \(\{0,1\}^{\lambda}\), the probability of choosing the particular value \(k=m \oplus c\) is \(1 / 2^{\lambda}\)
In summary, for every \(m\) and \(c\), the probability that \(\texttt{EAVESDROP}\) \((m)\) outputs \(c\) is exactly \(1 / 2^{\lambda}\). This means that the output of \(\texttt{EAVESDROP}\) \((m)\), for any \(m\), follows the uniform distribution.
One way to interpret this statement of security in more down-to-earth terms:
If an attacker sees a single ciphertext, encrypted with one-time pad, where the key is chosen uniformly and kept secret from the attacker, then the ciphertext appears uniformly distributed.
Why is this significant? Taking the eavesdropper’s point of view, suppose someone chooses a plaintext \(m\) and you get to see the resulting ciphertext - a sample from the distribution \(\texttt{EAVESDROP}\) \((m)\). But this is a distribution that you can sample from yourself, even if you don’t know \(m\) ! You could have chosen a totally different \(m^{\prime}\) and run \(\texttt{EAVESDROP}\)( \(\left.m^{\prime}\right)\) in your imagination, and this would have produced the same distribution as \(\texttt{EAVESDROP}\) \((m)\). The "real" ciphertext that you see doesn’t carry any information about \(m\) if it is possible to sample from the same distribution without even knowing \(m\) !
Discussion
- Isn’t there a paradox? Claim \(1.2\) says that \(c\) can always be decrypted to get \(m\), but Claim \(1.3\) says that \(c\) contains no information about \(m\) ! The answer to this riddle is that Claim \(1.2\) talks about what can be done with knowledge of the key \(k\) (Alice & Bob’s perspective). Claim \(1.3\) talks about the output distribution of the \(\texttt{EAVESDROP}\) algorithm, which doesn’t include \(k\) (Eve’s perspective). In short, if you know \(k\), then you can decrypt \(c\) to obtain \(m\); if you don’t know \(k\), then \(c\) carries no information about \(m\) (in fact, it looks uniformly distributed). This is because \(m, c, k\) are all correlated in a delicate way. \({ }^{3}\)
- Isn’t there another paradox? Claim \(1.3\) says that the output of \(\texttt{EAVESDROP}\) \((m)\) doesn’t depend on \(m\), but we can see the \(\texttt{EAVESDROP}\) algorithm literally using its argument \(m\) right there in the last line! The answer to this riddle is perhaps best illustrated by the previous illustrations of the \(\texttt{EAVESDROP}\) \((010)\) and \(\texttt{EAVESDROP}\)(111) distributions. The two tables of values are indeed different (so the choice of \(m \in\) \(\{010,111\}\) clearly has some effect), but they represent the same probability distribution (since order doesn’t matter). Claim \(1.3\) considers only the resulting probability distribution.
- You probably think about security in terms of a concrete "goal" for the attacker: recover the key, recover the plaintext, etc. Claim \(1.3\) doesn’t really refer to attackers in that way, and it certainly doesn’t specify a goal. Rather, we are thinking about security by comparing to some hypothetical "ideal" world. I would be satisfied if the attacker sees only a source of uniform bits, because in this hypothetical world there are no keys and no plaintexts to recover! Claim \(1.3\) says that when we actually use OTP, it looks just like this hypothetical world, from the attacker’s point of view. If we imagine any "goal" at all for the attacker in this kind of reasoning, it’s to detect that ciphertexts don’t follow a uniform distribution. By showing that the attacker can’t even achieve this modest goal, it shows that the attacker couldn’t possibly achieve other, more natural, goals like key recovery and plaintext recovery.
Limitations
One-time pad is incredibly limited in practice. Most notably:
- Its keys are as long as the plaintexts they encrypt. This is basically unavoidable (see Exercise 2.11) and leads to a kind of chicken-and-egg dilemma in practice: If two users want to privately convey a \(\lambda\)-bit message, they first need to privately agree on a \(\lambda\)-bit string.
- A key can be used to encrypt only one plaintext (hence, "one-time" pad); see Exercise 1.6. Indeed, we can see that the \(\texttt{EAVESDROP}\) subroutine in Claim \(1.3\) provides no way for a caller to guarantee that two plaintexts are encrypted with the same key, so it is not clear how to use Claim \(1.3\) to argue about what happens in one-time pad when keys are intentionally reused in this way.
\({ }^{2}\) See the article Steven M. Bellovin: "Frank Miller: Inventor of the One-Time Pad." Cryptologia 35 (3), \(2011 .\)
\({ }^{3}\) This correlation is explored further in Chapter \(3 .\) Despite these limitations, one-time pad illustrates fundamental ideas that appear in most forms of encryption in this course.


