2.1.2 Ohms Law and Classical Physics
- Page ID
- 2755
In this subchapter we will look at the classical treatment of the movement of electrons inside a material in an electrical field.
- In the preceding subchapter we obtained the most basic formulation of Ohms law, linking the specific conductivity to two fundamental material parameters:
\[\sigma=q\cdot n\cdot \mu\]
For a homogeneous and isotropic material (e.g. polycrystalline metals or single crystal of cubic semiconductors), the concentration of carriers n and their mobility µ have the same value everywhere in the material, and the specific conductivity σ is a scalar.
- This is boring, however. So let's look at useful complications:
In general terms, we may have more than one kind of carrier (this is the common situation in semiconductors) and n and µ could be functions of the temperature T, the local field strengthEloc resulting from an applied external voltage, the detailed structure of the material (e.g. the defects in the lattice), and so on.
- We will see that these complications are the essence of advanced electronic materials (especially semiconductors), but in order to make life easy we first will restrict ourselves to the special class of ohmic materials.
- We have seen before that this requires n and µ to be independent of the local field strength. However, we still may have a temperature dependence of σ; even commercial ohmic resistors, after all, do show a more or less pronounced temperature dependence - their resistance increases roughly linearly with T.
In short, we are treating metals, characterized by a constant density of one kind of carriers (=electrons) in the order of 1 ...3 electrons per atom in the metal.
Basic Equations and the Nature of the "Frictional Force"
We consider the electrons in the metal to be "free", i.e. they can move freely in any direction - the atoms of the lattice thus by definition do not impede their movement
- The (local) electrical field E then exerts a force F = – e · Eloc on any given electron and thus accelerates the electrons in the field direction (more precisely, opposite to the field direction because the field vector points from + to – whereas the electron moves from – to +).
- In the fly swarm analogy, the electrical field would correspond to a steady airflow - some wind - that moves the swarm about with constant drift velocity.
Now, if a single electron with the (constant) mass m and momentum p is subjected to a force F, the equation of motion from basic mechanics is
\[\underline{F}=\dfrac{\text{d}\underline{p}}{\text{d}t}=\dfrac{m\cdot \text{d}\underline{v}}{\text{d}t}\]
- Note that p does not have to be zero when the field is switched on.
If this would be all, the velocity of a given electron would acquire an ever increasing component in field direction and eventually approach infinity. This is obviously not possible, so we have to bring in a mechanism that destroys an unlimited increase in v.
- In classical mechanics this is done by introducing a frictional force Ffr that is proportional to the velocity.
\[\underline{F}_{\text{fr}}=-k_{fr}\cdot\underline{v}\]
- with kfr being some friction constant. But this, while mathematically sufficient, is devoid of any physical meaning with regard to the moving electrons.
- There is no "friction" on an atomic scale! Think about it! Where should a friction force come from? An electron feels only forces from two kinds of fields - electromagnetic and gravitational (neglecting strange stuff from particle physics). So we have to look for another approach.
What friction does to big classical bodies is to dissipate ordered kinetic energy of the moving body to the environment. Any ordered movement gets slowed down to zero (surplus) speed, and the environment gets somewhat hotter instead, i.e. unordered movement has increased.
- This is called energy dissipation, and that is what we need: Mechanisms that take kinetic energy away from an electron and "give" it to the crystal at large. The science behind that is called (Statistical) Thermodynamics - we have encounterd it before.
The best way to think about this, is to assume that the electron, flying along with increasing velocity, will hit something else along its way every now and then; it has a collision with something else, it will be scattered at something else.
- This collision or scattering event will change its momentum, i.e. the magnitude and the direction of v, and thus also its kinetic energy Ekin, which is always given by
\[E_{\text{kin}}=\dfrac{m\cdot\underline{\text{v}}^2}{2}=\dfrac{\underline{p}\cdot \text{v}}{2}\]
In other words, we consider collisions with something else, i.e. other particles (including "pseudo" particles), where the total energy and momentum of all the particles is preserved, but the individual particle looses its "memory" with respect to its velocity before the collision, and starts with a new momentum after every collision.
What are the "partners" for collisions of an electron, or put in standard language, what are the scattering mechanisms? There are several possibilities:
- Other electrons. While this happens, it is not the important process in most cases. It also does not decrease the energy contained in the electron movement - the losses of some electron are the gains of others.
- Defects, e.g. foreign atoms, point defects or dislocations. This is a more important scattering mechanism and moreover a mechanism where the electron can transfer its surplus energy (obtained through acceleration in the electrical field) to the lattice, which means that the material heats up
- Phonons, i.e. "quantized" lattice vibrations traveling through the crystal. This is the most important scattering mechanism.
Now that is a bit strange. While we (hopefully) have no problem imagining a crystal lattice with all atoms vibrating merrily, there is no immediate reason to consider these vibrations as being localized (whatever this means) and particle-like.
- You are right - but nevertheless: The lattice vibrations indeed are best described by a bunch of particle-like phonons careening through the crystal.
- This follows from a quantum mechanical treatment of lattice vibrations. Then it can be shown that these vibrations, which contain the thermal energy of the crystal, are quantized and show typical properties of (quantum) particles: They have a momentum, and an energy given by hν (h = Plancks constant, ν = frequency of the vibration).
Phonons are a first example of "pseudo" particles; but there is no more "pseudo" to phonons than there is to photons.
- We will not go into more details here. All we need to know is that a hot crystal has more phonons and more energetic phonons than a cold crystal, and treating the interaction of an electron with the lattice vibration as a collision with a phonon gives not only correct results, it is the only way to get results at all.
At this point comes a crucial insight: It would be far from the truth to assume that only accelerated electrons scatter; scattering happens all the time to all the electrons moving randomly about because they all have some thermal energy. Generally, scattering is the mechanism to achieve thermal equilibrium and equidistribution of the energy of the crystal.
- If electrons are accelerated in an electrical field and thus gain energy in excess of thermal equilibrium, scattering is the way to transfer this surplus energy to the lattice which then will heat up. If the crystal is heated up from the outside, scattering is the mechanism to turn heat energy contained in lattice vibrations to kinetic energy of the electrons.
- Again: Even without an electrical field, scattering is the mechanism to transfer thermal energy from the lattice to the electrons (and back). Generally, scattering is the mechanism to achieve thermal equilibrium and equidistribution of the energy of the crystal.
- Our free electrons in metals behave very much like a gas in a closed container. They careen around with some average velocity that depends on the energy contained in the electron gas, which is - in classical terms- a direct function of the temperature.
Averaging over Random Scattering Events
Lets look at some figures illustrating the scattering processes.
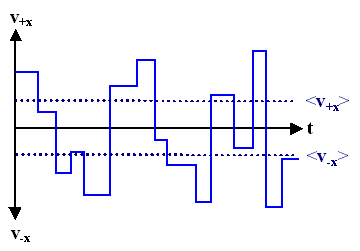
- Shown here is the magnitude of the velocity v ±x of an electron in +x and –x direction without an external field. The electron moves with constant velocity until it is scattered, then it continues with some new velocity.
- The scattering processes, though unpredictable at single events, must lead to the averages of the velocity, which is characteristic for the material and its conditions.
- The plural in "averages" is intentional: there are different averages of the velocity
- Whereas <v> = 0, <v> has a finite value; this is also true for <vx> = – <v–x> . Consult the"fly swarm modul" if you are unsure about this.
- From classical thermodynamics we know that the (classical) electron gas in thermal equilibrium with the environment contains the energy Ekin = (1/2)kT per particle and degree of freedom, with k = Boltzmanns constant and T = absolute temperature. The three degrees of freedom are the velocities in x-, y- and z-direction, so we must have
\[E_{\text{kin,x}}=\frac12 \cdot m \cdot <\text{v}_\text{x}>^2=\frac12 \cdot \text{k}T\\<\text{v}_\text{x}>=\left(\frac{\text{k}T}{m}\right)^{1/2}\]
- For the other directions we have exactly the same relations, of course. For the total energy we obtain
\[E_{kin}=\frac{m\,\cdot <\text{v}_\text{x}^2>}{2}+\frac{m\,\cdot <\text{v}_\text{y}^2>}{2}+\frac{m\,\cdot <\text{v}_\text{z}^2>}{2}=\frac{m\,\cdot <\text{v}^2>}{2}=\frac{m\,\cdot <\text{v}_\text{0}^2>}{2}=\frac{3\text{k}T}{2}\]
- with v0 = <v>. v0 is thus the average velocity of a carrier careening around in a crystal.
- At this point you should stop a moment and think about just how fast those electrons will be careening around at room temperature (300K) without plugging numbers in the equation. Got a feeling for it? Probably not. So look at the exercise question (and the solution) further down!.
- Now you should stop another moment and become very aware of the fact that this equation is from purely classical physics. It is absolutely true for classical particles - which electrons are actually not. Electrons obey the Pauli principle, i.e. they behave about as non-classical behavior as it is possible. This should make you feel a bit uncomfortable. Maybe the equation from above is not correct for electrons then? Indeed - it isn't. Why, we will see later; also how we can "repair" the situation!
Now lets turn on an electrical field. It will accelerate the electrons between the collisions. Their velocity in field direction then increases linearly from whatever value it had right after a collision to some larger value right before the next collision.
- In our diagram from above this looks like this:

- Here we have an electrical field that accelerates electrons in in x-direction (and "brakes" in –x direction). Between collisions, the electron gains velocity in +x-direction at a constant rate (= identical slope).
- The average velocity in +xdirections, <v+x>, is now larger than in –x direction, <v–x>.
- However, beware of the pitfalls of schematic drawings: For real electrons the difference is very small as we shall see shortly; the slope in the drawing is very exaggerated.
- The drift velocity is contained in the difference <v+x> – <v–x>; it is completely described by the velocity gain between collisions. For obtaining a value, we may neglect the instantaneous velocity right after a scattering event because they average to zero anyway and just plot the velocity gain in a simplified picture; always starting from zero after a collision.

- The picture now looks quite simple; but remember that it contains some not so simple averaging.
- At this point it is time to define a very meaningfulnew average quantity:
- The mean time between collisions, or more conventional, the mean time τ for reaching the drift velocity v in the simplified diagram. We also call τ the mean scattering time or just scattering time for short.
This is most easily illustrated by simplifying the scattering diagram once more: We simply use just onetime - the average - for the time that elapses between scattering events and obtain:
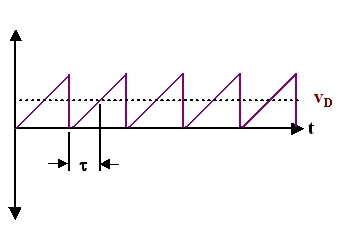
- This is the standard diagram illustrating the scattering of electrons in a crystal usually found in text books; the definition of the scattering time τ is included
- It is highly idealized, if not to say just wrong if you compare it to the correct picture above. Of course, the average velocity of both pictures will give the same value, but that's like saying that the average speed vaof all real cars driving around in a city is the same as the average speed of ideal model cars all going at va all the time.
- Note that τ is only half of the average time between collisions.
So, while this diagram is not wrong, it is a highly abstract rendering of the underlying processes obtained after several averaging procedures. From this diagram only, no conclusion whatsoever can be drawn as to the average velocities of the electrons without the electrical field!
New Material Parameters and Classical Conductivity
With the scattering concept, we now have two new (closely related) material parameters:
- The mean (scattering) time τ between two collisions as defined before, and a directly related quantity:
- The mean free path l between collisions; i.e. the distance travelled by an electron (on average) before it collides with something else and changes its momentum. We have
\[l=2\tau\,\cdot\,(\text{v}_0+\text{v}_\text{D})\]
- Note that v0 enters the defining equation for l, and that we have to take twice the scattering time τbecause it only refers to half the time between collisions!
After we have come to this point, we now can go on: Using τ as a new parameter, we can rewrite Newtons equation from above:
\[\dfrac{d\underline{\text{v}}}{dt}=\frac{\Delta\text{v}}{\Delta\text{t}}=\frac{\text{v}_D}{\tau}\]
- It is possible to equate the differential quotient with the difference quotient, because the velocity change is constant. From this we obtain
\[\begin{align}\frac{\text{v}_D}{\tau}&=-\frac{E\,\cdot\,\text{e}}{m}\\\Rightarrow\;\text{v}_D&=-\frac{E\,\cdot\,\text{e}\,\cdot\,\tau}{m}\end{align}\]
Inserting this equation for vD in the old definition of the current density j = – n · e · vD and invoking the general version of Ohms law, j = σ · E, yields
\[j=\frac{n\,\cdot\,\text{e}^2\,\cdot\,\tau}{m}\cdot\,E=\sigma\,\cdot\,E\]
- This gives us the final result
\[\frac{n\,\cdot\,\text{e}^2\,\cdot\,\tau}{m}=\sigma\]
This is the classical formula for the conductivity of a classical "electron gas" material; i.e. metals. The conductivity contains the density n of the free electrons and their mean scattering time τ as material parameters.
- We have a good idea about n, but we do not yet know τclass, the mean classical scattering time for classical electrons. However, since we know the order of magnitude for the conductivity of metals, we may turn the equation around and use it to calculate the order of magnitude of τclass. If you do the exercise farther down, you will see that the result is:
\[\tau_\text{class}=\frac{\sigma\,\cdot\,m}{n\,\cdot\,\text{e}^2}=\left(10^{-13}\,\ldots\,10^{-15}\right)\,\text{sec}\]
- "Obviously" (as stated in many text books), this is a value that is far too small and thus the classical approach must be wrong. But is it really too small? How can you tell without knowing a lot more about electrons in metals?
- Let's face it: you can't !!. So let's look at the mean free path l instead. We have
\[l=2\,\cdot\,\tau\,\cdot\,(\text{v}_0+\text{v}_D)\\\text{and}\\(\text{v}_0)^2=\frac{3\text{k}T}{m}\]
- The last equation gives us a value v0 ≈ 104 m/s at room temperature! Now we need vD, and this we can estimate from the equation given above to vD = – E · τ · e/m ≈ 1 mm/sec, if we use the value for τ dictated by the measured conductivities. It is much smaller than v0 and can be safely neglected in calculating l.
We thus can rewrite the equation for the conductivity and obtain
\[\sigma=\frac{n\,\cdot\,\text{e}^2\,\cdot\,l}{2\,\cdot\,m\,\cdot\,(\text{v}_0+\text{v}_D)}\]
Knowing σ from experiments, but not l, allows to determine l. The smallest possible mean free path lminbetween collisions (for vD = 0) thus is
\[l_\text{min}=\frac{2\,\cdot\,m\,\cdot\,\text{v}_0\,\cdot\,\sigma}{n\,\cdot\,\text{e}^2}=2\,\cdot\,\text{v}_0\,\cdot\,\tau\approx(10^{-1}-10^1)\text{nm}\]
- And this is certainly too small!.
But before we discuss these results, let's see if they are actually true by doing an exercise:
Exercise 2.1-2: Derive numbers for v0, vD, τ, and l
Show that the claims made in the backbone text are actually true (for room temperature = 300 K). Use the following equations taken from the backbone
- For the average velocity v0 of a particle zooming around in the crystal:
\[\text{v}_0=\left(\frac{3\text{k}T}{m}\right)^{1/2}\]
- For the mean time τ between scattering:
\[\tau=\frac{\sigma\,\cdot\,m}{n\,\cdot\,\text{e}^2}\]
- For the drift velocity vD
\[\text{v}_D=-\frac{E\,\cdot\,\text{e}\,\cdot\,\tau}{m}\]
- For the minimal mean free path length lmin obtained for vD = 0:
\[l_\text{min}=2\,\cdot\,\text{v}_0\,\cdot\,\tau\]
Of course, you need numbers for the concentration n of the free carriers and for the specific conductivity σ
- Since we are essentially considering metals, you assume for a start that you have 1 free electron per atom if you want to find a number for n. Here are a few data needed for the calculation:
| Atom | Density [kg · m–3] |
Atomic weight × 1,66 · 10–27 kg |
Conductivity σ × 105 [Ω–1 · m–1] |
Conzentration Atoms n [m–3] ??? |
|---|---|---|---|---|
| Na | 970 | 23 | 2.4 | |
| Cu | 8.920 | 64 | 5.9 | |
| Au | 19.300 | 197 | 4.5 |
You may run into some trouble with the dimensions. Just look at conversions from, e.g. [eV] to [J], from Ω to V and A, and at the relations beween Volt, Ampere, Watts and Joule.
Solution 2.1-2: Derive numbers for v0, vD, τ, and l
First Task: Derive a number for v0 (at room temperature). We have
\[\text{v}_0=\left(\frac{3\underline{\color{blue}{\text{k}}}T}{\underline{\color{blue}{m}}}\right)^{1/2}= \left(\frac{8.6\,\cdot\,10^{-5}\,\cdot\,300}{9.1\,\cdot\,10^{-31}}\frac{\text{eV}\cdot\text{K}}{\text{K}\cdot\text{kg}}\right)^{1/2}= 1.68\cdot 10^{14}\cdot\left(\frac{\text{eV}}{\text{kg}}\right)^{1/2} \]
- The dimension "square root of eV/kg" does not look so good - for a velocity we would like to have m/s. In looking at the energies we equated kinetic energy with the classical dimension [kg · m2/s2] = [J] with thermal energy kT expressed in [eV]. So let's convert eV to J (use the link) and see if that solves the problem. We have 1 eV = 1,6 · 10–19 J = 1,6 · 10–19 kg · m2 · s–2 which gives us
\[ \text{v}_0=1.68\cdot10^{14}\cdot\left(\frac{1.6\cdot 10^{-19}\,\text{kg}\cdot\text{m}^2}{\text{kg}\cdot\text{s}^2}\right)^{1/2}=5.31\cdot 10^4\,\text{m/s}=1.91\cdot10^5\,\text{km/hr}\]
Possibly a bit surprising - those electrons are no sluggards but move around rather fast. Anyway, we have shown that a value of ≈ 104 m/s as postulated in the backbone is really OK.
- Of course, for T → 0, we would have v0→ 0 - which should worry us a bit ???? If instead of room temperature (T = 300 K) we would go to let's say 1200 K , we would just double the average speed of the electrons.
Second Task: Derive a number for τ. We have
\[\tau=\frac{\sigma\cdot m}{n\cdot \text{e}^2}\]
First we need some number for the concentration of free electrons per m3. For that we complete the table given, noting that for the number of atoms per m3 we have to divide the density by the atomic weight.
| Atom | Density [kg · m–3] |
Atomic weight × 1,66 · 10–27 kg |
Conductivity σ × 105 [Ω–1 · m–1] |
No. Atoms [m–3] × 10 28 |
|---|---|---|---|---|
| Na | 970 | 23 | 2,4 | 2,54 |
| Cu | 8.920 | 64 | 5,9 | 8,40 |
| Au | 19.300 | 197 | 4,5 | 5,90 |
- So let's take 5 · 1028 m–3 as a good order of magnitude guess for the number of atoms in a m3, and for a first estimate some average value σ = 5 · 105 [Ω–1 · m–1]. We obtain
\[\tau=\frac{5\cdot10^5\cdot9.1\cdot10^{-31}}{5\cdot10^{28}\cdot(1.6\cdot10^{-19})^2}\frac{\text{kg}\cdot\text{m}^3}{\Omega\cdot\text{m}\cdot\text{A}^2\cdot\text{s}^2}=3.55\cdot10^{-16}\frac{\text{kg}\cdot\text{m}^2}{\text{V}\cdot\text{A}\cdot\text{s}^2}\]
Well, somehow the whole thing would look much better with the unit [s]. So let's see if we can remedy the situation.
- Easy: Volts times Amperes equals Watts which is power, e.g. energy per time, with the unit [J · s–1] = kg · m2 · s–3. Insertion yields
\[\tau=1.42\cdot10^{-28}\frac{\text{kg}\cdot\text{m}^2\cdot\text{s}^3}{\text{kg}\cdot\text{m}^2\cdot\text{s}^2}=3.55\cdot10^{-16}\text{s}=0.35\,\text{fs}\]
The backbone thus is right again. The scattering time is in the order of femtosecond which is a short time indeed. Since all variables enter the equation linearly, looking at somewhat other carra ier densities (e.g. more than 1 electron per atom) or conductivities does not really change the general picture very much.
Third Task: Derive a number for vD . We have (for a field strength E = 100 V/m = 1 V/cm)
\[|{\text{v}_D}|=\frac{E\cdot\text{e}\cdot\tau}{m}=\frac{100\cdot1.6\cdot10^{-19}\cdot3.55\cdot10^{-16}}{9.1\cdot10^{-31}}\,\frac{\text{V}\cdot\text{C}\cdot\text{s}}{\text{m}\cdot\text{kg}}=6.24\cdot10^{-3}\, \frac{\text{V}\cdot\text{A}\cdot\text{s}^2}{\text{m}\cdot\text{kg}}\\ =6.24\cdot10^{-3}\, \frac{\text{kg}\cdot\text{m}^2\cdot\text{s}^2}{\text{kg}\cdot\text{m}\cdot\text{s}^3}= 6.24\cdot10^{-3}\,\text{m/s}=6.24\,\text{mm/s}\]
This is somewhat larger than the value given in the backbone text.
- However - a field strength of 1 V/cm applied to a metal is huge! Think about the current density j you would get if you apply 1 V to a piece of metal 1 cm thick.
- It is actually j = σ · E = 5 · 107 [Ω–1 · m–1] · 100 V/m = 5 · 109 A/m2 = 5 · 105 A/cm2!
- For a more "reasonable" current density of 103 A/cm2 we have to reduce E hundredfold and then end up with |vD| = 0,0624 mm/s - and that is slow indeed!
Fourth Task: Derive a number for l. We have
\[l_\text{min}=2\cdot\text{v}_0\cdot\tau=2\cdot5.31\cdot10^4\cdot3.55\cdot10^{-16}\, \text{m}=3.77\cdot10^7\,m=0.0377\,nm\]
- Right again! If we add the comparatively miniscule vD, nothing would change. Decreasing the temperature would lower l to eventually zero, or more precisely, to 2 · vD · τ and thus to a value far smaller than an atom.
Now to the important question: Why is a mean free path in the order of the size of an atom too small?
- Well, think about the scattering mechanisms. The distance between lattice defects is certainly much larger, and a phonon itself is "larger", too.
- Moreover, consider what happens at temperatures below room temperatures: l would become even smaller since v0 decreases - somehow this makes no sense.
It does not pay to spend more time on this. Whichever way you look at it, whatever tricky devices you introduce to make the approximations better (and physicists have tried very hard!), you will not be able to solve the problem: The mean free paths are never even coming close to what they need to be, and the conclusion which we will reach - maybe reluctantly, but unavoidably - must be:
There is no way to describe conductivity (in metals) with classical
physics!
Scattering and Mobility
Somewhere on the way, we have also indirectly found that the mobility µ as defined before is just another way to look at scattering mechanisms. Let's see why.
- All we have to do is to compare the equation for the conductivity from above with the master equation σ = q · n · µ.
This gives us immediately
\[\mu=\frac{\text{e}\cdot\tau}{m}\\\mu\approx\frac{\text{e}\cdot l}{2\cdot m \cdot\text{v}_0}\]
- In other words:
The decisive material property determining the mobility \(\mu\) is the
average time between scattering events or the mean free path between
those events.
- The mobility µ thus is a basic material property, well-defined even without electrical fields, and just another way to express the scattering processes taken place by a number.
In the equations above slumbers an extremely important aspect of semicoductor technology.
- In all electronic devices carriers have to travel some distance before a signal can be produced. A MOS transistor, for example, switches currents on or off between its "Source" and "Drain" terminal depending on what voltage is applied to its "Gate". Source and drain are separated by some distance lSD, and the "Drain" only "feels" the "on" state after the time it takes the carriers to run the distacne lSD.
- How long does that take if the voltage between Source and Drain is USD?
- Easy. If we know the mobility µ of the carriers, we now their (average) velocity vSD in the source-drain region, which by definition is vSD = µ · USD/lSD.
- The traveling time tSD between source and drain for obvious reasons defines roughly the maximum frequency fmax the transistor can hand, we have tSD = lSD / vSD or
\[t_{SD}=\frac{l_{SD}^2}{\mu\cdot\,U_{SD}}\approx\frac{1}{f_\text{max}}\]
- The maximum frequency of a MOS transistor thus is directly proportional to the mobiltiy of the carriers in the material it is made from (always provided there are no other limiting factors). And since we used a rather general argument, we should not be surprised that pretty much the same relation is also true for most electronic devices, not just MOS transistors.
- This is a momentous statement: We linked a prime material parameter, the material constant µ, to one of the most important parameters of electronic circuits. We would like µ to be as large as possible, of course, and now we know what to do about it!
A simple exercise is in order to see the power of this knowlegde:
Exercise 2.1-3: What does it take to build a 4 GHz Microprocessor?
A typical MOS transistor of 200x (x = 0 .... 5) vintage has a "gate length" (= distance between source an drain of about 0.5 µm and is run at about 3 V
- What is the mobility the material (= semiconductor) must have? Discuss the result for known mobility values and consider the following points
- Transistor speed = device speed ??
- Mobility range for a given material ??
- Could we have powerful PCs without micro- or nanotechnology ??
- How could you increase the speed for a given material
- In principal?
- Considering that there limits. e.g. to field strengths?
Solution 2.1-3: What does it take to build a 4 GHz Microprocessor?
First Task: What is the mobility the material (= semiconductor) must have? Discuss the result in considering the following points
- Transistor speed = device speed ???
- Mobility range for a given material ??
- Could we have powerful PCs without micro- or nanotechnology ??
The essential equation is
\[t_{SD}=\frac{l_{SD}^2}{\mu\cdot\,U_{SD}}\approx\frac{1}{f_\text{max}}\]
The necessary mobility thus is given by
\[\mu = \frac{l_{SD}^2}{t_{SD}\cdot\,U_{SD}}=\frac{f_\text{max}\cdot\,l_{SD}^2}{U_{SD}} = \frac{4\cdot10^9\cdot2.5\cdot10^{-13}}{3}\cdot\frac{\text{m}^2}{\text{s}\cdot\text{V}}= 0.33\cdot10^{-3}\frac{\text{m}^2}{\text{s}\cdot\text{V}}= 3.3\frac{\text{cm}^2}{\text{s}\cdot\text{V}}\]
What is the mobility of typical semiconductors? Finding values in the Net is not too difficult; if you just turn to the Hyperscript "Semiconductors" you should find this link
- Well, all "useful" semiconductors seem to be OK, their mobilities are much larger than what we need. But perhaps we are a little naive?
- Yes, we are! If a device combining some 10.000.000 transistors is to have a limit frequency of 4 Ghz, an individual transistor "obviously" must be much faster. If you don't see the obvious, think about the routing of many letters by the mail through a few million post offices (with different routes for every letter) and compare the individual and (average) total processing times.
- Bearing this in mind, mobilities of about a factor of 100 larger than the one we calculated do not look all that good anymore!
The mobility table in the link shows large variations in mobility for a given material - obviously µ is not really a material constant but somehow depends on the detailed structure.
- We do not need to understand the intricacies of that table - we already know that µ is directly proportional to the mean free path length l and thus somehow inversely proportional to defect densities.
- It is very clear, then, that for high-speed devices we need rather perfect crystals! So let's try to have single crystals, with no dislocations (or at least only small densities, meaning that the crystal must never plastically), and the minimum number of extrinsic and intrinsic point defects.
- Quite clear - but do you see the intrinsic problem? A more or less perfect crystal is not a device! To make a device from a crystal, we must do something to the crystal. And whatever you do to a perfect crystal - the result can only be a less perfect crystal!
- In other words: Making a device means to start with very good crystals and only induce the minimum of defects that is absolutely necessary.
Could we have 4 GHz without microelectronics?
- Well, take for lSD a value 100 times larger, and your highest frequency will be 10.000 times smaller - 400 kHz in the example. Of course, the 4 GHz of modern processors is not only determined by mobility values of the materials used, but the argument is nevertheless valid.
- So, without microelectronics (or by now nanoelectronics) life would by much different, because you can just about forget everything you do as a direct (and indirect!) present-day "user" of electronics. But would it be worse? The answer is a definite: Yes - it would be worse! Trust me - I have been there! It's not that long ago that 400 kHz was considered a pretty high frequency.
Second Task: How could you increase the speed for a given material
- In principal
- Considering that there limits. e.g. to field strength
- In principal it is simple: Make lSD smaller and / or USD larger.
- It is so simple, that you now should wonder, why it's not done immediately? Why not make a 40 GHz or 400 GHz microprocessor now - always, of course, only as far as it concerns the mobility?
Well, there are limits that are not so easily overcome. To name just two:
- Things are structured by "painting" with light. And just as much as you can't make a line thinner than than the size of your brush or pencil, you can't make structures smaller than the wavelength of the light you use, which is in the 0.5 µm range.
- Funny coincidence to the lSD we used, don't you think so?
OK, so we increase the voltage; let's say from 3 V to 300 V.
- This increases the field strength from 3/5 · 105 V/cm to 3/5 · 107 V/cm or 600.000 V/mm.
- In other words: A 1 mm thick layer of your material should be able to isolate a high-voltage cable carrying 600.000 V. Seems a bit strange, given the fact that they still hang lousy 300.000 V cables high up on poles to have many meters of air (a very good insulator) because otherwise you would have to use many cm of some really good insulating solid.
- To put it simple: no material withstands field strength of more than 10 MV/cm (give or take a few MV). If you try to exceed that value, you will get interesting and very loud fire works. Whenever mother nature tries it, we call it a thunderstorm.
- And only a few very good insulators will even come close to that number. Semiconductors, not being insulators, by necessity, can take far less. Our 60.000 V/cm are pretty much the limit. So forget about higher voltages, too.
Does this mean 4 GHz is the end of the line?
- No it's not. It just means it is not easy to go beyond. It take a lot of knowledge, understanding, and skills to make existing devices "better". It take highly qualified engineers and scientists to do the job. It takes what you will be in a few more years if you keep to ít!

