0.04: Memory

Memory

Memory Hierarchy

The CPU can only directly fetch instructions and data from cache memory, located directly on the processor chip. Cache memory must be loaded in from the main system memory (the Random Access Memory, or RAM). RAM however, only retains its contents when the power is on, so needs to be stored on more permanent storage.

We call these layers of memory the memory hierarchy

Table 3.1. Memory Hierarchy

Speed	Memory	Description
Fastest	Cache	Cache memory is memory actually embedded inside the CPU. Cache memory is very fast, typically taking only once cycle to access, but since it is embedded directly into the CPU there is a limit to how big it can be. In fact, there are several sub-levels of cache memory (termed L1, L2, L3) all with slightly increasing speeds.
	RAM	All instructions and storage addresses for the processor must come from RAM. Although RAM is very fast, there is still some significant time taken for the CPU to access it (this is termed latency). RAM is stored in separate, dedicated chips attached to the motherboard, meaning it is much larger than cache memory.
Slowest	Disk	We are all familiar with software arriving on a floppy disk or CDROM, and saving our files to the hard disk. We are also familiar with the long time a program can take to load from the hard disk -- having physical mechanisms such as spinning disks and moving heads means disks are the slowest form of storage. But they are also by far the largest form of storage.

The important point to know about the memory hierarchy is the trade offs between speed and size — the faster the memory the smaller it is. Of course, if you can find a way to change this equation, you'll end up a billionaire!

The reason caches are effective is because computer code generally exhibits two forms of locality

1. Spatial locality suggests that data within blocks is likely to be accessed together.

2. Temporal locality suggests that data that was used recently will likely be used again shortly.

This means that benefits are gained by implementing as much quickly accessible memory (temporal) storing small blocks of relevant information (spatial) as practically possible.

Cache in depth

Cache is one of the most important elements of the CPU architecture. To write efficient code developers need to have an understanding of how the cache in their systems works.

The cache is a very fast copy of the slower main system memory. Cache is much smaller than main memories because it is included inside the processor chip alongside the registers and processor logic. This is prime real estate in computing terms, and there are both economic and physical limits to its maximum size. As manufacturers find more and more ways to cram more and more transistors onto a chip cache sizes grow considerably, but even the largest caches are tens of megabytes, rather than the gigabytes of main memory or terabytes of hard disk otherwise common.

The cache is made up of small chunks of mirrored main memory. The size of these chunks is called the line size, and is typically something like 32 or 64 bytes. When talking about cache, it is very common to talk about the line size, or a cache line, which refers to one chunk of mirrored main memory. The cache can only load and store memory in sizes a multiple of a cache line.

Caches have their own hierarchy, commonly termed L1, L2 and L3. L1 cache is the fastest and smallest; L2 is bigger and slower, and L3 more so.

L1 caches are generally further split into instruction caches and data, known as the "Harvard Architecture" after the relay based Harvard Mark-1 computer which introduced it. Split caches help to reduce pipeline bottlenecks as earlier pipeline stages tend to reference the instruction cache and later stages the data cache. Apart from reducing contention for a shared resource, providing separate caches for instructions also allows for alternate implementations which may take advantage of the nature of instruction streaming; they are read-only so do not need expensive on-chip features such as multi-porting, nor need to handle handle sub-block reads because the instruction stream generally uses more regular sized accesses.

Figure 3.4. Cache Associativity

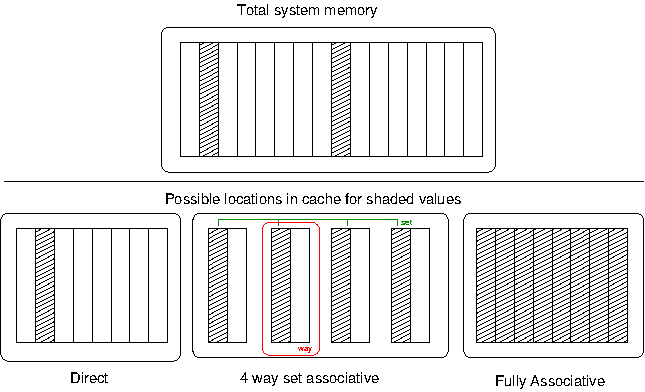
A given cache line may find a valid home in one of the shaded entries.

During normal operation the processor is constantly asking the cache to check if a particular address is stored in the cache, so the cache needs some way to very quickly find if it has a valid line present or not. If a given address can be cached anywhere within the cache, every cache line needs to be searched every time a reference is made to determine a hit or a miss. To keep searching fast this is done in parallel in the cache hardware, but searching every entry is generally far too expensive to implement for a reasonable sized cache. Thus the cache can be made simpler by enforcing limits on where a particular address must live. This is a trade-off; the cache is obviously much, much smaller than the system memory, so some addresses must alias others. If two addresses which alias each other are being constantly updated they are said to fight over the cache line. Thus we can categorise caches into three general types, illustrated in Figure 3.4, “Cache Associativity”.

• Direct mapped caches will allow a cache line to exist only in a singe entry in the cache. This is the simplest to implement in hardware, but as illustrated in Figure 3.4, “Cache Associativity” there is no potential to avoid aliasing because the two shaded addresses must share the same cache line.

• Fully Associative caches will allow a cache line to exist in any entry of the cache. This avoids the problem with aliasing, since any entry is available for use. But it is very expensive to implement in hardware because every possible location must be looked up simultaneously to determine if a value is in the cache.

• Set Associative caches are a hybrid of direct and fully associative caches, and allow a particular cache value to exist in some subset of the lines within the cache. The cache is divided into even compartments called ways, and a particular address could be located in any way. Thus an n-way set associative cache will allow a cache line to exist in any entry of a set sized total blocks mod n — Figure 3.4, “Cache Associativity” shows a sample 8-element, 4-way set associative cache; in this case the two addresses have four possible locations, meaning only half the cache must be searched upon lookup. The more ways, the more possible locations and the less aliasing, leading to overall better performance.

Once the cache is full the processor needs to get rid of a line to make room for a new line. There are many algorithms by which the processor can choose which line to evict; for example least recently used (LRU) is an algorithm where the oldest unused line is discarded to make room for the new line.

When data is only read from the cache there is no need to ensure consistency with main memory. However, when the processor starts writing to cache lines it needs to make some decisions about how to update the underlying main memory. A write-through cache will write the changes directly into the main system memory as the processor updates the cache. This is slower since the process of writing to the main memory is, as we have seen, slower. Alternatively a write-back cache delays writing the changes to RAM until absolutely necessary. The obvious advantage is that less main memory access is required when cache entries are written. Cache lines that have been written but not committed to memory are referred to as dirty. The disadvantage is that when a cache entry is evicted, it may require two memory accesses (one to write dirty data main memory, and another to load the new data).

If an entry exists in both a higher-level and lower-level cache at the same time, we say the higher-level cache is inclusive. Alternatively, if the higher-level cache having a line removes the possibility of a lower level cache having that line, we say it is exclusive. This choice is discussed further in the section called “Cache exclusivity in SMP systems”.

Cache Addressing

So far we have not discussed how a cache decides if a given address resides in the cache or not. Clearly, caches must keep a directory of what data currently resides in the cache lines. The cache directory and data may co-located on the processor, but may also be separate — such as in the case of the POWER5 processor which has an on-core L3 directory, but actually accessing the data requires traversing the L3 bus to access off-core memory. An arrangement like this can facilitate quicker hit/miss processing without the other costs of keeping the entire cache on-core.

Figure 3.5. Cache tags

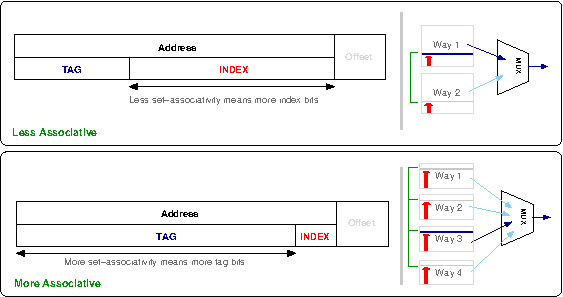
Tags need to be checked in parallel to keep latency times low; more tag bits (i.e. less set associativity) requires more complex hardware to achieve this. Alternatively more set associativity means less tags, but the processor now needs hardware to multiplex the output of the many sets, which can also add latency.

To quickly decide if an address lies within the cache it is separated into three parts; the tag and the index and the offset.

The offset bits depend on the line size of the cache. For example, a 32-byte line size would use the last 5-bits (i.e. 2⁵) of the address as the offset into the line.

The index is the particular cache line that an entry may reside in. As an example, let us consider a cache with 256 entries. If this is a direct-mapped cache, we know the data may reside in only one possible line, so the next 8-bits (2⁸) after the offset describe the line to check - between 0 and 255.

Now, consider the same 256 element cache, but divided into two ways. This means there are two groups of 128 lines, and the given address may reside in either of these groups. Consequently only 7-bits are required as an index to offset into the 128-entry ways. For a given cache size, as we increase the number of ways, we decrease the number of bits required as an index since each way gets smaller.

The cache directory still needs to check if the particular address stored in the cache is the one it is interested in. Thus the remaining bits of the address are the tag bits which the cache directory checks against the incoming address tag bits to determine if there is a cache hit or not. This relationship is illustrated in Figure 3.5, “Cache tags”.

When there are multiple ways, this check must happen in parallel within each way, which then passes its result into a multiplexor which outputs a final hit or miss result. As describe above, the more associative a cache is, the less bits are required for index and the more as tag bits — to the extreme of a fully-associative cache where no bits are used as index bits. The parallel matching of tags bits is the expensive component of cache design and generally the limiting factor on how many lines (i.e, how big) a cache may grow.