6.2.1: Some aspects about thermodynamics
- Page ID
- 78138
Before analyzing the characteristics and equations of the elements of the jet engine, let us briefly explain some basic concepts regarding thermodynamics (useful to understand what follows in the section). For more insight, the reader is referred to any undergraduate text book on thermodynamics.
The first law of the thermodynamics can be stated as follows:
\[\Delta E = Q + W.\label{eq6.2.1.1}\]
where \(E\) denotes de energy of the system, \(Q\) denotes de heat, and \(W\) denotes the work. In other words, an increase (decrease) in the energy of the system results in heat and work.
The energy of the system can be expressed as:
\[E = U + \dfrac{mV^2}{2} + mgz,\]
where \(U\) denotes the internal energy, the term \(\tfrac{mV^2}{2}\) denotes the kinetic energy, and the term \(mgz\) denotes the patential energy (with \(z\) being the altitude). In the case of a jet engine, \(z\) can be considered nearly constant, and the potential term thus neglected. Also, it is typical to use stagnation values for pressure and temperature of the gas, i.e., the values that the gas would have considering \(V = 0\) as already presented in Chapter 3. Under this assumption, the kinetic terms can be also neglected. Therefore, Equation (\(\ref{eq6.2.1.1}\)) can be expressed as:
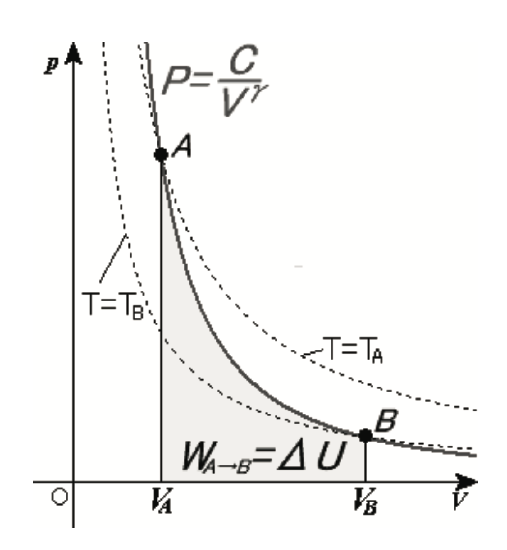
Figure 6.3: Sketch of an adiabatic process. © Yuta Aoki / Wikimedia Commons / CC-BY-SA-3.0.
\[\Delta U = Q + W.\]
Now, the work can be divided into two terms: mechanical work (\(W_{mech}\)) and work needed to expand/contract the gas (\(\Delta (PV)\)), i.e.,
\[W = W_{mech} + \Delta (PV).\]
Also, the enthalpy (\(h\)) of the system can be defined as: \(h = U + PV\). In sum, the energy equation (Equation (\(\ref{eq6.2.1.1}\))) can be expressed as follows:
\[\Delta h = Q + W_{mech}.\]
An increase of enthalpy can be expressed as follows:
\[\Delta h = c \cdot \Delta T;\]
where \(c\) is the specific heat of the gas and \(T\) is the temperature.
Moreover, we state now how the stagnation values are related to the real values:
\[h_t = h + \dfrac{V^2}{2};\]
\[p_t = p + \dfrac{1}{2} \cdot \rho \cdot V^2.\]
Notice that, if the process is adiabatic then \(Q = 0\), and thus the increase (decrease) in enthalpy is all turned into mechanical work. Adiabatic processes will be assumed for the stages at the compressor and turbine. Moreover, for an adiabatic process there are some relations between pressure and temperature for an ideal gas, i.e.,
\[P \cdot V^{\gamma} = constant \to \dfrac{p_a}{p_b} = \left (\dfrac{T_a}{T_b} \right )^{\tfrac{\gamma}{\gamma - 1}},\]
being \(a\) and \(b\) state conditions within the adiabatic process and \(\gamma\) the ratio of specific heats.2
2. This ratio is also referred to as heat capacity ratio or adiabatic index.


