11.5: Exercises
- Page ID
- 78407
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Consider an aircraft flying constant altitude \(h\) as illustrated in Figure 11.21. Assume the Earth is rotating at angular rate \(\vec{\Omega}_E = \Omega \cdot \vec{k}_E\), and there is no wind (calm conditions). Assume also the aircraft is equipped with a strap-down inertial navigation system. At time \(t\), accelerometers and gyroscopes are providing the following measurements:
- Angular velocity: \(\vec{W} = W_x \cdot \vec{i}_b + W_y \cdot \vec{j}_b + W_z \cdot \vec{k}_b \approx 0\).
- Body-Frame accelerations:18 \(\vec{a}_b = a_x \cdot \vec{i}_b + a_y \cdot \vec{j}_b + a_z \cdot \vec{k}_b\).
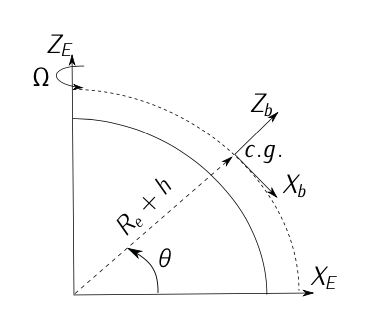
Figure 11.19: Inertial Navigation System (Exercise 3.1)
Consider:
- the aircraft is flying at speed \(\vec{V} = V \cdot \vec{i}_b\) at time \(t\).
- the angle \(\theta\) can be considered approximately constant.
Obtain:
- a symbolic expression of the acceleration terms \(a_x\), \(a_y\) and \(a_z\), identifying those that are due to the motion of the aircraft with respect to Earth and those that are due to inertial and gravitational effects.
- Substitute using the values below and provide the value (and direction) of the acceleration of the aircraft with respect to Earth:
\(\bullet\) \(\Omega = 1\ rev./day\).
\(\bullet\) \(W_x \approx 0; W_y \approx 0\)
\(\bullet\) \(a_x = 0.9831\ m/s^2; a_y = 0.0257\ m/s^2, a_z = -9.8269\ m/s^2\).
\(\bullet\) \(V = 250\ m/s; h = 11.000\ m\).
\(\bullet\) \(R_E = 6378\ km; g = 9.81\ m/s^2\).
\(\bullet\) \(\theta = 45\ deg\).
- Answer
-
Let us start saying that the absolute acceleration of a body is \(\vec{a}_i = \tfrac{d^2 \vec{r}}{dt^2}|_i\), and the velocity of a body is \(\vec{V}_i = \tfrac{d\vec{r}}{dt}|_i\), being frame \(i\) a inertial reference frame (e.g., a fixed star) and \(\vec{r}\) the radio vector and \(t\) the time.
Then, according the Newton's second law: \(m \cdot \tfrac{d^2 \vec{r}}{dt^2}|_i = \sum \vec{F}_{ext}\), being \(m\) the mass of the body and \(F_{ext}\) the external forces.
Using Coriolis formula, one has that the derivative on a generic vectorial magnitude (\(\vec{A}\)) in absolute terms (with respect to an inertial reference frame \(i\)) is equal to its derivative in relative terms (with respect to a non-inertial reference frame \(e\)) plus the vectorial product of the relative angular velocity of the two frames (\(\vec{w}_{ei}\)) and the generic vectorial magnitude \(\vec{A}\). In order words:
\[\dfrac{d\vec{A}}{dt}|_i = \dfrac{d\vec{A}}{dt}|_e + \vec{w}_{ei} \wedge \vec{A}\label{eq11.5.1} \]
Thus, we can say that:
\[\dfrac{d\vec{r}}{dt}|_i = \dfrac{d\vec{r}}{dt}|_e + \vec{w}_{ei} \wedge \vec{r} \nonumber \]
Taking derivatives:
\[\dfrac{d^2\vec{r}}{dt^2}|_i = \dfrac{d^2\vec{r}}{dt^2}|_e + \dfrac{d}{dt}[\vec{w}_{ei} \wedge \vec{r}] \nonumber \]
This results in:
\[\dfrac{d\vec{V}}{dt}|_i = \dfrac{d\vec{V}}{dt}|_e + \vec{w}_{ei} \wedge \vec{V}\label{eq11.5.4} \]
In other words, absolute terms are equal to relative terms plus Coriolis terms. We can also say that:
\[\dfrac{d^2\vec{r}}{dt^2}|_i = \dfrac{d}{dt} (\dfrac{d\vec{r}}{dt}|_i)|_i = \dfrac{d}{dt} (V + \vec{w}_{ei} \wedge \vec{r})|_i, \nonumber \]
which elaborating yields:
\[\dfrac{d^2\vec{r}}{dt^2}|_i = \dfrac{d\vec{V}}{dt}|_i + \dfrac{d}{dt}(\vec{w}_{ei} \wedge \vec{r})|_i\label{eq11.5.6} \]
Equation \ref{eq11.5.6} is also referred to as Navigation equation. We can apply Coriolis formula in \ref{eq11.5.1} to the first term of the right hand side in Equation \ref{eq11.5.6}, which yields \(\tfrac{d\vec{V}}{dt}|_e + \vec{w}_{ei} \wedge \vec{V}|_e\) as in Eq. \ref{eq11.5.4}, and to the second term of the right hand side in Equation \ref{eq11.5.6}, which yields \(\tfrac{d(\vec{w}_{ei} \wedge \vec{r})}{dt} + \vec{w}_{ei} \wedge (\vec{w}_{ei} \wedge \vec{r})\). Thus, Eq. \ref{eq11.5.6} results in:
\[\vec{a} |_i = \vec{a}|_e + 2 \cdot \vec{w}_{ei} \wedge \vec{V} + \vec{w}_{ei} \wedge (\vec{w}_{ei} \wedge \vec{r}),\label{eq11.5.7} \]
where \(\vec{V}\) and \(\vec{r}\) are magnitudes refereed to the non-inertial reference frame \(e\).
Equation \ref{eq11.5.7} is the well known composition of accelerations equation. In the context of navigation, it states that the absolute acceleration (with respect to an inertial reference frame i) is equal to the relative acceleration (with respect to a non-inertial reference frame e, typically the Earth) plus Coriolis effects (second term in the right hand side of \ref{eq11.5.7}) and centrifugal effects (third term in the right hand side of \ref{eq11.5.7}).
In the context of the problem under analysis, acceleration measured by the Inertial Measurement Unit are absolute (\(\vec{a}_b\)), including gravitational effects and inertial (Coriolis and centrifugal) terms. However, in order to further compute the position of the aircraft with respect to Earth (\(vec{a}_e\)), we are interested in relative acceleration, i.e., the acceleration of the body (the aircraft) with respect to Earth. In other words:
\[\vec{a}_b = \vec{a}_e + \vec{g} + Coriolis + Centrifugal \nonumber \]
Let’s now work on each of these terms. First, define the following vectors:
\[\vec{g} = -g \cdot \vec{k}_b \nonumber \]
\[\vec{w}_{ei} = \Omega \cdot \vec{k}_e \nonumber \]
\[\vec{r} = (R_e + h) \cdot \vec{k}_b \nonumber \]
\[\vec{V} = V \cdot \vec{i}_b \nonumber \]
Then, operating, one has:
\[Coriolis: 2 \Omega V \sin \theta \cdot \vec{j}_b \nonumber \]
\[Centrifugal: -\Omega^2 (R_e + h) \cos \theta \cdot \vec{i}_e \nonumber \]
\[Gravity: -g \cdot \vec{k}_b. \nonumber \]

Figure 11.20: Inertial Navigation System, including gravitational acceleration, Coriolis acceleration (\(2\Omega V\)), and centrifugal acceleration (\(\Omega^2 (R_e + h) \cos (\theta)\)).Please, see Figure 11.20.
We should project the centrifugal term into body-frame axis:
\[Centrifugal: -\Omega^2 (R_e + h) \cos \theta \cdot (\sin \theta \cdot \vec{i}_b + \cos \theta \cdot \vec{k}_b) \nonumber \]
Then, we can say:
\[a_x \cdot \vec{i}_b = (a_{ex} - \Omega^2 (R_e + h) \cos \theta \sin \theta) \cdot \vec{i}_b, \nonumber \]
\[a_y \cdot \vec{j}_b = (a_{ey} + 2\Omega V \sin \theta) \cdot \vec{j}_b, \nonumber \]
\[a_z \cdot \vec{k}_b = (a_{ez} - g - \Omega^2 (R_e + h) \cos^2 \theta) \cdot \vec{k}_b, \nonumber \]
where \(a_{ex}\), \(a_{ey}\), and \(a_{ez}\) are the accelerations of the aircraft with respect to Earth and \(a_x\), \(a_y\), and \(a_z\) are the absolute accelerations measured by the IMU.
Let us know particularize to the given values, resulting:
\[a_x \cdot \vec{i}_b = (a_{ex} - 0.0168941032554) \cdot \vec{i}_b, \nonumber \]
\[a_y \cdot \vec{j}_b = (a_{ey} + 0.0257111281143) \cdot \vec{j}_b, \nonumber \]
\[a_z \cdot \vec{k}_b = (a_{ez} - -9.82689410326) \cdot \vec{k}_b. \nonumber \]
With the measurements of the accelerometers being \(a_x = 0.9831\ m/s^2\), \(a_y = 0.0257\ m/s^2\), and \(a_z = -9.8269\ m/s^2\), respectively, one has: Let us know particularize to the given values, resulting:
\[a_{ex} \cdot \vec{i}_b \approx 1 \cdot \vec{i}_b \nonumber \]
\[a_{ey} \cdot \vec{j}_b \approx 0 \cdot \vec{j}_b \nonumber \]
\[a_{ez} \cdot \vec{k}_b \approx 0 \cdot \vec{k}_b \nonumber \]
Thus, the acceleration of the aircraft with respect to Earth, \(\vec{a}_e = 1 \cdot \vec{i}_b \ m/s^2\). This acceleration is the one that should be used to obtain the position of the aircraft via double integration (given certain initial conditions).

Figure 11.21: INS Sketch.
Consider an aircraft flying at constant altitude as illustrated in Figure 11.21. Assume the Earth can be considered flat, non-rotating,19 and there is no wind (calm conditions). Assume also the aircraft is equipped with a strap-down inertial navigation system. At time \(t\), accelerometers and gyroscopes are providing the following measurements:
- Angular velocity: \(\vec{w}_b = w \cdot \vec{k} \approx 0\).
- Body-Frame forces: \(\vec{f}_b = (f_{bx} \cdot \vec{i}_b, f_{by} \cdot \vec{j}_b)\).
Given the following initial conditions:
- initial heading/track angle: \(\theta_0\);
- initial time: \(t_0\);
- initial position: \(\vec{r}_0 = (x_0 \cdot \vec{i}_e, y_0 \cdot \vec{j}_e)\);
- initial velocity: \(\vec{v}_0 = (v_0 \cdot \vec{i}_b, 0 \cdot \vec{j}_b)\);
Calculate:
- Position of the aircraft at time \(t\).
- Answer
-
First of all, the reader should notice that by assuming a non-rotating Earth, we are not considering Inertial (Coriolis and Centrifugal) terms. Also, because the movement is considered horizontal, gravity does not play any role in this problem. Of course, a realistic Inertial Navigation problem would require to conduct the analysis in the previous exercise. For the sake of simplicity, we focus herein on integrating the accelerations to obtain the position (something missing in the previous exercise).
Notice that \(\vec{w} = \dot{\theta}\), being \(\theta\) an arbitrary angle between a fixed direction, e.g., \(\vec{i}_e\), and the track of the aircraft, i.e., \(\vec{i}_b\).
Thus we can obtain the variation of \(\theta\) over time \(\theta (t)\) by simply integrating the flowing equation:
\[\int_{\theta_0}^{\theta} d\theta = \int_{t_0}^{t} w(t) dt \to \theta (t).\label{eq11.5.26} \]
Now, since the measurement of the gyroscope can be approximated to zero, i.e., \(\vec{w} \approx 0\), Equation \(\ref{eq11.5.26}\) yields:
\[\theta = \theta_0. \nonumber \]
The strap-down accelerometers provide measurements of absolute forces in the body frame axis that can be readily (under the conditions herein assumed) transformed in accelerations, i.e., \(\vec{a}_b = (a_{bx} \cdot \vec{i}_b, a_{by} \cdot \vec{j}_b)\).
Now, in order to expressed the absolute acceleration in the Earth reference frame, we have to simply apply a rotation:
\[\begin{bmatrix} \vec{a}_{ex} \\ \vec{a}_{ey} \end{bmatrix} = \begin{bmatrix} \cos \theta_0 & -\sin \theta_0 \\ \sin \theta_0 & \cos \theta_0 \end{bmatrix} \cdot \begin{bmatrix} \vec{a}_{bx} \\ \vec{a}_{by} \end{bmatrix} \nonumber \]
We now that:
\[\dfrac{d\vec{V}}{dt} = \vec{a}; \nonumber \]
\[\dfrac{d\vec{r}}{dt} = d \vec{V}. \nonumber \]
By integrating once, we obtain:
\[v_x = v_0 + (a_{xb} \cdot \cos \theta_0 - a_{yb} \cdot \sin \theta_0) \cdot t \nonumber \]
\[v_y = (a_{yb} \cdot \sin \theta_0 + a_{xb} \cdot \cos \theta_0) \cdot t \nonumber \]
By integrating twice, we obtain:
\[x = x_0 + v_0 \cdot t + (a_{xb} \cdot \cos \theta_0 - a_{yb} \cdot \sin \theta_0 ) \cdot \dfrac{t^2}{2} \nonumber \]
\[y = y_0 + (a_{yb} \cdot \sin \theta_0 + a_{xb} \cdot \cos \theta_0) \cdot \dfrac{t^2}{2} \nonumber \]
Notice that \(t\) is supposed to be sufficiently small (indeed, equivalent to the frequency of measurement) such that measurements can be considered constant along the time interval.
18. for the sake of simplicity, we assume accelerometers directly provide accelerations after having measured forces and having done the appropriate transformations.
19. one can assume both centrifugal and Coriolis terms are neglectable in the formula that relates absolute and relative acceleration. In other words, absolute and relative accelerations can be consider identical. Notice that this is true herein because we have considered the Earth non-rotating.


