8.3: Non-linear Optimization
- Page ID
- 22410
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Various conditions and situations are not adequately described using linear systems. In this case, nonlinear optimization may be applied. Unlike linear optimization, the optimal operating condition does not exist at the boundaries.
Quadratic Optimization
\[f(x)=c-x^{T} b+\frac{1}{2} x^{T} A x\nonumber \]
To optimize, it is necessary to find when the gradient of f is equal to zero.
\[\nabla f(x)=0\nonumber \]
\[\nabla f(x)=b-A x\nonumber \]
\[x_{*}=A^{-1} b\nonumber \]
It may be possible to solve the optimal 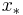 by a linear equation, approximated by a Taylor series.
by a linear equation, approximated by a Taylor series.
\[f\left(x_{*}\right)=f(x)+\left(x_{*}-x\right)^{\prime} \nabla f(x)+\frac{1}{2}\left(x_{*}-x\right)^{\prime} \nabla \nabla f(x)\left(x_{*}-x\right)+\ldots\nonumber \]
Iterative Methods
When direct methods cannot solve the equation (i.e. A is not symmetric positive definite), iterative methods are possible [1].
By starting with an initial guess of 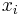 , an algorithm may lead to a
, an algorithm may lead to a 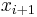 that better satisfies the equation. Through iteration, theoretically,
that better satisfies the equation. Through iteration, theoretically, 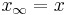 .
.
Applications
- Finance: Portfolio optimization
- Businesses: Optimize inventory
- Engineering: Rigid body dynamics
- Biochemistry: Kinetic modeling [2]
Example: Typical Nonlinear 3d Curves
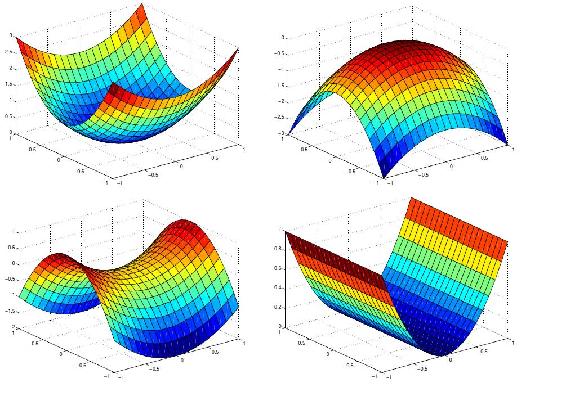
(Image from [1])
As observed, the optimal condition does not necessarily exist at the boundary of the curve.
Example: Quadratic Optimization
\[f(x)=\vec{c}^{T} \vec{x}+\frac{1}{2} \vec{x}^{T} Q \vec{x}\nonumber \]
where
\[\vec{c}^{T}=\left(c_{1}, c_{2}, \ldots, c_{n}\right)\nonumber \]
\[\vec{x}^{T}=\left(x_{1}, x_{2}, \ldots, x_{n}\right)\nonumber \]
For a quadratic system, \(n=2\), thus, \(Q\) (the quadratic term constant) is defined as a symmetric matrix as follows.
\[Q=\left[\begin{array}{ll}
Q_{1} & Q_{3} \\
Q_{3} & Q_{2}
\end{array}\right]\nonumber \]
Thus, multiplying out the \(f\),
\[f(x)=\left(c_{1} x_{1}+c_{2} x_{2}\right)+\frac{1}{2}\left(Q_{1} x_{1}^{2}+2 Q_{3} x_{1} x_{2}+Q_{2} x_{2}^{2}\right)\nonumber \]
References
- Lippert, Ross A. "Introduction to non-linear optimization." D.E. Shaw Research, February 25, 2008. http://www.mit.edu/~9.520/spring08/Classes/optlecture.pdf
- Mendes, Pedro and Kell, Douglas B. "Non-linear optimization of biochemical pathways: application to metabolic engineering and parameter estimation." Journal of Bioinformatics, Volume 14, 869-883. 1998.
- "Introduction to Non-linear optimization." Georgia Institute of Technology Systems Realization Laboratory. www.srl.gatech.edu/education/ME6103/NLP-intro.ppt


