13.12: Factor analysis and ANOVA
- Page ID
- 22533
First invented in the early 1900s by psychologist Charles Spearman, factor analysis is the process by which a complicated system of many variables is simplified by completely defining it with a smaller number of "factors." If these factors can be studied and determined, they can be used to predict the value of the variables in a system. A simple example would be using a person's intelligence (a factor) to predict their verbal, quantitative, writing, and analytical scores on the GRE (variables).
Analysis of variance (ANOVA) is the method used to compare continuous measurements to determine if the measurements are sampled from the same or different distributions. It is an analytical tool used to determine the significance of factors on measurements by looking at the relationship between a quantitative "response variable" and a proposed explanatory "factor." This method is similar to the process of comparing the statistical difference between two samples, in that it invokes the concept of hypothesis testing. Instead of comparing two samples, however, a variable is correlated with one or more explanatory factors, typically using the F-statistic. From this F-statistic, the P-value can be calculated to see if the difference is significant. For example, if the P-value is low (P-value<0.05 or P-value<0.01 - this depends on desired level of significance), then there is a low probability that the two groups are the same. The method is highly versatile in that it can be used to analyze complicated systems, with numerous variables and factors. In this article, we will discuss the computation involved in Single-Factor, Two-Factor: Without Replicates, and Two-Factor: With Replicates ANOVA. Below, is a brief overview of the different types of ANOVA and some examples of when they can be applied.
Overview and Examples of ANOVA Types
ANOVA Types
Single-Factor ANOVA (One-Way):
One-way ANOVA is used to test for variance among two or more independent groups of data, in the instance that the variance depends on a single factor. It is most often employed when there are at least three groups of data, otherwise a t-test would be a sufficient statistical analysis.
Two-Factor ANOVA (Two-Way):
Two-way ANOVA is used in the instance that the variance depends on two factors. There are two cases in which two-way ANOVA can be employed:
- Data without replicates: used when collecting a single data point for a specified condition
- Data with replicates: used when collecting multiple data points for a specified condition (the number of replicates must be specified and must be the same among data groups)
When to Use Each ANOVA Type
- Example: There are three identical reactors (R1, R2, R3) that generate the same product.
- One-way ANOVA: You want to analyze the variance of the product yield as a function of the reactor number.
- Two-way ANOVA without replicates: You want to analyze the variance of the product yield as a function of the reactor number and the catalyst concentration.
- Two-way ANOVA with replicates: For each catalyst concentration, triplicate data were taken. You want to analyze the variance of the product yield as a function of the reactor number and the catalyst concentration.
ANOVA is a Linear Model
Though ANOVA will tell you if factors are significantly different, it will do so according to a linear model. ANOVA will always assumes a linear model, it is important to consider strong nonlinear interactions that ANOVA may not incorporate when determining significance. ANOVA works by assuming each observation as overall mean + mean effect + noise. If there are non-linear relationship between these (for example, if the difference between column 1 and column 2 on the same row is that column2 = column1^2), then there is the chance that ANOVA will not catch it.
Key Terms
Before further explanation, please review the terms below, which are used throughout this Wiki.

Comparison of Sample Means Using the F-Test
The F-Test is the ratio of the sample variances. The F-statistic and the corresponding F-Test are used in single-factor ANOVA for purposes of hypothesis testing.
Null hypothesis (Ho): all sample means arising from different factors are equal
Alternative hypothesis (Ha): the sample means are not all equal
Several assumptions are necessary to use the F-test:
- The samples are independent and random
- The distribution of the response variable is a normal curve within each population
- The different populations may have different means
- All populations have the same standard deviation
Introduction to the F-Statistic
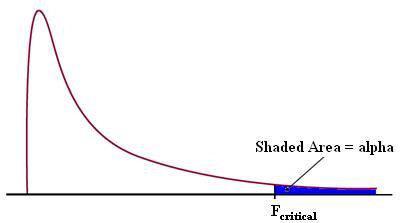
The F-statistic is the ratio of two variance estimates: the variance between groups divided by the variance within groups. The larger the F-statistic, the more likely it is that the difference between samples is due to the factor being tested, and not just the natural variation within a group. A standardized table can be used to find Fcritical for any system. Fcritical will depend on alpha, which is a measure of the confidence level. Typically, a value of alpha = 0.05 is used, which corresponds to 95% confidence. If Fobserved > Fcritical, we conclude with 95% confidence that the null hypothesis is false. For an explanation of how to read an F-Table, see Interpreting the F-statistic (below). In a similar manner, F tables can also be used to determine the p-value for a given data set. The p-value for a given data set is the probability that you could obtain this data set if the null hypothesis were true: that is, if the results were strictly due to chance. When Ho is true, the F-statistic has an F distribution.
F-Distributions
The F-distribution is important to ANOVA, because it is used to find the p-value for an ANOVA F-test. The F-distribution arises from the ratio of two Chi squared distributions. Thus, this family has a numerator and denominator degrees of freedom. (For information on the Chi squared test, click here.) Every function of this family has a a skewed distribution and minimum value of zero.
Figure 1 - F distribution with alpha and Fcritical indicated
Single-Factor Analysis of Variance
In the case of single-factor analysis, also called single classification or one-way, a factor is varied while observing the result on the set of dependent variables. These dependent variables belong to a specific related set of values and hence, the results are expected to be related.
This section will describe some of the computational details for the F-statistic in one-way ANOVA. Although these equations provide insight into the concept of analysis of variance and how the F-test is constructed, it is not necessary to learn formulas or to do this analysis by hand. In practice, computers are always used to do one-way ANOVA
Setting up an Analysis of Variance Table
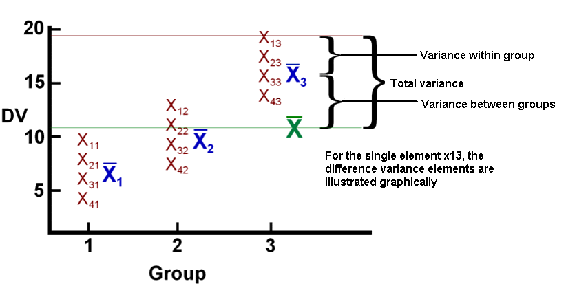
The fundamental concept in one-way analysis of variance is that the variation among data points in all samples can be divided into two categories: variation between group means and variation between data points in a group. The theory for analysis of variance stems from a simple equation, stating that the total variance is equal to the sum of the variance between groups and the variation within groups –
Total variation = variation between groups + variation within groups
An analysis of variance table is used to organize data points, indicating the value of a response variable, into groups according to the factor used in each case. For example, Table 1 is an ANOVA table for comparing the amount of weight lost over a three month period by dieters on various weight-loss programs.
| Program 1 | Program 2 | Program 3 |
|---|---|---|
| 7 | 9 | 15 |
| 9 | 11 | 12 |
| 5 | 7 | 18 |
| 7 |
A reasonable question is, can the type of program (a factor) be used to predict the amount of weight a dieter would lose on that program (a response variable)? Or, in other words, is any one program superior to the others?
Measuring Variation Between Groups
The variation between group means is measured with a weighted sum of squared differences between the sample means and the overall mean of all the data. Each squared difference is multiplied by the appropriate group sample size, ni, in this sum. This quantity is called sum of squares between groups or SS Groups.
\[\text { SSGroups }=n_{1}\left(x_{1}-x\right)^{2}+n_{2}\left(x_{2}-x\right)^{2}+\ldots+n_{k}\left(x_{k}-x\right)^{2}=\sum_{\text {yrсups }} n_{j}\left(\bar{x}_{j j}-\bar{x}^{\prime 2}\right.\nonumber \]
The numerator of the F-statistic for comparing means is called the mean square between groups or MS Groups, and it is calculated as -
\[\text { MSGroups }=\frac{\text { SSGroups }}{k-1}\nonumber \]
Measuring Variation Within Groups
To measure the variation among data points within the groups, find the sum of squared deviations between data values and the sample mean in each group, and then add these quantities. This is called the sum of squared errors, SSE, or sum of squares within groups.
\[S S E=\left(n_{1}-1\right) s_{1}^{2}+\left(n_{2}-1\right) s_{2}^{2}+\ldots+\left(n_{k}-1\right) s_{k}^{2}=\sum_{\text {allgroups }}\left(n_{j}-1\right) s_{j}^{2}\nonumber \]
where
\[s_{j}^{2}=\sum_{\text {groupj }} \frac{\left(x_{i j}-\bar{x}_{j}\right)^{2}}{n_{j}-1}=\nonumber \]
and is the variance within each group.
The denominator of the F-statistic is called the mean square error, MSE, or mean squares within groups. It is calculated as
\[M S E=\frac{S S E}{N-k}=\frac{\left(n_{1}-1\right) s_{1}^{2}+\left(n_{2}-1\right) s_{2}^{2}+\ldots+\left(n_{k}-1\right) s_{k}^{2}}{n_{1}+n_{2}+\ldots+n_{k}-k}\nonumber \]
MSE is simply a weighted average of the sample variances for the k groups. Therefore, if all ni are equal, MSE is simply the average of the k sample variances. The square root of MSE (sp), called the pooled standard deviation, estimates the population standard deviation of the response variable (keep in mind that all of the samples being compared are assumed to have the same standard deviation σ).
Measuring the Total Variation
The total variation in all samples combined is measured by computing the sum of squared deviations between data values and the mean of all data points. This quantity is referred to as the total sum of squares or SS Total. The total sum of squares may also be referred to as SSTO. A formula for the sum of squared differences from the overall mean is
\[\text { SSTotal }=\sum_{\text {values }}\left(x_{i j}-\bar{x}\right)^{2}\nonumber \]
where xij represents the jth observation within the ith group, and 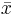 is the mean of all observed data values. Finally, the relationship between SS Total, SS Groups, and SS Error is
is the mean of all observed data values. Finally, the relationship between SS Total, SS Groups, and SS Error is
SS Total = SS Groups + SS Error
Overall, the relationship between the total variation, the variation between groups, and the variation within a group is illustrated by Figure 2.
A general table for performing the one-way ANOVA calculations required to compute the F-statistic is given below
| Source | Degrees of Freedom | Sum of Squares | Mean Sum of Squares | F-Statistic |
|---|---|---|---|---|
| Between groups | k-1 | 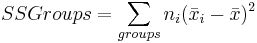 |
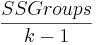 |
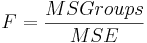 |
| Within groups (error) | N-k | 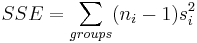 |
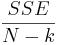 |
|
| Total | N-1 | 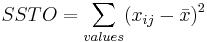 |
Interpreting the F-statistic
Once the F-statistic has been found, it can be compared with a critical F value from a table, such as this one: F Table. This F table is calculated for a value of alpha = 0.05, indicating a 95% confidence level. This means that if Fobserved is larger than Fcritical from the table, then we can reject the null hypothesis and say with 95% confidence that the variance between groups is not due to random chance, but rather due to the influence of a tested factor. Tables are also available for other values of alpha and can be used to find a more exact probability that the difference between groups is (or is not) caused by random chance.
Finding the Critical F value
In this F Table, the first row of the F table is the number of degrees of between groups (number of groups - 1), and the first column is the number of degrees of freedom within groups (total number of samples - number of groups).
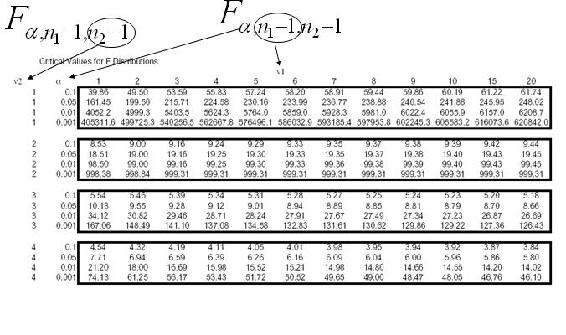
For the diet example in Table 1, the degree of freedom between groups is (3-1) = 2 and and the degree of freedom within groups is (13-3) = 10. Thus, the critical F value is 4.10.
Computing the 95% Confidence Interval for the Population Means
It is useful to know the confidence interval at which the means of the different groups are reported. The general formula for calculating a confidence interval is 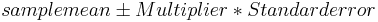 . Because it is assumed that all populations have the same standard deviation
. Because it is assumed that all populations have the same standard deviation 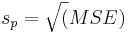 can be used to estimate the standard deviation within each group. Although the population standard deviation is assumed to be the same, the standard error and the multiplier may be different for each group, due to differences in group size and degrees of freedom. The standard error of a sample mean is inversely proportional to the square root of the number of data points within the sample. It is calculated as
can be used to estimate the standard deviation within each group. Although the population standard deviation is assumed to be the same, the standard error and the multiplier may be different for each group, due to differences in group size and degrees of freedom. The standard error of a sample mean is inversely proportional to the square root of the number of data points within the sample. It is calculated as 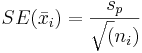 . The multiplier is determined using a t-distribution where the degrees of freedom are calculated as df = N-k. Therefore,Insertformulahere the confidence interval for a population mean is
. The multiplier is determined using a t-distribution where the degrees of freedom are calculated as df = N-k. Therefore,Insertformulahere the confidence interval for a population mean is  . More details on confidence intervals can be found in Comparison of two means
. More details on confidence intervals can be found in Comparison of two means
An example for using factor analysis is the following:
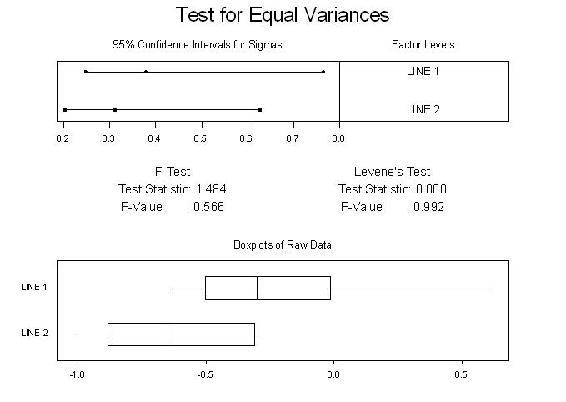
You have two assembly lines. Suppose you sample 10 parts from the two assembly lines. Ho: s12 = s2x2 Ha: variances are not equal Are the two lines producing similar outputs? Assume a=0.05 F.025,9,9 = 4.03 F1-.025,9,9 = ?
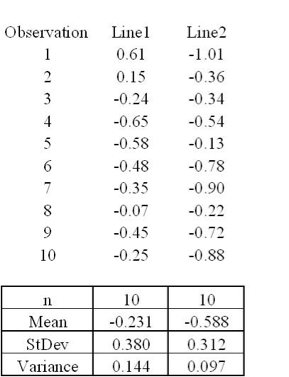
Are variances different?

How would we test if the means are different?
Two-Factor Analysis of Variance
A two factor or two-way analysis of variance is used to examine how two qualitative categorical variables (male/female) affect the mean of a quantitative response variable. For example, a psychologist might want to study how the type and volume of background music affect worker productivity. Alternatively, an economist maybe be interested in determining the affect of gender and race on mean income. In both of these examples, there is interest in the effect of each separate explanatory factor, as well as the combined effect of both factors.
Assumptions
In order to use the two-way ANOVA, the following assumptions are required:
- Samples must be independent.
- Population variances must be equal.
- Groups must have same sample size. The populations from which the samples were obtained must be normally distributed (or at least approximately so).
- The null hypothesis is assumed to be true.
The null hypothesis is as follows:
- The population means for the first factor have to be equal. This is similar to the one-way ANOVA for the row factor.
- The population means for the second factor must also be equal. This is similar to the one-way ANOVA for the column factor.
- There isn’t an interaction between the two factors. This is similar to performing an independence test using contingency tables.
More simply, the null hypothesis implies that the populations are all similar and any differences in the populations are caused by chance, not by the influence of a factor. After carrying out two-way ANOVA it will be possible to analyze the validity of this assumption.
Terms Used in Two-Way ANOVA
The interaction between two factors is the most unique part of a two-way analysis of variance problem. When two factors interact, the effect on the response variable depends on the value of the other factor. For example, the statement being overweight caused greater increases in blood pressure for men than women describes an interaction. In other words, the effect of weight (factor) on blood pressure (response) depends on gender (factor).
The term main effect is used to describe the overall effect of a single explanatory variable. In the music example, the main effect of the factor "music volume" is the effect on productivity averaged over all types of music. Clearly, the main effect may not always be useful if the interaction is unknown.
In a two-way analysis of variance, three F-statistics are constructed. One is used to test the statistical significance of the interaction, while the other two are used to test the significance of the two separate main effects. The p-value for each F-statistic is also reported--a p-value of <.05 is usually used to indicate significance. When an F-factor is found to have statistical significance, it is considered a main effect. The p-value is also used as an indicator to determine if the two factors have a significant interaction when considered simultaneously. If one factor depends strongly on the other, the F-statistic for the interaction term will have a low p-value. An example output of two-way analysis of variance of restaurant tip data is given in Table 4.
| Source | DF | Adj SS | Adj MS | F-Statistic | P-Value |
|---|---|---|---|---|---|
| Message | 1 | 14.7 | 14.7 | .13 | .715 |
| Sex | 1 | 2602.0 | 2602.0 | 23.69 | 0.00 |
| Interaction | 1 | 438.7 | 438.7 | 3.99 | .049 |
| Error | 85 | 9335.5 | 109.8 | ||
| Total | 88 | 12407.9 |
In this case, the factors being studied are sex (male or female) and message on the receipt ( :-) or none). The p-values in the last column are the most important information contained in this table. A lower p-value indicates a higher level of significance. Message has a significance value of .715. This is much greater than .05, the 95% confidence interval, indicating that this factor has no significance (no strong correlation between presence of message and amount of tip). The reason this occurs is that there is a relationship between the message and the sex of the waiter. The interaction term, which was significant with a value of p= 0.049, showed that drawing a happy face increased the tip for women but decreased it for men. The main effect of waiter sex (with a p-value of approximately 0) shows that there is a statistical difference in average tips for men and women.
Two-Way ANOVA Calculations
Like in one-way ANOVA analysis the main tool used is the square sums of each group. Two-way ANOVA can be split between two different types: with repetition and without repetition. With repetition means that every case is repeated a set number of times. For the above example that would mean that the :-) was given to females 10 times and males 10 times, and no message was given to females 10 times and males 10 times
Using the SS values as a start the F-statistics for two-way ANOVA with repetition are calculated using the chart below where a is the number of levels of main effect A, b is the number of levels of main effect B, and n is the number of repetitions.
| Source | SS | DF | Adj MS | F-Statistic |
|---|---|---|---|---|
| Main Effect A | From data given | a-1 | SS/df | MS(A)/MS(W) |
| Main Effect B | From data given | b-1 | SS/df | MS(B)/MS(W) |
| Interaction Effect | From data given | (a-1)(b-1) | SS/df | MS(A*B)/MS(W) |
| Within | From data given | ab(n-1) | SS/df | |
| Total | sum of others | abn-1 |
Without repetition means there is one reading for every case. For example is you were investigating whether or not difference in yield are more significant based on the day the readings were taken or the reactor that the readings were taken from you would have one reading for Reactor 1 on Monday, one reading for Reactor 2 on Monday etc... The results for two-way ANOVA without repetition is slightly different in that there is no interaction effect measured and the within row is replaced with a similar (but not equal) error row. The calculations needed are shown in the table below.
| Source | SS | DF | MS | F-Statistic |
|---|---|---|---|---|
| Main Effect A | From data given | a-1 | SS/df | MS(A)/MS(E) |
| Main Effect B | From data given | b-1 | SS/df | MS(B)/MS(E) |
| Error | From data given | (a-1)(b-1) | SS/df | |
| Total | sum of others | ab-1 |
These calculations are almost never done by hand. In this class you will usually use Excel or Mathematica to create these tables. Sections describing how to use these programs are found later in this chapter.
Other Methods of Comparison
Unfortunately, the conditions for using the ANOVA F-test do not hold in all situations. In this section, several other methods which do not rely on equal population standard deviations or normal distribution. It is important to realize that no method of factor analysis is appropriate if the data given is not representative of the group being studied.
Hypotheses About Medians
In general, it is best construct hypotheses about a population median, rather than the mean. Using the median accounts for the sample being skewed based on extreme outliers. Median hypotheses should also be used for dealing with ordinal variables (variables which are described only as being higher or lower than one other and do not have a precise value). When several populations are compared, the hypotheses are stated as -
H0: Population medians are equal
Ha: Population medians are not all equal
Kruskal-Wallis Test for Comparing Medians
The Kruskal-Wallis Test provides a method of comparing medians by comparing the relative rankings of data in the observed samples. This test is therefore referred to as a rank test or non-parametric test because the test does not make any assumptions about the distribution of data.
To conduct this test, the values in the total data set are first ranked from lowest to highest, with 1 being lowest and N being highest. The ranks of the values within each group are averaged, and the test statistic measures the variation among the average ranks for each group. A p-value can be determined by finding the probability that the variation among the set of rank averages for the groups would be as large or larger as it is if the null hypothesis is true. More information on the Kruskal-Wallis test can be found [here].
Mood's Median Test for Comparing Medians
Another nonparametric test used to compare population medians is Mood's Median Test. Also called the Sign Scores Test, this test involves multiple steps.
1. Calculate the median (M) using all data points from every group in the study
2. Create a contingency table as follows
| A | B | C | Total | |
|---|---|---|---|---|
| Number of values greater than M | ||||
| Number of values less than or equal to M |
3. Calculate the expected value for each data set using the following formula:
\[\text { expected }=\frac{(\text { rowtotal })(\text { columntotal })}{\text { grandtotal }}\nonumber \]
4. Calculate the chi-square value using the following formula
\[\chi=\frac{(\text { actual - expected })^{2}}{\text { expected }}\nonumber \]
A chi-square statistic for two-way tables is used to test the null hypothesis that the population medians are all the same. The test is equivalent to testing whether or not the two variables are related.
ANOVA and Factor Analysis in Process Control
ANOVA and factor analysis are typically used in process control for troubleshooting purposes. When a problem arises in a process control system, these techniques can be used to help solve it. A factor can be defined as a single variable or simple process that has an effect on the system. For example, a factor can be temperature of an inlet stream, flow rate of coolant, or the position of a specific valve. Each factor can be analyzed individually to determine the effect that changing the input has on the process control system as a whole. The input variable can have a large, small, or no effect on what is being analyzed. The amount that the input variable affects the system is called the “factor loading”, and is a numerical measure of how much a specific variable influences the system or the output variable. In general, the larger the factor loading is for a variable the more of an affect that it has on the output variable.
A simple equation for this would be:
Output = f1 * input1 + f2 * input2 + ... + fn * inputn
where fn is the factor loading for the nth input.
Factor analysis is used in this case study to determine the fouling in an alcohol plant reboiler. This article provides some additional insight as to how factor analysis is used in an industrial situation.
Using Mathematica to Conduct ANOVA
Mathematica can be used for one-way and two-way factor anaylses. Before this can be done, the ANOVA package must be loaded into Mathematica using the following command:
Needs["ANOVA`"]
Once this command is executed, the 'ANOVA' command can be utilized.
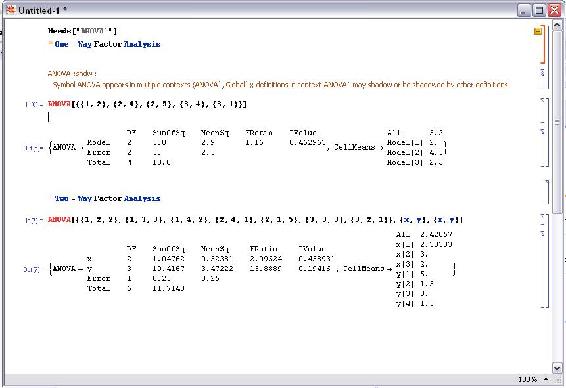
One-Way Factor Analysis
The basic form of the 'ANOVA' command to perform a one-way factor analysis is as follows:
ANOVA[data]
An example set of data with five elements would look like:
ANOVA[
Callstack:
at (Bookshelves/Industrial_and_Systems_Engineering/Chemical_Process_Dynamics_and_Controls_(Woolf)/13:_Statistics_and_Probability_Background/13.12:_Factor_analysis_and_ANOVA), /content/body/div[8]/div[1]/p[3]/span, line 1, column 2
An output table that includes the degrees of freedom, sum of the squares, mean sum of the squares, F-statistic, and the P-value for the model, error, and total will be displayed when this line is executed. A list of cell means for each model will be displayed beneath the table.
Two-Way Factor Analysis
The basic form of the 'ANOVA' command to perform a two-way factor analysis is as follows:
ANOVA[data, model, vars]
An example set of data with seven elements would look like:
ANOVA[
Callstack:
at (Bookshelves/Industrial_and_Systems_Engineering/Chemical_Process_Dynamics_and_Controls_(Woolf)/13:_Statistics_and_Probability_Background/13.12:_Factor_analysis_and_ANOVA), /content/body/div[8]/div[2]/p[3]/span, line 1, column 2
An output table will appear similar to the one that is displayed in the one-way analysis except that there will be a row of statistics for each variable (i.e. x,y).
ANOVA in Microsoft Excel 2007
In order to access the ANOVA data analysis tool, install the package:
- Click on the Microsoft Office button (big circle with office logo)
- Click 'Excel Options'
- Click 'Add-ins' on the left side
- In the manage drop-down box at the bottom of the window, select 'Excel Add-ins'
- Click 'Go...'
- On the Add-Ins window, check the Analysis ToolPak box and click 'OK'
To use this package:
- Click on the 'Data' tab and select 'Data Analysis'
- Choose the desired ANOVA type- 'Anova: Single Factor', 'Anova: Two Factor with Replication', or 'Anova: Two Factor without Replication'(see note below for when to use replication)
- Select the desired data points including data labels at top of the corresponding columns. Make sure the box is checked for 'Labels in first row' in the ANOVA parameter window.
- Specify alpha in the ANOVA parameter window. Alpha represents the level of significance.
- Output the results into a new worksheet.
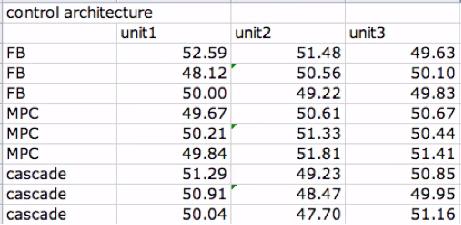
NOTE: Anova: Two Factor with Replication is used in the cases where there are multiple readings for a single factor. For instance, the input below, there are 2 factors, control architecture and unit. This input shows how there are 3 readings corresponding to each control architecture (FB, MPC, and cascade). In this sense, the control architecture is replicated 3 times, each time providing different data relating to each unit. So, in this case, you would want to use the Anova Two Factor with Replication option.
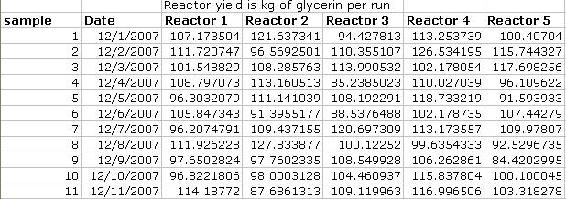
Anova: Two Factor without Replication is used in cases where there is only one reading pertaining to a particular factor. For example, in the case below, each sample (row) is independent of the other samples since they are based on the day they were taken. Since multiple readings were not taken within the same day, the "without Replication" option should be chosen.
Excel outputs:
Summary:
1. Count- number of data points in a set
2. Sum- sum of the data points in a set
3. Average- mean of the data points in a set
4. Variance- standard deviation of the data points in a set
ANOVA:
1. Sum of squares (SS)
2. The degree of freedom (df)
3. The mean squares (MS)
4. F-statistic (F)
5. P-value
6. Fcritical
See the figure below for an example of the inputs and outputs using Anova: Single Factor. Note the location of the Data Analysis tab. The data was obtained from the dieting programs described in Table 1. Since the F-statistic is greater than Fcritical, the null hypothesis can be rejected at a 95% confidence level (since alpha was set at 0.05). Thus, weight loss was not random and in fact depends on diet type chosen.

Determine the fouling rate of the reboiler at the following parameters:
- T = 410K
- Cc = 16.7g / L
- RT = 145min
Which process variable has the greatest effect (per unit) on the fouling rate of the reboiler?
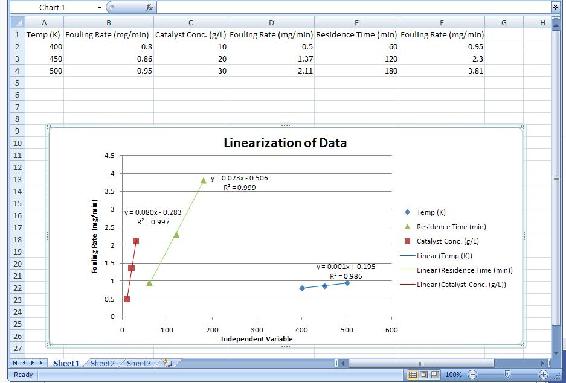
Note that the tables below are made up data. The output data for a single input was gathered assuming that the other input variables provide a negligible output. Although the factors that affect the fouling of the reboiler are similar to the ones found the the article linked in the "ANOVA and Factor Analysis in Process Controls" section, the data is not.
| Temperature of Reboiler (K) | 400 | 450 | 500 |
| Fouling Rate (mg/min) | 0.8 | 0.86 | 0.95 |
| Catalyst Concentration (g/L) | 10 | 20 | 30 |
| Fouling Rate (mg/min) | 0.5 | 1.37 | 2.11 |
| Residence Time (min) | 60 | 120 | 180 |
|---|---|---|---|
| Fouling Rate (mg/min) | 0.95 | 2.3 | 3.81 |
Solution
1) Determine the "factor loading" for each variable.
This can be done using any linearization tool. In this case, the factor loading is just the slope of the line for each set of data. Using Microsoft Excel, the equations for each set of data are the following:
Temperature of Reboiler
y = 0.0015 * x + 0.195
Factor loading: 0.0015
Catalyst Concentration
y = 0.0805 * x − 0.2833
Factor loading: 0.0805
Residence Time
y = 0.0238 * x − 0.5067
Factor loading: 0.0238
2) Determine the fouling rate for the given process conditions and which process variable affects the fouling rate the most (per unit). Note that the units of the factor loading value are always the units of the output divided by the units of the input.
Plug in the factor loading values into the following equation:
Output = f1 * input1 + f2 * input2 + ... + fn * inputn
You will end up with:
FoulingRate = 0.0015 * T + 0.0805 * Cc + 0.0238 * RT
Now plug in the process variables:
FoulingRate = 0.0015 * 410 + 0.0805 * 16.7 + 0.0238 * 145
FoulingRate = 5.41mg / min
The process variable that affects the fouling rate the most (per unit) is the catalyst concentration because it has the largest factor loading value.
The exit flow rate leaving a tank is being tested for 3 cases. The first case is under the normal operating conditions, while the second (A) and the third (B) cases are for new conditions that are being tested. The flow value of 7 (gallons /hour) is desired with a maximum of 10. A total of 24 runs are tested with 8 runs for each case. The tests are run to determine whether any of the new conditions will result in a more accurate flow rate. First, we determine if the new conditions A and B affect the flow rate. The results are as follows:
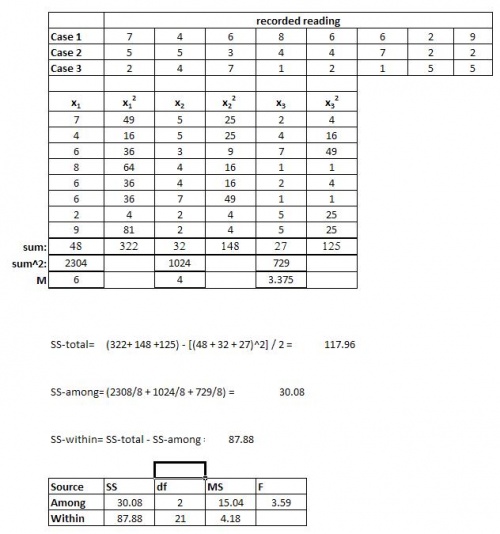
The recorded values for the 3 cases are tabulated. Following this the values for each case are squared and the sums for all of these are taken. For the 3 cases, the sums are squared and then their means are found.
These values are used to help determine the table above (the equations give an idea as to how they are calculated). In the same way with the help of ANOVA, these values can be determine faster. This can be done using the mathematica explained above.
Conclusion:
Fcritical equals 3.4668, from an F-table. Since the calculated F value is greater than Fcritical, we know that there is a statistically significant difference between 2 of the conditions. Thus, the null hypothesis can be rejected. However we do not know between which 2 conditions there is a difference. A post-hoc analysis will help us determine this. However we are able to confirmed that there is a difference.
As the new engineer on site, one of your assigned tasks is to install a new control architecture for three different units. You test three units in triplicate, each with 3 different control architecture: feedback (FB), model predictive control (MPC) and cascade control. In each case you measure the yield and organize the data as follows:
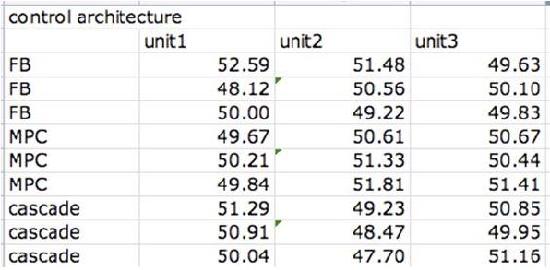
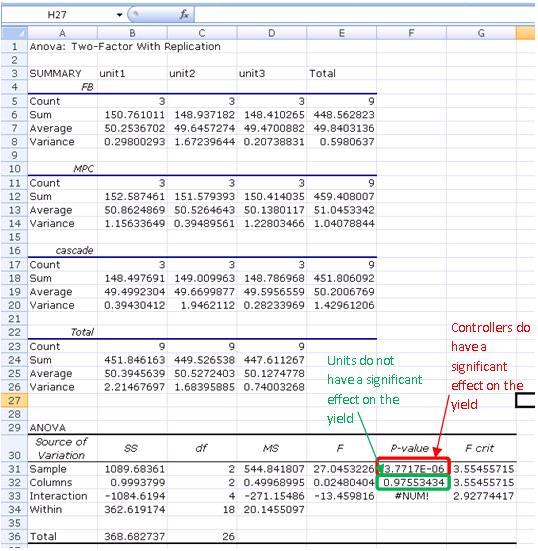
Do the units differ significantly? Do the control architectures differ significantly?
Solution
This problem can be solved using ANOVA Two factor with replication analysis.
ANOVA analysis works better for?
- Non-linear models
- Linear models
- Exponential models
- All of the above
- Answer
-
B
Two-Way ANOVA analysis is used to compare?
- Any two sets of data
- Two One-Way ANOVA models to each other
- Two factors on their effect of the output
- D. B and C
- Answer
-
C
References
- Ogunnaike, Babatunde and W. Harmon Ray. Process Dynamics, Modeling, and Control. Oxford University Press. New York, NY: 1994.
- Uts, J. and R. Hekerd. Mind on Statistics. Chapter 16 - Analysis of Variance. Belmont, CA: Brooks/Cole - Thomson Learning, Inc. 2004.
- Charles Spearman. Retrieved November 1, 2007, from www.indiana.edu/~intell/spearman.shtml
- Plonsky, M. "One Way ANOVA." Retrieved November 13, 2007, from www.uwsp.edu/psych/stat/12/anova-1w.htm
- Ender, Phil. "Statistical Tables F Distribution." Retrieved November 13, 2007, from www.gseis.ucla.edu/courses/help/dist3.html
- Devore, Jay L. Probability and Statistics for Engineering and the Sciences. Chapter 10 - The Analysis of Variance. Belment, CA: Brooks/Cole - Thomson Learning, Inc. 2004.
- "Mood's Median Test (Sign Scores Test)" Retrieved November 29, 2008, from www.micquality.com/six_sigma_glossary/mood_median_test.htm


