2.1: Definitions of Reaction Rate and Extent of Reactions

Learning Objectives

By the end of this section, you should be able to:

• Define Reaction rate and r eaction extent

Calculate the reaction rate for the reaction, the rate of formation of compounds and the reaction extent

Reaction Rate

A reaction rate shows the rates of production of a chemical species. It can also show the rate of consumption of a species; for example, a reactant. In general though, we want an overall common reaction rate to describe changes in a chemical system.

Let’s look at an example. Say we have reaction represented as: \(A + 2B → 3C + D\)

For this system reaction rate can be expressed as follows:

\[r = \frac{d[D]}{dt}\]

The reaction rate is represented by the letter “r” or the Greek letter upsilon “\(\upsilon\)”

NOTE: I will stick with r as upsilon looks like “\(\nu\)” which we will use to represent the stoichiometric coefficient

Above we have written the reaction rate as if a substance with a coefficient of 1 was reacting (or being produced). This is the typical form of an overall reaction rate describing a reaction.

Rearranging the above equation, we can find the rate of production/consumption for any species based on this overall reaction rate, note that stoichiometric coefficients are positive for products and negative for reactants:

\[r_{A}=\frac{d[A]}{dt}=-\nu_{A}×r=(-1)×r\]

\[r_{B}=\frac{d[B]}{dt}=-\nu_{B}×r=(-2)×r\]

\[r_{C}=\frac{d[C]}{dt}=\nu_{C}×r=3×r\]

\[r_{D}=\frac{d[D]}{dt}=\nu_{D}×r=1×r\]

The general equation for calculating the reaction rate:

General notation: J is used to denote any compound involved in the reaction.

\(r = \frac{1}{\nu}\frac{d[J]}{dt}\)

Reaction rate at a given time can also be found from the graph of concentration of components in a system vs. time:

Exercise: Calculating the Reaction Rate

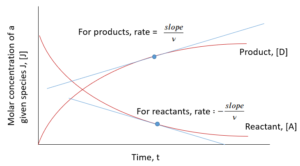
If we have the reaction

\[2 NOBr_{(g)} ⇌ 2 NO_{(g)} + Br_{2(g)}\]

and we measure that the rate of formation of NO is 1.6 mmol/(L·s), what are the overall reaction rate, and the rate of formation of \(Br_{2}\) and \(N\!O\!Br\)?

Solution

Add example text here.

Step 1: Determine the overall reaction rate from the rate of formation for NO.
\begin{align*}
r & = \frac{1}{\nu_{j}} \frac{d[NO]}{dt} \\
& = \frac{1}{2} \left( 1.6 \frac{mmol}{L·s}\right)\\
& = 0.8\frac{mmol}{L·s}
\end{align*}

Step 2: Use the reaction rate to determine rate of formation for the other compounds
NOTE: rate of formation is positive for products and negative for reactants
\begin{align*}
\frac{d[Br_{2}]}{dt}& = r \\
& = 0.8\frac{mmol}{L·s}
\end{align*}

\begin{align*}
\frac{d[NOBr]}{dt}& = -2r \\
& = -1.6\frac{mmol}{L·s}
\end{align*}

Reaction rates can be given in a variety of units over time. In this class we will just explore molarity and partial pressure, although other forms exist.

Molarity – molar concentration – expressed in units of \(\frac{mol}{volume * time}\) (eg. \(\frac{mol}{L*s}\) )

Partial pressure – the pressure produced by one gaseous component if it occupies the whole system volume at the same temperature, commonly used for gasses – units of \(\frac{pressure}{time}\)( eg. \(\frac{Pa}{s}\) )

Extent of Reaction

We use the extent of reaction (\(\xi\)) to describe the change in an amount of a reacting speicies J.

\(d n_{j} = \nu_{j} d\xi\)

where:

• \(dn_{j}\) = change in the number of moles of a certain substance
• \(\nu_{j}\) = the stoichiometric coefficient
• \(d\xi\) = the extent of reaction

We can get a relationship between the reaction extent and the rate of reaction when the system volume is constant:

\(r = \frac{1}{V} \frac{d\xi}{dt} = \frac{1}{\nu_{j}} \frac{1}{V} \frac{dn_{j}}{dt}\)

where:

\[V\]