1.7.1: Wetting of Surfaces
- Page ID
- 633
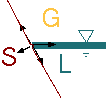
Fig. 1.21. Forces in contact angle.
To explain the source of the contact angle, consider the point where three phases became in contact. This contact point occurs due to free surface reaching a solid boundary. The surface tension occurs between gas phase (G) to liquid phase (L) and also occurs between the solid (S) and the liquid phases as well as between the gas phase and the solid phase. In Figure 1.21, forces diagram is shown when control volume is chosen so that the masses of the solid, liquid, and gas can be ignored. Regardless to the magnitude of the surface tensions (except to zero) the forces cannot be balanced for the description of straight lines. For example, forces balanced along the line of solid boundary is \[\sigma_{gs} - \sigma_{ls} - \sigma_{lg}\cos(\beta) = 0\] and in the tangent direction to the solid line the forces balance is \[F_{solid} = \sigma_{lg}\sin(\beta)\] Substituting equation (57) into equation (56) yields \[\sigma_{gs} - \sigma_{ls} = \frac{F_{solid}}{\tan(\beta)}\]

Fig. 1.22. Description of wetting and non-wetting fluids.
For \(\beta = \pi/2 \(=>) \tan(\beta) = \infty\). Thus, the solid reaction force must be zero. The gas solid surface tension is different from the liquid solid surface tension and hence violating equation (56).
The surface tension forces must be balanced, thus, a contact angle is created to balance it. The contact angle is determined by whether the surface tension between the gas solid (gs) is larger or smaller then the surface tension of liquid solid (ls) and the local geometry. It must be noted that the solid boundary isn't straight. The surface tension is a molecular phenomenon, thus depend on the locale structure of the surface and it provides the balance for these local structures.
The connection of the three phases–materials–mediums creates two situations which are categorized as wetting or non–wetting. There is a common definition of wetting the surface. If the angle of the contact between three materials is larger than \(90°\) then it is non–wetting. On the other hand, if the angle is below than \(90°\) the material is wetting the surface (see Fig. 1.22). The angle is determined by properties of the liquid, gas medium and the solid surface. And a small change on the solid surface can change the wetting condition to non–wetting. In fact there are commercial sprays that are intent to change the surface from wetting to non wetting. This fact is the reason that no reliable data can be provided with the exception to pure substances and perfect geometries. For example, water is described in many books as a wetting fluid. This statement is correct in most cases, however, when solid surface is made or cotted with certain materials, the water is changed to be wetting (for example 3M selling product to ``change'' water to non–wetting). So, the wetness of fluids is a function of the solid as well.
| Chemical Component | Contact Angle | Source |
| Steel | \(\pi/3.7\) | [1] |
| Steel, Nickel | \(\pi/4.74\) | [2] |
| Nickel | \(\pi/4.76\) to \(\pi/3.83\) | [1] |
| Nickel | \(\pi/4.76\) to \(\pi/3.83\) | [3] |
| Chrome-Nickel Steel | \(\pi/3.7\) | [4] |
| Silver | \(\pi/6\) to \(\pi/4.5\) | [5] |
| Zink | \(\pi/3.4\) | [4] |
| Bronze | \(\pi/3.2\) | [4] |
| Copper | \(\pi/4\) | [4] |
| Copper | \(\pi/3\) | [7] |
| Copper | \(\pi/2\) | [8] |
- R. Siegel, E. G. Keshock (1975) ``Effects of reduced gravity on nucleate boiling bubble dynamics in saturated water,'' AIChE Journal Volume 10 Issue 4, Pages 509 - 517. 1975
- Bergles A. E. and Rohsenow W. M. 'The determination of forced convection surface–boiling heat transfer, ASME, J. Heat Transfer, vol 1 pp 365 - 372.
- Tolubinsky, V.I. and Ostrovsky, Y.N. (1966) ``On the mechanism of boiling heat transfer'',. International Journal of Heat and Mass Transfer, Vol. 9, No 12, pages 1465-1470.
- Arefeva E.I., Aladev O, I.T., (1958) ``wlijanii smatchivaemosti na teploobmen pri kipenii,'' Injenerno Fizitcheskij Jurnal, 11-17 1(7) In Russian.
- Labuntsov D. A. (1939) ``Approximate theory of heat transfer by developed nucleate boiling'' In Sussian Izvestiya An SSSR , Energetika I transport, No 1.
- Basu, N., Warrier, G. R., and Dhir, V. K., (2002) ``Onset of Nucleate Boiling and Active Nucleation Site Density during Subcooled Flow Boiling,'' ASME Journal of Heat Transfer, Vol. 124, papes 717 -728.
- Gaetner, R. F., and Westwater, J. W., (1960) ``Population of Active Sites in Nucleate Boiling Heat Transfer,'' Chem. Eng. Prog. Symp., Ser. 56.
- Wang, C. H., and Dhir, V. K., (1993), ``Effect of Surface Wettability on Active Nucleation Site Density During Pool Boiling of Water on a Vertical Surface,'' J. Heat Transfer 115, pp. 659-669
To explain the contour of the surface, and the contact angle consider simple ``wetting'' liquid contacting a solid material in two–dimensional shape as depicted in Figure 1.23. To solve the shape of the liquid surface, the pressure difference between the two sides of free surface has to be balanced by the surface tension. In Figure 1.23, \(h\) describes the raising of the liquid as results of the surface tension. The surface tension
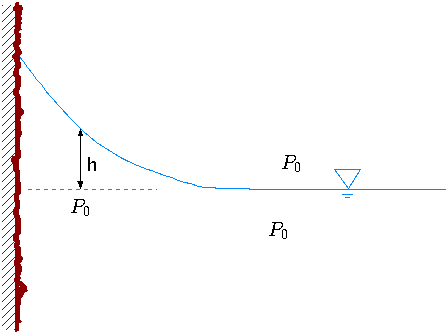
reduces the pressure in the liquid above the liquid line (the dotted line in the Figure 1.23). The pressure just below the surface is \( -gh(x)\rho\). The pressure, on the gas side, is the atmospheric pressure. This problem is a two dimensional problem and equation (49) is applicable to it. Applying equation (49) and using the pressure difference yields \[gh(x)\rho = \frac{\sigma}{R(x)}\] The radius of any continuous function, h = h(x), is \[R(x) = \frac{\left(1+[\dot{h}(x)]^{2}\right)^{3/2}}{\ddot{h}(x)}\] Where \(\dot{h}\) is the derivative of \(h\) with respect to \(x\).
Equation (60) can be derived either by forcing a circle at three points at (x, x+dx, and x+2dx) and thus finding the the diameter or by geometrical analysis of triangles build on points x and x+dx (perpendicular to the tangent at these points). Substituting equation (60) into equation (59) yields \[gh(x)\rho = \frac{\sigma}{\frac{\left(1+[\dot{h}(x)]^{2}\right)^{3/2}}{\ddot{h}(x)}}\] Equation (61) is non–linear differential equation for height and can be written as
1-D Surface Due to Surface Tension
\[\frac{gh\rho}{\sigma}\left(1 + \left[\frac{dh}{dx}\right]^{2}\right)^{3/2} - \frac{d^{2}h}{dx^{2}} = 0 \]
With the boundary conditions that specify either the derivative \(\dot{h}(x = r) = 0\) (symmetry) and the derivative at \(\dot{h}x=\beta\) or heights in two points or other combinations. An alternative presentation of equation (61) is \[gh\rho = \frac{\sigma\ddot{h}}{\left(1+\dot{h}^{2}\right)^{3/2}}\] Integrating equation (63) transforms into \[\int{\frac{g\rho}{\sigma}h}dh = \int{\frac{\ddot{h}}{\left(1+\dot{h}^{2}\right)^{3/2}}}dh\] The constant \(Lp = \sigma / \rho g\) is referred to as Laplace's capillarity constant. The units of this constant are meter squared. The differential \(dh\) is \(\dot{h}\). Using dummy variable and the identities \(\dot{h} = \xi\) and hence, \(\ddot{h} = \dot{\xi} = d\xi\) transforms equation (64) into \[\int{\frac{1}{Lp}hdh} = \int{\frac{\xi d\xi}{\left(1+\xi^{2}\right)^{3/2}}}\] After the integration equation (65) becomes \[\frac{h^{2}}{2Lp} + constant = -\frac{1}{\left(1+\dot{h}^{2}\right)^{1/2}}\] At infinity, the height and the derivative of the height must by zero so \(constant + 0 = -1/1\) and hence, \(constant = -1\). \[1 - \frac{h^{2}}{2Lp} = \frac{1}{\left(1+\dot{h}^{2}\right)^{1/2}}\] Equation (67) is a first order differential equation that can be solved by variables separation. Equation (67) can be rearranged to be \[\left(1+ \dot{h}^{2}\right)^{1/2} = \frac{1}{1 - \frac{h^{2}}{2Lp}}\] Squaring both sides and moving the one to the right side yields \[\dot{h}^{2} = \left(\frac{1}{1 - \frac{h^{2}}{2Lp}}\right)^{2} - 1 \] The last stage of the separation is taking the square root of both sides to be \[\dot{h} = \frac{dh}{dx} = \sqrt{\left(\frac{1}{1 - \frac{h^{2}}{2Lp}}\right)^{2} - 1} \] or \[\frac{dh}{\sqrt{\left(\frac{1}{1 - \frac{h^{2}}{2Lp}}\right)^{2} - 1}} = dx \] Equation (71) can be integrated to yield \[\int{\frac{dh}{\sqrt{\left(\frac{1}{1 - \frac{h^{2}}{2Lp}}\right)^{2} - 1}}} = x + constant \] The constant is determined by the boundary condition at \(x = 0\). For example if \(h(x - 0) = h_{0}\) then \(cosntant = h_{0}\). This equation is studied extensively in classes on surface tension. Furthermore, this equation describes the dimensionless parameter that affects this phenomenon and this parameter will be studied further at another time. This book is introductory, therefore this discussion on surface tension equation will be limited.


