5.2: Px and Tx Diagrams
- Page ID
- 7497
In addition to considering variations with pressure, temperature, and volume, as we have done so far, it is also very constructive to consider variations with composition. Most literature on the subject calls these diagrams the “P-x” and “T-x” diagrams respectively. However, a word of caution is needed in order not to confuse the reader. Even though “x” stands for “composition” — in a general sense — here, we will see in the next section that it is also customary to use “x” to single out the composition of the liquid phase. In fact, when we are dealing with a mixture of liquid and vapor, it is customary to refer to the composition of the liquid phase as “xi” and use “yi” for the composition of the vapor phase. “xi” pertains to the amount of component in the liquid phase per mole of liquid phase, and “yi” pertains to the amount of component in the vapor phase per mole of vapor phase. However, when we talk about composition in general, we are really talking about the overall composition of the mixture, the one that identifies the amount of component per unit mole of mixture. It is more convenient to call this overall composition “zi”. If we do so, these series of diagram should be called “P-z” and “T-z” diagrams. This is a little awkward in terms of traditional usage; and hence, we call them “P-x” and “T-x” where “x” here refers to overall composition as opposed to liquid composition.
A P-x diagram for a binary system at constant temperature and a T-x diagram for a binary system at a constant pressure are displayed in Figures 5.2.3 and 5.2.4, respectively. The lines shown on the figures represent the bubble and dew point curves. Note that the end points represent the pure-component boiling points for substances A and B.
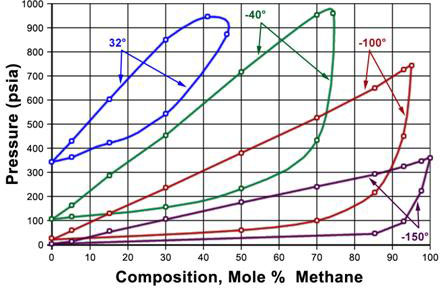
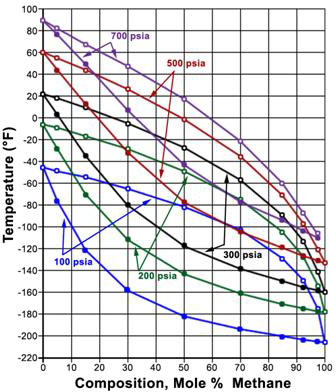
Figure \(\PageIndex{4}\): T-X Diagram For Binary System
(Courtesy of ©LOMIC, INC)
In a P-x diagram (Figure 5.2.3), the bubble point and dew point curves bound the two-phase region at its top and its bottom, respectively. The single-phase liquid region is found at high pressures; the single-phase vapor region is found at low pressures. In the T-x diagram (Figure 5.2.4), this happens in the reverse order; vapor is found at high temperatures and liquid at low temperatures. Consequently, the bubble point and dew point curve are found at the bottom and the top of the two-phase region, respectively.


