Real and Reciprocal Crystal Lattices
- Page ID
- 318
Crystal is a three dimensional periodic array of atoms. Crystal lattice is the geometrical pattern of the crystal, where all the atom sites are represented by the geometrical points. There are two classes of crystal lattices. When all of the lattice points are equivalent, it is called Bravais lattice. Otherwise, it is called non-Bravais lattice. The non-Bravais lattice may be regarded as a combination of two or more interpenetrating Bravais lattices with fixed orientations relative to each other.
The crystal lattice can also be defined by three fundamental translation vectors: \(a_{1}\), \(a_{2}\), \(a_{3}\). When, \(r=r_{1}+n_{1}a_{1}+n_{2}a_{2}+n_{3}a_{3}\), (n1, n2, n3 are arbitrary integers.), The whole crystal looks the same in every respect when viewed from \(r\) and \(r_{1}\). Additionally, if any two points have the relation of \(r\) and \(r_{1}\), when a proper set of \(n_1\), \(n_2\), \(n_3\) is chosen, \(a_{1}\), \(a_{2}\), \(a_{3}\) are said to be the primitive vector, and they can form the primitive unit cell.
Primitive cell has the smallest volume. The volume of the nonprimitive unit cell is an integral multiple of the primitive unit cell. The choice of primitive unit cell is not unique, and there are many ways of forming a primitive unit cell. One way of choosing a unit cell is shown in Figure \(\PageIndex{1}\). The procedure is:
- draw lines to connect a given lattice points to all nearby lattice points;
- at the midpoint and normal to these lines, draw new lines or planes.
The smallest volume enclosed in this way is a primitive unit cell, and also called the Wigner-Seitz primitive cell.
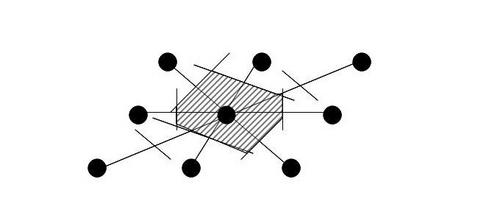
Figure \(\PageIndex{1}\) Procedure to create a Wigner-Seitz primitive cell.
2. Fundamental types of crystal lattices
Because of the translational symmetry of the crystal lattice, the number of the types of the Bravais lattices can be reduced to 14, which can be further grouped into 7 crystal system: triclinic, monoclinic, orthorhombic, tetragonal, cubic, hexagonal, and the trigonal (rhombohedral). Figure \(\PageIndex{2}\) shows all of the Bravais lattice types.
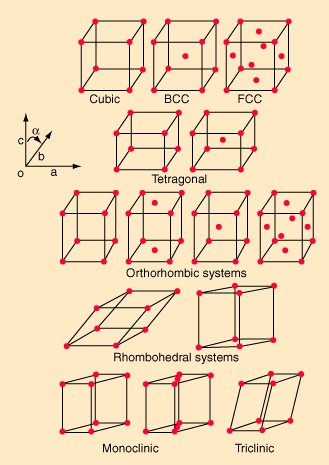
Figure \(\PageIndex{2}\) 14 Bravais lattices and 7 crystal systems
These 14 lattice types can cover all possible Bravais lattices. All other lattices shape must be identical to one of the lattice types listed in Figure \(\PageIndex{2}\). For example, a base centered tetragonal is identical to a simple tetragonal cell by choosing a proper unit cell. As shown in Figure \(\PageIndex{3}\), connect two base centered tetragonal lattices, and choose the shaded area as the new unit cell. It is found that the base centered tetragonal cell is identical to the simple tetragonal cell. It is mathematically proved that he lattice types listed in Figure \(\PageIndex{2}\) is a complete lattice type.
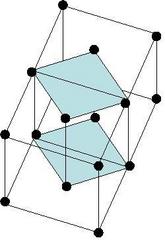
3. Fundamental Types of Symmetry Properties
Crystal lattices are periodic structures, they have one or more types of symmetry properties, such as inversion, reflection, rotation. Table \(\PageIndex{1}\) summarized the characteristic symmetry elements of the 7 crystal system.
Inversion: If the cell remains the same after the mathematical transformation performance of \(\mathbf{r}\) and –\(\mathbf{r}\), it has inversion symmetry. All Bravais lattices have inversion symmetry.
Reflection: If the cell remains the same after a mirror reflection is performed on it, it has reflection symmetry.
Rotation axis: If the cell remains the same after it rotates around an axis with some angle, it has the rotation symmetry, and the axis is call n-fold, when the angle of rotation is \(2\pi /n\).
| Crystal system | Reflection plane | Rotation axis |
|---|---|---|
| Triclinic | None | None |
| Monoclinic | 1 | 1 2-fold |
| Orthorhombic | None | 3 2-fold |
| Tetragonal | None | 1 4-fold |
| Cubic | 9 | 4 3-fold |
| Trigonal | None | 1 3-fold |
| Hexagonal | None | 1 3-fold |
A non-Bravais lattice is the lattice with each site associated with a cluster of atoms called basis. Therefore the description of symmetry of a non-Bravais lattice includes the symmetry of the basis and the symmetry of the Bravais lattice on which this basis is imposed. The symmetry of the basis is called point-group symmetry. Because of the requirements of translational symmetry for the lattice as a whole, there are totally 32 types of the point group symmetry.
Additionally, the rotation symmetry of the basis is essentially the same as the rotation symmetry of the Bravais lattice, which has 14 types. Combination the rotation symmetry of the point groups with the translational symmetry, 72 space groups are generated. As for the space groups involve symmetry elements such as screw axes, glide planes, etc., they can not be the simple sum of point group and space group. With the consideration of this, 230 space groups are obtained.
4. Crystal directions, Crystal Planes and Miller Indices
Index of the crystal planes can be determined in the following ways, as also illustrated in Figure \(\PageIndex{4}\).
- Determine the axes, such as \(a_{1}\), \(a_{2}\), \(a_{3}\) in Figure \(\PageIndex{4}\).
- Find the interception of the plane on the axes in terms of the axes constant, which is (3, 3, 2) in Figure \(\PageIndex{4}\).
- Take the reciprocals and reduce them to the smallest integers, the index of the plane with blue color is determined to be (2, 2, 3).
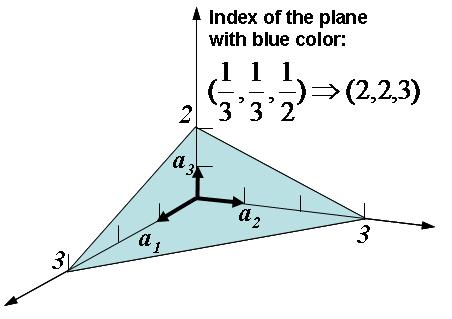
Figure \(\PageIndex{4}\) Determination of the crystal plane index
5. Reciprocal Lattices
Every crystal structure has two lattices associated with it, the crystal lattice and the reciprocal lattice. A diffraction pattern of a crystal is the map of the reciprocal lattice of the crystal and a microscope structure is the map of the crystal structure. If \(a_{1}\), \(a_{2}\), \(a_{3}\) are the axis vectors of the real lattice, and \(b_{1}\), \(b_{2}\), \(b_{3}\) are the axis vectors of the reciprocal lattice, they are related by the following equations:
\[\begin{align} \rm b_{1}=2\pi\frac{\rm a_{2}\times\rm a_{3}}{\rm a_{1}\ast\rm a_{2}\times\rm a_{3}} \end{align} \label{1}\]
\[ \begin{align} \rm b_{2}=2\pi\frac{\rm a_{3}\times\rm a_{1}}{\rm a_{1}\ast\rm a_{2}\times\rm a_{3}} \end{align} \label{2}\]
\[ \begin{align} \rm b_{3}=2\pi\frac{\rm a_{1}\times\rm a_{2}}{\rm a_{1}\ast\rm a_{2}\times\rm a_{3}} \end{align} \label{3}\]
Using \(b_{1}\), \(b_{2}\), \(b_{3}\) as a basis for a new lattice, then the vectors are given by
\[\begin{align} \rm G=\rm n_{1}\rm b_{1}+\rm n_{2}\rm b_{2}+\rm n_{3}\rm b_{3} \end{align} \label{4}\]
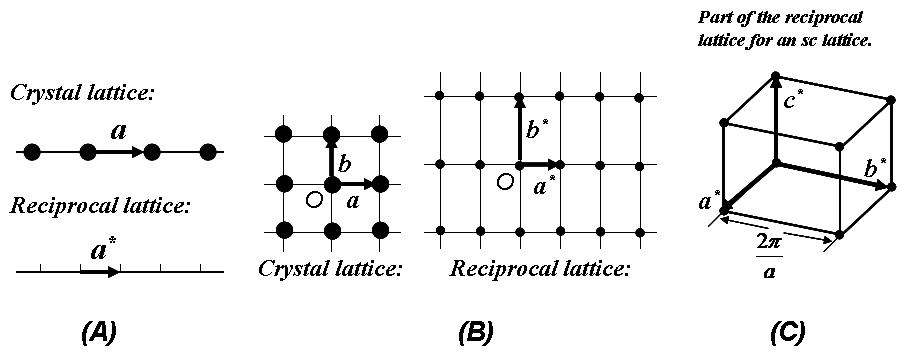
Figure \(\PageIndex{5}\) (a). Reciprocal lattice for a 1-D crystal lattice; (b). Reciprocal lattice for a 2-D crystal lattice; (c). Part of the reciprocal lattice for an sc lattice.
Based on the definition of the reciprocal lattice, the vectors of the reciprocal lattice \(G_{hkl}=\rm h\rm b_{1}+\rm k\rm b_{2}+\rm l\rm b_{3}\) can be related the crystal planes of the direct lattice \((hkl)\):
(a) The vector \(G_{hkl}\) is normal to the (hkl) crystal planes.
(b) The interplane distance \(d_{hkl}\) is related to the magnitude of \(G_{hkl}\) by
\[\begin{align} \rm d_{hkl}=\frac{2\pi}{\rm G_{hkl}} \end{align} \label{5}\]
The vector \(G_{hkl}\) is normal to the crystal planes (hkl). And the separation of these planes is \(2\pi\) times the inverse of the length \(G_{hkl}\) in the reciprocal space.
Reference
- C. Kittel, in Introduction to Solid State Physics, edited by John Wiley, New York, 1996, pp. 1-52.
- M. A. Omar, in Elementary Solid State Physics, edited by Pearson education Inc., pp. 2-33.
Contributors and Attributions
ContribMSE5317

