Resistivity
- Page ID
- 324
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Resistivity is the material property that pertains to how difficult it is for electrical current to flow through said material. Materials with high resistivity are known as insulators while materials with low resistivity are known as conductors. Spanning from 10-8 Ωm to 1020 Ωm (see Figure \(\PageIndex{1}\)), resistivity possess the largest range of values for any physical property. Resistivity is essential in many material applications including resistors in electrical circuits, dielectrics, resistive heating, and superconducting.

Introduction
The fundamental relationship that explores a materials opposition to electron flow was first derived in 1826 by Georg Ohm, a German physicist and mathematician. Ohm's Law is represented by the following equation:
\[V=IR\nonumber\]
where
- V [Volts: J/C] is the voltage applied to the material,
- I [Amperes: C/s] is the electrical current flow, and
- R [ohms: V/A] is the resistance of the material specimen.
It is important to note that resistance is dependent on the specific geometry of a material specimen as seen in Figure 2.

To represent the electrical resistivity as an intrinsic material property, the voltage must be divided by the length L at which it is applied to and the current must be divided by the area A it flows through to produce an electric field \(\xi\) and current density J respectively. This translation to electric field and current density yields the following equation for resistivity: \[ρ=\dfrac{\xi}{J}\nonumber\]
where \(\rho\) is the resistivity of a material \([\Omega m]\). When comparing materials, it is common to invert the value of resistivity to make conductivity \(\sigma\) [Siemens] which can easily be used to rank materials on the basis of how well each conducts electrons. Due to the significant temperature dependence on resistivity and conductivity, a material's resistiveness measured at room temperature [20°C].
As mentioned above, materials are broken into three essential regimes: insulators, semiconductors, and metals. The manifestation of resistivity in conducting materials, metals and semiconductors, can be fully realized by evaluating the behavior of electrons at the quantum mechanical level.
Resistivity of Pure Metals
Metals are structured by a lattice of atoms that are metallically bonded to one another. The sea of delocalized electrons found in metallic bonding is created by having a high density of states (i.e. electrons) at the Fermi level which are easily excited into the conduction band. From this bonding, electrons a can be thought of as free electrons moving through the metal matrix. As the electron flows, it will interact with individual atoms, causing scattering events, which decrease the effectiveness of electrons at traversing the metal. The mobility of the electrons play an important role in quantifying the resistivity of a metal as seen in the following equation:
\[\rho=\dfrac{3}{e^2 v_f^2 TN(E_f)}\nonumber\]
where e is the charge of an electron, \(V_F\) Fermi velocity of a conduction electron, τ is the relaxation time between scattering events, and \(N(E_F)\) is the population density of electrons at the Fermi energy. Additionally, it is seen that the population density of electrons at the Fermi level is taken in to account as opposed to the total number of valance electrons, which explains the exceptionally low resistivity of silver, copper and gold.
Temperature Dependence
The equation above shows that the resistivity of a metal is inversely proportionally to the relaxation time. This means the number of scattering events plays a substantial role in the resistivity of a metal. A large contributor to the number of scattering events iin a metal is the thermal vibrations of each atom in the lattice. As the temperature of a material increases, each atom beings to oscillate about its central position, increasing the probability that an electron would collide with it. This relationship is visualized by measuring the resistivity of silver as a function of temperature, Figure \(\PageIndex{3}\).

Metals exhibit a minimal resistivity at temperatures approaching 0 Kelvin, known as a residual resistivity, and a linear increase in resistivity as the metal reaches its melting point.
Residual Resistivity and Matthiessen's Rule
At low enough temperatures, the degrees of thermal vibration are not yet activated meaning the residual resistivity of a metal is a collection of all other scattering sites present in the material specifically defects and impurities. With polycrystalline metals, there will be a number of sources of defects in the microstructure including Grain boundaries, dislocations, and vacancies. Along with defects, impurities in a metal can host a scattering site. In 1864 Augustus Matthiessen, a British chemist and physicist, was the first to incorporate all of these aspects into the resistivity of a metal. Matthiessen's Rule is as follows:
\[\rho=\rho_{th}+\rho_{imp}+\rho_{def}\nonumber\]
where \(\rho_{th}\) is the resistivity due to temperature, \(\rho_{imp}\) is the resistivity due to impurities and \(\rho_{def}\) is the the resistivity due to defects. While temperature, defects, and impurities do in fact contribute to resistivity, some deviation from the simple summation postulated by Matthiessen has been reported for specific metals.
Resistivity of Alloys
From Matthiessen's Rule it was seen that the resistivity of a metal was influenced by the impurities present. This portion of the resistivity begins to have a significant contribution when metals are alloyed together. An alloy can be viewed as a metal with a large number of impurities, meaning there is a great deal more scattering sites to increase the residual resistivity of the metal. The result of this increase is a translation of the plot in Figure \(\PageIndex{3}\) upward. At varying compositions of a simple binary alloy, the resistivity of the system is a linear interpolation of the resistivity of each pure metal. If the system exhibits an energetically favorable phase transition that results in a more ordered structure than that of the solute atoms in solution, a drop in resistivity at that composition will be observed. An example of a binary system that has ordered phases that affect resistivity is copper and platinum.
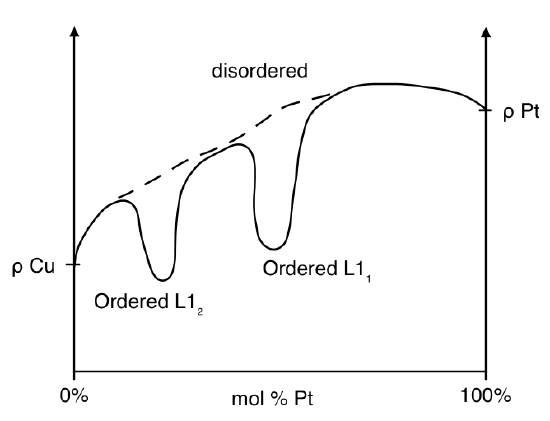
The plot of the copper platinum binary system demonstrates the result of the ordered phases \(L_2\) and \(L_1\). Similar to the deviations from Matthiessen's Rule, formulation of the relationship of resistivity of any alloy has not been adequately developed because of the complexity of the structures created by any given alloy system. Several rules have been created with little implication because each emphasizes a specific subset of alloys with particular characteristics.
Resistivity of Semiconductors
The primary distinguishing factor between metals and any other material is that metals do not possess a band gap or a range of energy levels that are not allowed for electrons to inhabit. It has been observed that the size of the band gap of a material how insulative it is and at low enough band gaps, the material can be partially conductive. These materials are, of course, semiconductors. Similar to metals, through band theory, the following relationship can be determined for the resistivity of a semiconductor.
\[\rho=\dfrac{m_e*}{e^2\tau_eN_e}+\dfrac{m_h*}{e^2\tau_hN_h}\nonumber\]
where \(m_e^{\ast}\) and \(m_{h}^{\ast}\) are the effective masses of electrons and holes respectively, \(N_e\) and \(N_h\) are the number of electrons and holes respectively, and \(T_e\) and \(T_h\) are the relaxation times for electrons and hole respectively. Acknowledging the inverse dependence of the number of both electrons and holes on the resistivity, extrinsic semiconductors would be expected to have a lower resistivity due to there addition of more charge carriers.
Temperature Dependence
The temperature dependence of semiconductors act very different to metals. With the band gap limiting the excitation of electrons to the conduction band, energy must be supplied to the semiconductor to decrease the resistivity. This energy is supplied thermally, and corresponds to the band gap energy.
\[\rho=\rho_0 exp(\dfrac{-E_g}{2kT})\nonumber\]
where \(\rho_0\) is the resistivity of the semiconductor as determined from the equation above, \(E_g\) is the band gap energy, \(k\) is the Boltzmann's constant and \(T\) is the temperature.
For intrinsic semiconductors, that contain equal numbers of electron and holes, the temperature dependence resolves the trend seen in Figure \(\PageIndex{5}\). From Figure \(\PageIndex{5}\), the promotion of more electrons at higher temperatures is observed as well as a freeze out region at low temperatures where no charge carrying species are excited to the conduction band.

As is expected, extrinsic semiconductors exhibit a similar temperature dependence to their intrinsic counterparts with the small deviation during a portion of the temperature range.
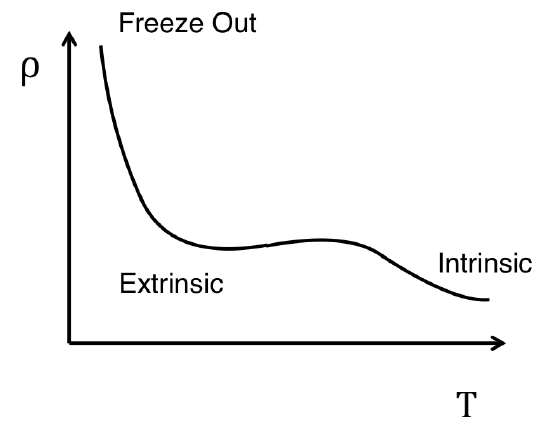
For a temperature range in the middle of Figure \(\PageIndex{6}\), the resistivity remained relatively constant while the material heats. This accounts for the additional charge carriers found in extrinsic semiconductors that have already decreased the resistivity of the semiconductor below the value for the intrinsic counterpart. During the region of temperatures when the resistivity is not changing, the number of electrons being thermally excited to the conduction band is not yet large enough to influence the resistivity as much as the extrinsic doping has. Eventually the number of excited electrons becomes great enough to resume the intrinsic temperature dependent trend.
Questions
- What distinguishes resistance from resistivity? Why is it important to quantify resistivity?
- According to Matthiessen's Rule, what contributes to the residual resistivity of a metal?
- Calculate the resistance through a rectangular wafer of Germanium at 350°C. Dimensions: width= 3cm thickness= 5mm length= 15cm. Resistivity at room temperature: 1 Ωm Band Gap energy: 0.67 eV
Answers
- Resistance is a value specific to the particular specimen geometry of the material while resistivity does not depend on geometry. It is important to refer to resistivity when comparing materials because it is an intrinsic property.
- According to Matthiessen's Rule, residual resistivity is accounts for the resistivity brought upon by impurities and defects, specifically grain boundaries, dislocations, and vacancies, in the material.
- R=1.95 Ω at 350°C
References
- W. D. Callister and D. G. Rethwisch, "Materials Science and Engineering an Introduction," textbook, 8th Edition, Wiley, (2010).
- L. Solymar and D. Walsh, "Electrical Properties of Materials," textbook, 7thEdition, Oxford Press, (2004).
- R. E. Hummel, “Electronic Properties of Materials,” textbook, 4th Edition, Springer, (2011).
Contributors
- Benjamin MacDonald (B.S. Materials Science and Engineering, Class of 2015, University of California, Davis)

