Compton Effect
- Page ID
- 310
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Compton effect (also called Compton scattering) is the result of a high-energy photon colliding with a target, which releases loosely bound electrons from the outer shell of the atom or molecule. The scattered radiation experiences a wavelength shift that cannot be explained in terms of classical wave theory, thus lending support to Einstein's photon theory. The effect was first demonstrated in 1923 by Arthur Holly Compton (for which he received a 1927 Nobel Prize). The effect is important because it demonstrates that light cannot be explained purely as a wave phenomenon. Thomson scattering, the classical theory of an electromagnetic wave scattered by charged particles, cannot explain low intensity shift in wavelength. Classically, light of sufficient intensity for the electric field to accelerate a charged particle to a relativistic speed will cause radiation-pressure recoil and an associated Doppler shift of the scattered light, but the effect would become arbitrarily small at sufficiently low light intensities regardless of wavelength. Light must behave as if it consists of particles in order to explain the low-intensity Compton scattering. Compton's experiment convinced physicists that light can behave as a stream of particles whose energy is proportional to the frequency.
The experiment
A schematic diagram of the apparatus used by Compton is shown in the Figure below. A graphite target was bombarded with monochromatic x-rays and the wavelength of the scattered radiation was measured with a rotating crystal spectrometer. The intensity was determined by a movable ionization chamber that generated a current proportional to the x-ray intensity. Compton measured the dependence of scattered x-ray intensity on wavelength at three different scattering angles of 45o 90o ,and 135o
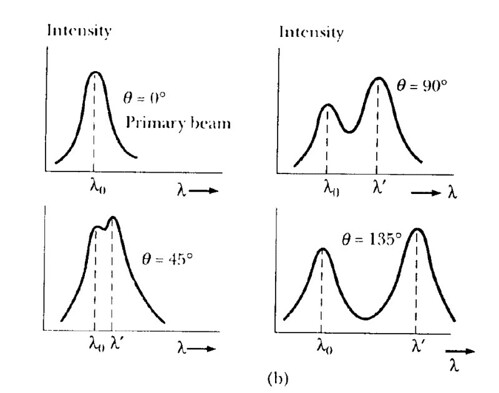
Physics
Compton effect is the decrease in energy (increase in wavelength) of an X-ray or gamma ray photon, when it interacts with matter. Because of the change in photon energy, it is an inelastic scattering process. Inverse Compton scattering also exists, where the photon gains energy (decreasing in wavelength) upon interaction with matter. Compton used a combination of three fundamental formulas representing the various aspects of classical and modern physics, combining them to describe the quantum behavior of light:
- Light as a particle, as noted in the photoelectric effect
- Relativistic dynamics: special theory of relativity
- Trigonometry: law of cosines
We can think of the photon as losing an amount of energy in the collision that is the same as the kinetic energy (KE) gained by the electron, although actually separate photons are involved. If the initial photon has the frequency \(\nu\) associated with it, the scattered photon has the lower frequency \(\nu'\), where
Loss in photon energy = gain in electron energy
\[h\nu-h\nu'=KE \label{1}\]
and the momentum of a massless particle is related to its energy by the formula
\[ E=pc \label{2}\]
since the energy of a photon is \(h\nu\), its momentum is
\[ p=\dfrac{E}{c}=\dfrac{h\nu}{c} \label{3}\]
Momentum, unlike energy is a vector quantity that incorporates direction as well as magnitude, and in the collision momentum must be conserved in each of two mutually perpendicular directions (when more than two bodies participate in a collision, momentum must be conserved in each of three mutually perpendicular directions). The directions we choose here are that of the original photon and one perpendicular to it in the plane containing the electron and the scattered photon (Figure \(\PageIndex{2}\)).

Figure \(\PageIndex{2}\) The initial photon momentum is \(h\nu/c\), the scattered photon momentum is \(h\nu '/c\), and the initial and final electron momenta are respectively 0 and p. In the original photon direction
Initial momentum = final momentum
\[ h\nu/c+0=(h\nu'/c)\cos \theta+p\cos\phi \label{4}\]
and perpendicular to this direction
Initial momentum= final momentum
\[ 0=(h\nu'/c)\sin\theta-p\sin\phi \label{5}\]
From Equation (1)(4)(5), we can find a formula that relates the wavelength difference between initial and scattered photons with the angle \(\theta\) between their directions, both of which are readily measurable quantities (unlike the energy and momentum of the recoil electron).
The first step is to multiply Eqs (4)(5) by c adn rewrite them as
\[ (pc)\cos\phi=h\nu-(h\nu')\cos\theta \label{6}\]
\[ (pc)\sin\phi=(h\nu')\sin\theta \label{7}\]
By squaring each of these equations and adding the new ones together, the angle \(\phi\) is eliminated, leaving
\[ p^2c^2=(h\nu)^2-2(h\nu)(h\nu')\cos\theta+(h\nu')^2 \label{8}\]
Next we equate the two expressions for the total energy of a particle
\[ E=KE+mc^2 \label{9}\]
From equation(1), we have
\[ p^2c^2=(h\nu)^2-2(h\nu)(h\nu')+(h\nu')^2+2mc^2(h\nu-h\nu') \label{11}\]
Substituting this value of \(p^2c^2\) in Eq.(8), we finally obtain
\[ 2mc^2(h\nu-h\nu')=2(h\nu)(h\nu')(1-\cos\theta) \label{12}\]
This relationship is simpler when expressed in terms of wavelength \(\lambda\).Dividing Eq.(12) by \(2h^2c^2\),
\[ mc/h(\nu/c-\nu'/c)=(\nu/c)(\nu'/c)(1-\cos\theta) \label{13}\]
and so, since \(\nu/c=1/\lambda\) and \(\nu'/c=1/\lambda'\)
\[ mc/h(1/\lambda-1/\lambda')=(1-\cos\theta)/\lambda\lambda' \label{14}\]
\[ \lambda-\lambda'=h/mc(1-\cos\theta) \label{15}\]
Equation(15) gives the change in wavelength expected for a photon that is scattered through the angle \(\theta\) by a particle mass \(m\). This change is independent of the wavelength \(\lambda\) of incident photon. The quantity
\[ \lambda_{^{_{c}}}=\dfrac{h}{mc} \label{16}\]
is called the Compton wavelength of the scattering particle. For an electron \(\lambda_c=2.426 \times 10^{-12}\;m\). In terms of \(\lambda_c\), Eq.(15) becomes
\[ \lambda-\lambda'=\lambda_{^{_{c}}}(1-\cos \theta) \label{17}\]
The Compton wavelength gives the scale of the wavelength change of the incident photon. From Eq.(17) we note that the greatest wavelength change possible corresponds to \(\theta =180^o\), when the wavelength change will be twice the Compton wavelength \(\lambda_c\). Because \(\lambda_c= 0.00243\; nm\) for an electron, and even less for other particles owing to their larger rest masses, the maximum wavelength change in the Compton effect is 0.004852 nm.
Figure \(\PageIndex{3}\) If the photon is of lower energy, but still has sufficient energy (in general a few eV, right around the energy of visible light), it can eject an electron from its host atom entirely (a process known as the photoelectric effect), instead of undergoing Compton scattering. Higher energy photons (~MeV) may be able to bombard the nucleus and cause an electron and a positron to be formed, a process called pair production
Applications
Compton scattering is of prime importance to radiobiology, as it happens to be the most probable interaction of high energy X rays with atomic nuclei in living beings and is applied in radiation therapy. In material physics, Compton scattering can be used to probe the wave function of the electrons in matter in the momentum representation. Compton scattering is an important effect in gamma spectroscopy which gives rise to the Compton edge, as it is possible for the gamma rays to scatter out of the detectors used. Compton suppression is used to detect stray scatter gamma rays to counteract this effect.
References
- http://en.Wikipedia.org/wiki/Compton_scattering
- A. Beiser. “ Concepts of Modern Physics 6th edition ” p. 75-79 (ISBN 007-123460-8)
- http://faculty.gvsu.edu/majumdak/public_html/OnlineMaterials/ModPhys/QM/QM1.htm
- http://physics.about.com/od/quantump...ptoneffect.htm
- forums.phys.unsw.edu.au/main/viewtopic.php?t=871
- http://hyperphysics.phy-astr.gsu.edu/hbase/atmos/blusky.html#c2
Contributors and Attributions
ContribMSE5317

