1.17: Momentum and Energy
- Page ID
- 50118
Two key experiments revolutionized science at the turn of the 20th century. Both experiments involve the interaction of light and electrons. We have already seen that electrons are best described by wavepackets. Similarly, light is carried by a wavepacket called a photon. The first phenomenon, the photoelectric effect, was explained by assuming that a photon‟s energy is proportional to its frequency. The second phenomenon, the Compton effect, was explained by proposing that photons carry momentum. That light should possess particle properties such as momentum was completely unexpected prior to the advent of quantum mechanics.
The Photoelectric Effect
It is not easy to pull electrons out of a solid. They are bound by their attraction to positive nuclei. But if we give an electron in a solid enough energy, we can overcome the binding energy and liberate an electron. The minimum energy required is known as the work function, W.
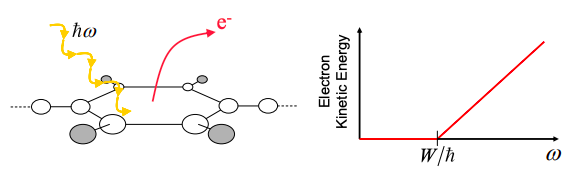
By bombarding metal surfaces with light, it was observed that electrons could be liberated only if the frequency of the light exceeded a critical value. Above the minimum frequency, electrons were liberated with greater kinetic energy.
Einstein explained the photoelectric effect by postulating that, in a photon, the energy was proportional to the frequency:
\[ E = \hbar\omega \nonumber \]
Where \(h = 6.62 \times 10^{-34} Js\) is Planck‟s constant, and is shorthand for \(\hbar=h/2\pi\). Note the units for Planck's constant – energy × time. This is useful to remember when checking that your quantum calculations make sense.
Thus, the kinetic energy of the emitted electrons is given by
\[ \text{electron kinetic energy} = \hbar\omega-W \nonumber \]
This technique is still used to probe the energy structure of materials
Note that we will typically express the energy of electrons in "electron Volts (eV)‟. The SI unit for energy, the Joule, is typically much too large for convenient discussion of electron energies. A more convenient unit is the energy required to move a single electron through a potential difference of 1V. Thus, \(1\ eV = q\ J\), where q is the charge on an electron (\(q \sim 1.602\times 10^{-19}\ C\)).
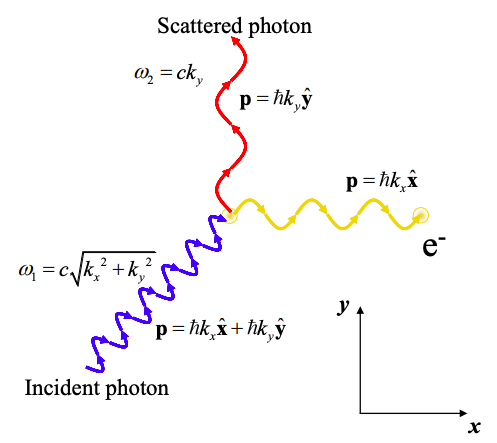
The Compton Effect
If a photon collides with an electron, the wavelength and trajectory of the photon is observed to change. After the collision the scattered photon is red shifted, i.e. its frequency is reduced and its wavelength extended. The trajectory and wavelength of the photon can be calculated by assuming that the photon carries momentum:
\[ p = \hbar k \nonumber \]
where the wavenumber k is related to frequency by
\[ k = \frac{2\pi}{\lambda} = \frac{\omega}{c} \nonumber \]
where c is the speed of light.
These two relations: \(E=\hbar \omega\) and \(p=\hbar k\) are strictly true only for plane waves with precisely defined values of ω and k. Otherwise we must employ operators for momentum and energy. Based on the operators we defined earlier for k and ω, we define operators for momentum
\[ \hat{p} = -i\hbar \frac{d}{dx} \nonumber \]
and energy
\[ \hat{E} = i\hbar \frac{d}{dt} \nonumber \]
Recall that each operator acts on the function to its right; and that \(\hat{p}\psi\) is not necessarily equal to \(\psi \hat{p}\).


